本文主要是介绍【动态规划】24子数组系列_最长湍流子数组_C++,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
题目链接:最长湍流子数组
目录
题目解析:
算法原理
1.状态表示
2.状态转移方程
3.初始化
4.填表顺序
5.返回值
编写代码
题目解析:

题目让我们求返回 arr 的 最大湍流子数组的长度
由题可得:
如果比较符号在子数组中的每个相邻元素对之间翻转,则该子数组是 湍流子数组;
算法原理:
1.状态表示
先创建一个dp表
首先先思考dp表里面的值所表示的含义(是什么?)
这里我们需要两个dp表:
f[i]:以i位置为结尾,i位置为“上升”的最大湍流子数组的长度
g[i]:以i位置为结尾,i位置为“下降”的最大湍流子数组的长度
这种状态表示怎么来的?
1.经验+题目要求
用之前或者之后的状态,推导出dp[i][j]的值;
根据最近的最近的一步,来划分问题
经验:以i位置为结尾;
题目让我们返回 arr 的 最大湍流子数组的长度 ,
所以我们可以先设一个“dp表”表示以i位置为结尾,i位置最大湍流子数组的长度。
但是我们会发现:
只有一个dp表无法表示该位置的状态,状态分得还不够细(是>还是<)
所以这里我们尝试再加一个状态表示:
f[i]:以i位置为结尾,i位置为“上升”的最大湍流子数组的长度
g[i]:以i位置为结尾,i位置为“下降”的最大湍流子数组的长度
2.状态转移方程
dp[i]等于什么?
以i位置为结尾有三种情况:
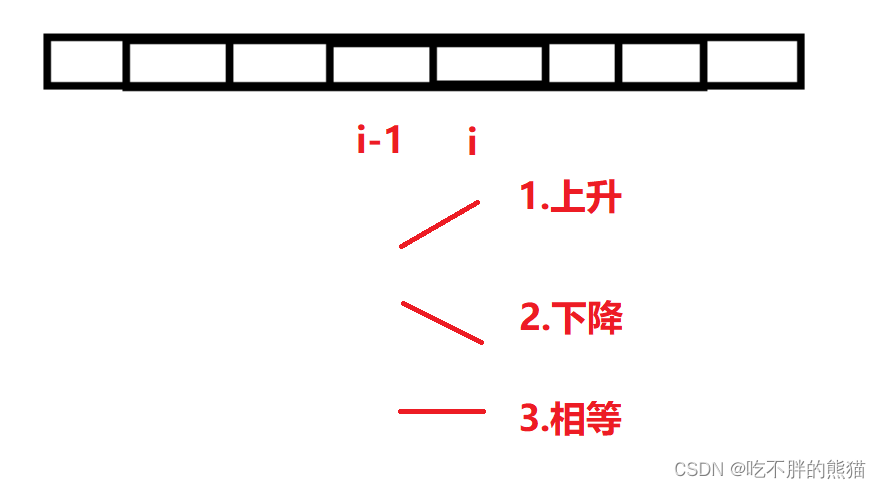
只有是情况1和2时才有可能时湍流子数组;
根据我们的状态表示:
情况一(i位置为“上升”):
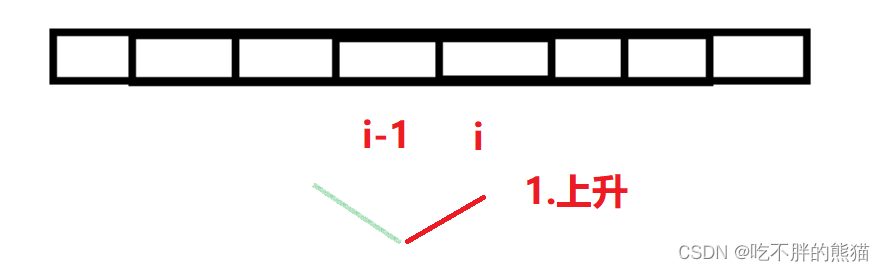
那么需要前面一个位置是“下降”的才满足湍流子数组;
所以此时i位置的最长湍流子数组应该是前面一个位置为“下降”的最长湍流子数组的长度+1;
而“前面一个位置为“下降”的最长湍流子数组的长度”就是我们的状态表示:g[i-1]
所以:f[i]=g[i-1]+1
情况二(i位置为“下降”):
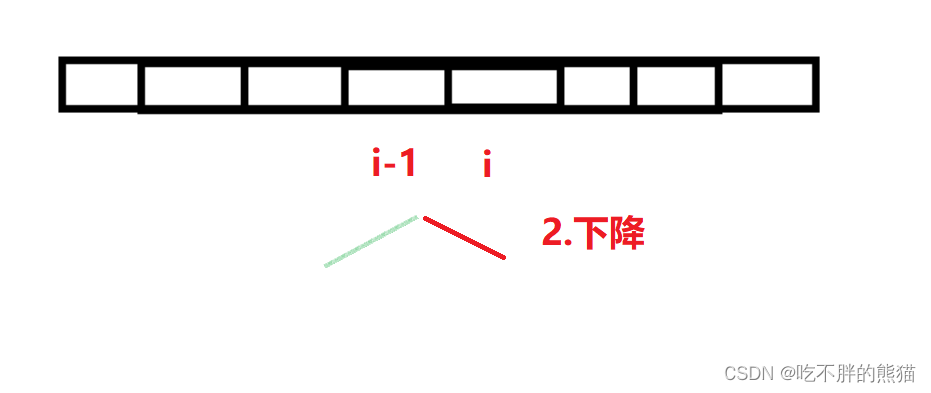
那么需要前面一个位置是“上升”的才满足湍流子数组;
所以此时i位置的最长湍流子数组应该是前面一个位置为“上升”的最长湍流子数组的长度+1;
而“前面一个位置为“上升”的最长湍流子数组的长度”就是我们的状态表示:g[i-1]
所以:g[i]=f[i-1]+1
3.初始化
(保证填表的时候不越界)
我们是从第二个元素比的,所以把要把前面的都初始化为1
4.填表顺序
(为了填写当前状态的时候,所需要的状态已经计算过了)
这里所需要的状态是:[i-1]
所以填表顺序从左往右
5.返回值
(根据题目要求和状态表示)
综上分析:
返回值为:两个表里的最大值
编写代码:

class Solution {
public:int maxTurbulenceSize(vector<int>& arr) {//1.创建dp表//2.初始化//3.填表//4.返回结果int n=arr.size();vector<int> f(n+1,1);auto g=f;int ret=1;for(int i=2;i<n+1;i++){if(arr[i-1]>arr[i-2]){f[i]=g[i-1]+1;}else if(arr[i-1]<arr[i-2]){g[i]=f[i-1]+1;}ret=max({(int)ret,g[i],f[i]});}return ret;}
};这篇关于【动态规划】24子数组系列_最长湍流子数组_C++的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!


