本文主要是介绍图解 | 你管这破玩意叫动态规划,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!

01
小宇:闪客,我最近在研究动态规划,但感觉就是想不明白,你能不能给我讲讲呀?
闪客:没问题,这个我擅长,你先说说提到动态规划,你最先想到的是什么?
小宇:就什么子问题呀、状态转移方程呀乱七八糟的,哎呀不行不行,我一想到这些脑子又嗡嗡响了。
闪客:你先别急,你先把所有的名词都抛在脑后,听我讲。
小宇:好滴,你说吧。
闪客:小宇我问你,从 1 一直加到 100 等于多少?
1 + 2 + 3 + ... + 100 = ?
小宇:5050!
闪客:你这,怎么不按套路出牌呀,你应该说不知道。
小宇:人家高斯早就算出来了,我还装不知道,这也太假了吧。
全剧终...
02
闪客:好吧,那我再给你出一个题。
小宇:行,你说吧,这回我肯定说不知道。
闪客:一个楼梯有 10 级台阶,你从下往上走,每跨一步只能向上迈 1 级或者 2 级台阶,请问一共有多少种走法?
小宇:额,这我真不知道了,我想想哈。

小宇:不行了不行了,实在想不明白,想了后面的就忘了前面的。
闪客:你还是陷入了穷举的思想,你仔细想想我给你出的第一个题,看看有没有思路。
小宇:啊!原来是有关联的呀。
闪客:对呀,我本来想说假如我告诉你 1+...+99 是多少,你是不是就直接能算出 1+...+100 的值了。
小宇:哦你这么一提示我有点感觉了!要想走到第 10 级台阶,要么是先走到第 9 级,然后再迈一步 1 级台阶上去,要么是先走到第 8 级,然后一次迈 2 级台阶上去。

闪客:太棒了!你找到感觉了!接着往下说。
小宇:这样的话,走到 10 级台阶的走法数,就等于走到 9 级台阶的走法数,加上走到 8 级台阶的走法数。
闪客:很好,那假如走到第 x 级台阶的走法数我们定义为 F(x),那你能把刚刚的描述公式化么?
小宇:那太简单了,公式就是:
F(10) = F(9) + F(8)
闪客:没错,而且不光是 10 级台阶如此,走到任何一级台阶的走法数,都符合这个逻辑,因此就可以得出一个通用公式:
F(x) = F(x-1) + F(x-2)
小宇:嗯嗯,这样计算 F(10),只需要知道 F(9) 和 F(8) 就可以了,而计算 F(8),就只需要知道 F(7) 和 F(6) 就可以了,依次类推。
闪客:没错,那你想想看 F(2) 和 F(1) 怎么计算?
小宇:简单,还是刚刚都逻辑被,想知道 F(2),只需要知道 F(1) 和 F(0),诶不对 F(0) 是什么鬼?还有 F(1) 的计算需要知道 F(0) 和 F(-1),不行呀,这解释不通了。
闪客:哈哈,别急,在这道题里,如果只迈到 1 级台阶,那一共就一种走法;如果只迈到 2 级台阶,就只有两种走法。可以直接很直观地得出,没必要推导。
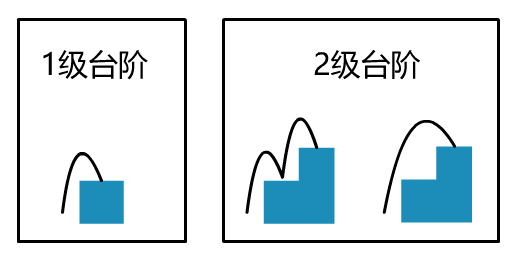
小宇:哦哦我懂了,这道题里由于每一个递推项都需要前两项的支持,所以必须有最开头的两项作为已知,就是你说的 F(1) = 1 和 F(2) = 2。
闪客:没错。
小宇:嗯嗯,感觉这样就推出全部结果了!我写一下程序你看看。
闪客:先别急,由于这道题是一道经典的动态规划题,所以我们以这道题为例子来定义动态规划的三要素,在本题中
F(x-1) 和 F(x-2) 被称为 F(x) 的最优子结构
F(x) = F(x-1) + F(x-2) 叫状态转移方程
F(1) = 1, F(2) = 2 是问题的边界
之后做动态规划问题,只要找好这三个要素就好了。
小宇:哇,升华了诶,逼格瞬间高了不少呢。
闪客:先别说这些废话了,那接下来你看看能不能写出程序,计算出 F(10) 的结果,这才是难点。
小宇:编程的话这似乎是个递归问题,简单!
int getWays(int n) {if (n == 1) {return 1;}if (n == 2) {return 2;}return getWays(n-1) + getWays(n-2);
}
闪客:嗯不错,这样很简洁,但复杂度太高了,是 O(2^n),具体你可以之后想想为什么。现在你看看能不能将复杂度降低。
小宇:我想想看,计算 F(10) 时需要计算 F(9) 和 F(8),而在递归计算 F(9) 时要计算 F(8) 和 F(7),这样 F(8) 在这里重复计算了,浪费了时间。
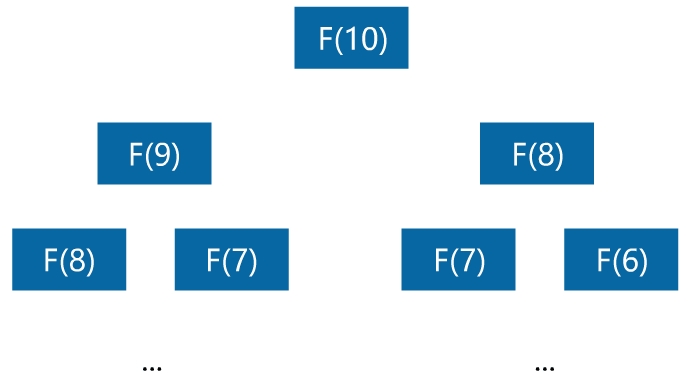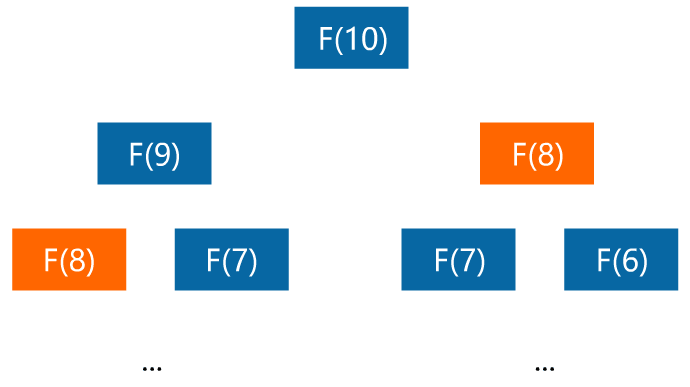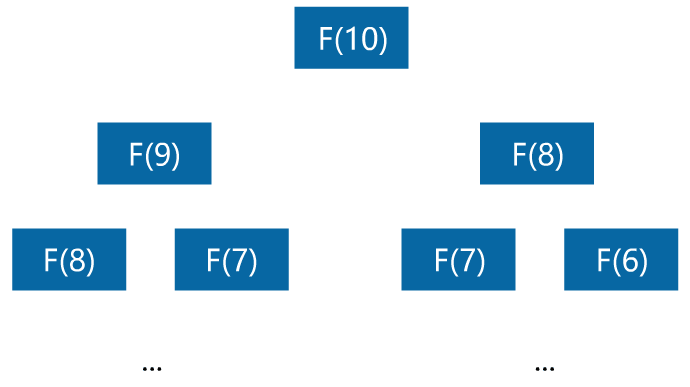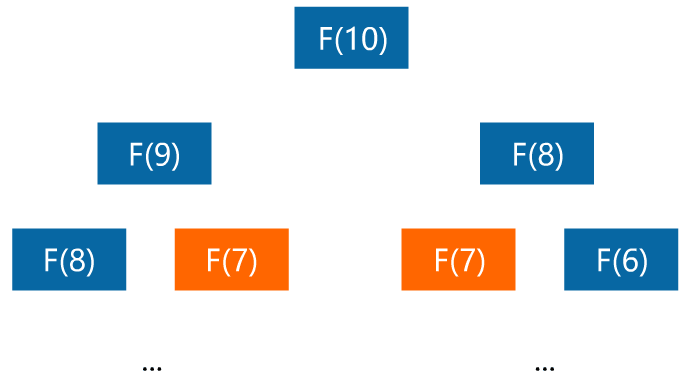
闪客:没错,其实计算新一个阶段的值,只需要一直将其前两个阶段的值保存起来,就可以一直算到最终的结果了。比如定义两个变量 a 和 b 用于存储前两个阶段的值,在计算 F(3) 时。
| 台阶 | 1 | 2 | 3 | 4 | ... | 10 |
| 走法 | a=1 | b=2 | 3 |
计算 F(4) 时,F(1) 的值就不用保存了,a 和 b 依次替换新值。
| 台阶 | 1 | 2 | 3 | 4 | ... | 10 |
| 走法 | a=2 | b=3 | 5 |
依此类推,最终就算出了 F(10) 的值。
| 台阶 | 1 | 2 | ... | 8 | 9 | 10 |
| 走法 | a=34 | b=55 | 89 |
当然你也可以把之前的值都保留,但这样就增加了空间复杂度,看你的需求了。
小宇:好的,那这样代码也很好写,就这样。
int getWays2(int n) {if (n == 1) {return 1;}if (n == 2) {return 2;}int a = 1;int b = 2;int temp = 0;for (int i = 3; i <= n; i++) {temp = a + b;a = b;b = temp;}return temp;
}
闪客:不错,这就是这道题正确的动态规划解法,而且时间复杂度是 O(N),空间复杂度是 O(1)
小宇:哇,这就是动态规划呀,原来这么简单。
03
闪客:不错,动态规划理解起来不难,难在当需要考虑的因素,也就是变化的维度多起来的时候,有的人就会头脑发蒙,不好找递推公式了,而且这也确实是个难点。
小宇:哦是吗?
闪客:那当然,我再给你出一道题。
小宇:来吧兄弟。
闪客:咳咳,那你听好了。
有一个背包,可以装载重量为 5kg 的物品。
有 4 个物品,他们的重量和价值如下。

那么请问,在不得超过背包的承重的情况下,将哪些物品放入背包,可以使得总价值最大?
小宇:明白了,就是我用这个背包最多能装走多少钱的东西。
闪客:是的。
小宇:哎呀不行,我又陷入走楼梯时的遍历思想了。
闪客:没关系,这道题能想出遍历思想,其实也不容易了,你可以先说一下,找找感觉。
小宇:嗯嗯,那就是每个物品都可以有放入背包和不放入背包两种选择。
如果总重量超过了背包承重,那就不算,或者说将价值记为 0,然后将所有情况中价值最大的那个作为结果。
这样的复杂度也很容易得出,就是 O(2^N)
闪客:没错,这个复杂度很高的算法你已经说的很明白了,那接下来你想想看用动态规划思想,能不能解决这个问题。
小宇:好的,你之前说过,动态规划的三要素是最优子结构、状态转移方程和边界
闪客:没错,之前的变量很少所以比较简单,现在变量多了,定义就变得难了起来,我们先来几个定义方便描述。我们将 4 个物品的重量和价值分别表示为:w1,w2,w3,w4,v1,v2,v3,v4。

假如我们用
F(W,i)
表示
用载重为 W 的背包,装前 i 件物品的最大价值
那本题其实就是
用载重为 5kg 的背包,装前 4 件物品的最大价值
其实就是求解
F(5,4)
你能找到状态转移方程么?
小宇:我想想,单看这个物品 4,有两种可能:
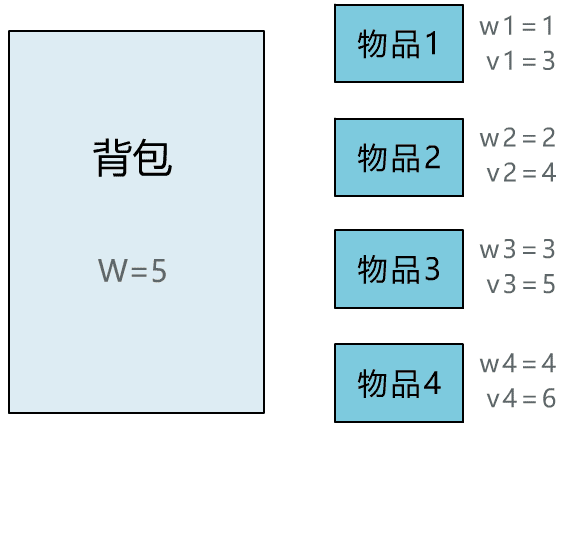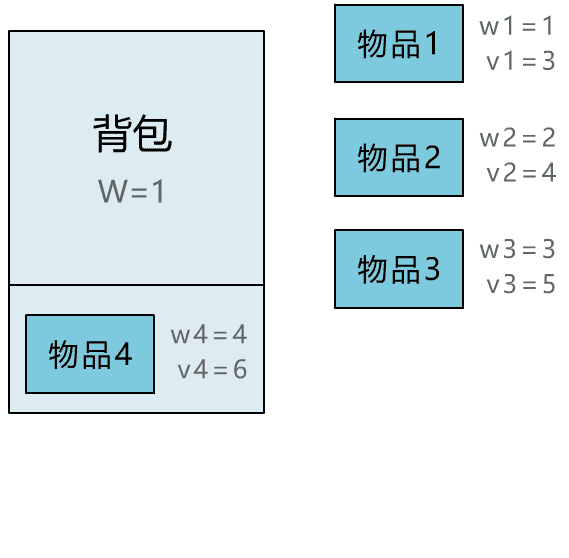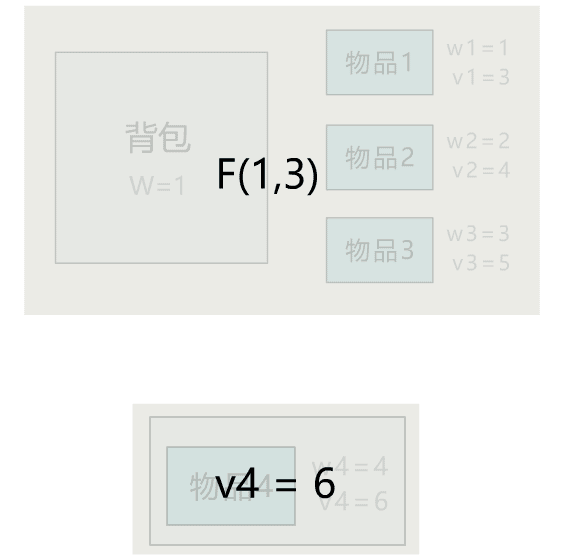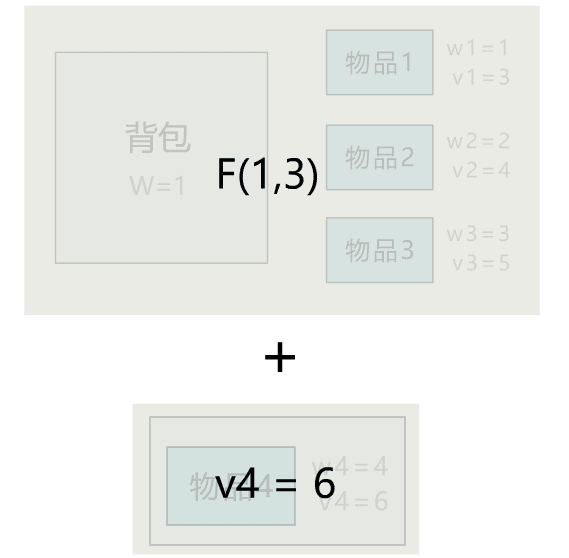
第一种可能:如果选择把它装入背包,那已经得到了 6 元钱。
此时背包剩余载重为 1kg(5kg-4kg),剩余物品是除去物品 4 后的前 3 件物品。
那这部分能获取到的最大价值,相当于
用一个载重为 1kg 的背包,装前 3 件物品的最大价值
哇,那这部分就是
F(1,3)
闪客:哈哈,你这自己说着说着就说对啦!
小宇:所以最终,如果选择将物品 4 放入背包,这种情况下,最大价值就等于二者之和。
F(1, 3) + 6
闪客:太好了小宇,那另一种情况呢?
小宇:第二种可能:如果选择不装这个物品 4,那更简单了,就直接等于用一个载重为 5 的背包装前 3 件物品的价值。
F(5, 3)

闪客:没错,而且就只有这两种情况!所以你看看 F(5,4)是否能用这两种情况的值表示呢?
小宇:哈哈,很简单,就等于这两种情况当中的最大值呗。
F(5,4) = max { F(1, 3) + 6,F(5, 3) }
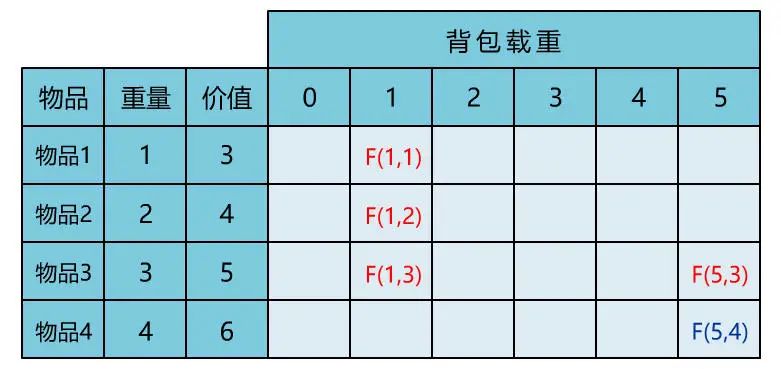
闪客:太好了,现在状态转移方程出来了,此时我们画个表格。

我们的目标就是要计算右下角那个值,即背包载重 W = 5 时,选择前 4 件物品放入背包的最大价值 F(5,4)
小宇:哇这个表格好清晰呀,根据上面的公式
F(5,4) = max { F(1,3) + 6, F(5,3) }
那也就是说只要知道 F(1,3) 和 F(5,3) 的值就可以了对吧?

闪客:没错,那你再看看 F(1,3) 怎么计算?
小宇:好的,F(1,3) 此时背包重量为 1,如果选择放第三件物品的话,诶?好像不行,第三件物品根本放不下呀!
闪客:是的,所以这种情况就没必要讨论放第三件物品的情况了,因为根本放不下,因此 F(1,3) 直接就等于 F(1,2),所以只需要知道 F(1,2) 即可。

同理 F(1,2) 也直接等于 F(1,1),因为在背包重量为 1 时第二件物品也放不下。
闪客:小宇你想想看,那 F(1,1) 又等于什么呢?
小宇:显然嘛,现在只有一件物品可以选了,那能放下当然就放咯,所以最大价值就是第一件物品的价值 3,即 F(1,1) = 3
闪客:没错,这样我们就找到了一个边界值,小宇你想想看还有哪些边界值可以直接得出?你写在表格里吧。
小宇:好的,首先第一列表示背包重量为 0 时的情况,那显然什么都装不了,就全都是 0 了。
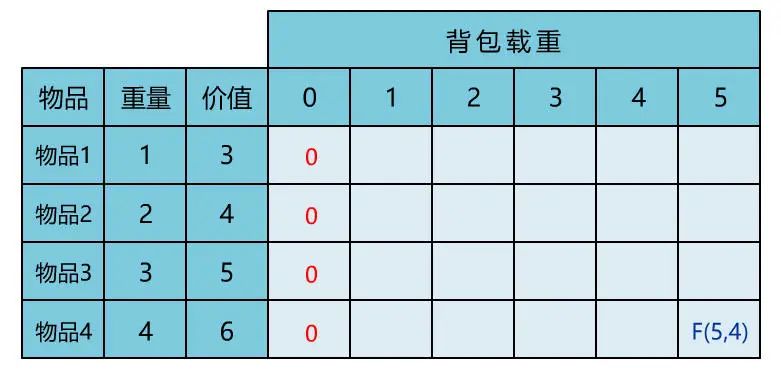
然后第一行也比较好算,背包重量 >= 1 时可以放下第一件物品,所以最大价值都等于 3
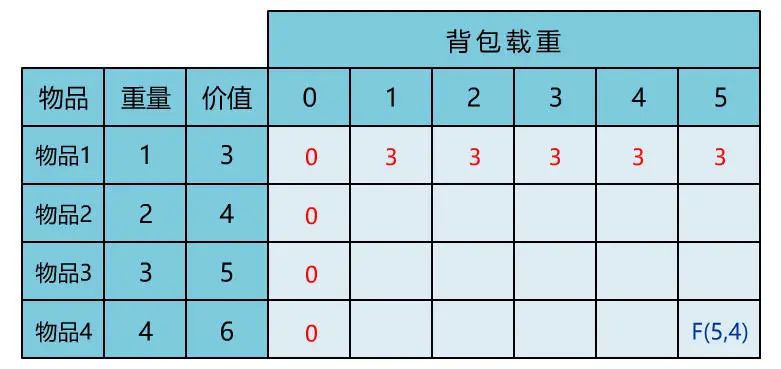
闪客:很好,接下来,就依次把表格的所有项都填出来,自然就可以算出 F(5,4) 啦。

小宇:哇塞,这样看好清晰呀!
闪客:是呀,不过刚刚我们用的都是具体的数字,那我们试着把这个问题抽象化,用一个载重为 W 的背包,装载 N 件物品,每件物品的重量和价值分别用 wi 和 vi 来表示,那刚刚的状态转移方程是什么呢?
小宇:emm,刚刚 F(5,4) = max { F(1,3) + 6, F(5,3) },如果都用变量表示的话,就是
F(W,N) =
max { F(W-wn, N-1) + vn,F(W, N-1) }
闪客:很好,这就是状态转移方程。
F(W-wn, N-1) 和 F(W, N-1) 就是 F(W,N) 的最优子结构。
而刚刚表格中的第一行和第一列,即 F(0,...) 和 F(...,1) 就是边界值!
小宇:哇塞我爱你闪客!终于有点理解动态规划的思想了呢!
04
闪客:别高兴太早,虽然过程看着清晰了,但代码写起来还是有难度的,你今天回去就把代码试着实现一下吧。
小宇:好的,保证完成任务。
闪客:快到晚饭时间了,旁边新开了家饺子馆,要不要一块去吃呀?
小宇:哦不了,晚上想利用晚饭时间再去消化消化动态规划的知识,不是还得代码实现呢么,下次吧,
闪客:哦好吧~


我知道你在看哟

这篇关于图解 | 你管这破玩意叫动态规划的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







