【精品课设】经典PID与专家PID控制的对比与分析（二）

【精品课设】经典PID与专家PID控制的对比与分析（二）

写在前面-研究背景：

 1.本代码基于MATLAB2019a版本，低版本或者不同版本可能会报错，mdl文件或slx文件打开可能会失败；
 2.如果运行时间过长，请观察设置参数是否一致。
 3.本博客附上算法运行图并详细介绍，如果转载请注明出处；
 4.如果本博客恰巧与您的研究有所关联，欢迎您的咨询qq1366196286 。

1经典PID控制的设计与仿真

   经典PID控制的设计与仿真可参照上一篇博客，【精品课设】经典PID与模糊PID控制的对比与分析（一）

1.1 被控对象传递函数的设计

   被控对象的传递函数为：

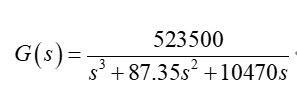
1.2 经典PID控制的仿真

Traditional_PID.m

clc,
close all;
clear all; %#ok<CLALL>
warning off;rin = 1.0; % 设定系统的参考输入量-单位阶跃响应
ts=0.001; %设置系统采样的时间--运行时间1.0ssys=tf(5.235e005,[1, 87.35, 1.047e004, 0]); %设置被控对象的传递函数dsys=c2d(sys,ts,'tustin');    %离散化处理-Z域
[num,den]=tfdata(dsys,'v');u_1=0.0;u_2=0.0;u_3=0.0; % 系统初始值的0初始化
y_1=0;y_2=0;y_3=0;x=[0,0,0]';  %中间变量的初始化
e_1=0; %对误差的初始化
ec_1=0;%% 未进行整定
kp0=0.90; % PID控制参数的大小
ki0=0.05;
kd0=0.2;% 对系统进行建模
for k=1:1:1000time(k)=k*ts;
% r(k)=sign(sin(2*pi*k*ts)); %%脉冲输入
r(k)=rin; %%单位阶跃输入u(k)=kp0*x(1)+ki0*x(2)+kd0*x(3);% if k==300     % Adding disturbance(1.0v at time 0.3s)施加干扰量
%    u(k)=u(k)+1.0;
% endy(k)=-den(2)*y_1-den(3)*y_2-den(4)*y_3+num(1)*u(k)+num(2)*u_1+num(3)*u_2+num(4)*u_3;
e(k)=r(k)-y(k);
%%%%%%%%%%%%%%Return of PID parameters%%%%%%%%%%%%%%%u_3=u_2;u_2=u_1;u_1=u(k);y_3=y_2;y_2=y_1;y_1=y(k);x(1)=e(k);            % Calculating Px(2)=e(k)-e_1;        % Calculating Dx(3)=x(3)+e(k)*ts;    % Calculating Iec_1=x(2);e_2=e_1;e_1=e(k);
end
%% 绘制响应输出
clf,
figure(1);
plot(time,r,'b',time,y,'r');
xlabel('time(s)');ylabel('rin,yout');

程序运行结果图如下：

2专家PID控制的设计

2.1 专家PID控制律的设计

   专家系统主要由知识库和推理机构成，专家系统的结构如图1所示。

图1 专家系统的结构图

   专家PID控制实质是：基于受控对象和控制规律的各种知识，无须知道被控对象的精确模型，利用专家经验来设计PID参数。专家PID控制是一种直接型专家控制器。其中，直接型专家控制器，如图2所示。

图2 直接型专家控制器的结构图

   具体实现过程可参照《智能控制》书中P12-P13页。

2.2 专家PID控制的仿真结果

图3 PID控制阶跃响应的输出曲线

图4 误差响应曲线

3仿真对比与分析

  将专家PID控制与传统PID控制的输出响应进行对比，可得：

  将专家PID控制、模糊PID控制与传统PID控制的输出响应进行对比，可得：