本文主要是介绍Chapter 3:有限Markov决策过程,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
Chapter 3:Finite Markov Decision Processes
- 2.1 Agent–Environment交互
- Markov transition graph
- 3.2 Goals and Rewards
- 3.2.1 returns and episodes
- 3.2.2 episodic tasks和continuing tasks的统一表示
- 3.3 Policy and Value function
- 3.4 Optimal Policies and Optimal Value Functions
- 3.5 Optimality and Approximation
有限MDPs问题和老虎机问题一样,也是评价性反馈,但是和bandit问题不同的是,MDPs问题除了immediate reward还涉及到delayed reward,需要在直接奖励和延迟奖励之间权衡。
在bandit问题中,估计的是每个动作 a a a的value q ∗ ( a ) q_*(a) q∗(a);在MDPs中,估计的是每个状态 s s s下的每个动作 a a a的value q ∗ ( s , a ) q_*(s,a) q∗(s,a),或者估计给定最佳动作选择后每个状态的value v ∗ ( s ) v_*(s) v∗(s)。
本章介绍了MDPs问题的数学结构的关键元素:如returns,value function,Bellman equation。函数和Bellman方程。与所有人工智能一样,该问题在适用范围和数学易处理性之间存在着一种权衡。
2.1 Agent–Environment交互

事件发生顺序:

在有限MDPs中,状态、动作和奖励 ( S , A , R ) (\mathcal{S,A,R} ) (S,A,R)集合都具有有限数量的元素。因此,随机变量 R t R_t Rt和 S t S_t St具有明确定义的离散概率分布,仅取决于先前的状态和动作。
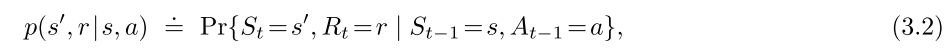
函数 p : S × R × S × A → [ 0 , 1 ] p:\mathcal{S\times R\times S\times A} \rightarrow[0,1] p:S×R×S×A→[0,1]是含有四个参数的普通确定性函数。函数 p p p表征了MDPs的动态。
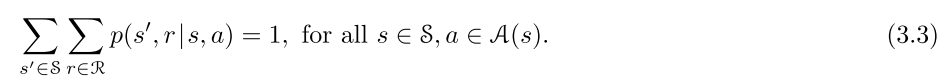
Markov property: 状态 s s s必须包含有关过去的agent-environment互动的所有信息。本书假设该性质成立。
根据带有4个参数的函数 p p p,可以推导出其他有关environment的函数:
state-transition probabilities:
含有3个参数的函数 p : S × S × A → [ 0 , 1 ] p:\mathcal{S\times S\times A} \rightarrow[0,1] p:S×S×A→[0,1]
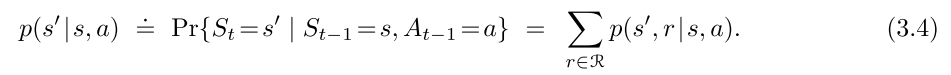
expected rewards for state–action pairs:
含有2个参数的函数 p : S × A → R p:\mathcal{S\times A} \rightarrow \mathbb R p:S×A→R)
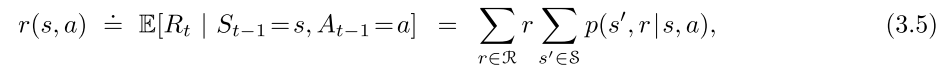
expected rewards for state–action-next state triples:
含有3个参数的函数 p : S × A × S → R p:\mathcal{S\times A \times S} \rightarrow \mathbb R p:S×A×S→R)
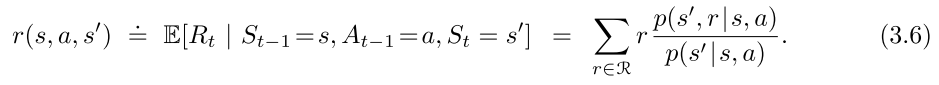
Markov transition graph

图种有两种节点:state nodes和action nodes
3.2 Goals and Rewards
如果采取的动作不仅有直接奖励,还有延迟奖励,那么目标变为最大化该行动带来的奖励(reward)累积和的期望价值(expected value)。
理解:最大化收到的reward总和(in the long run)。
3.2.1 returns and episodes
return G t G_t Gt:step t t t之后的收到的rewards之和
G t = R t + 1 + R t + 2 + . . . + R T ( 3.7 ) G_t=R_{t+1}+R_{t+2}+...+R_T(3.7) Gt=Rt+1+Rt+2+...+RT(3.7)
episodes:
当agent-environment交互能自然地分解为子序列时,把子序列叫作episodes,有些文献中也叫trials。
terminal state: 每个episode每集的结束状态。所有episodes都可以被认为是以相同的终端状态结束,但是对不同的结果有不同的奖励。
episodic tasks: 包括多个episodes的tasks。 S \mathcal S S表示非终结状态的集合, S + \mathcal S^+ S+表示非终结状态加终结状态的集合。终止时间 T T T是随机变量,根据不同的episode 变化。
continuing tasks: 不能被分解成episodes的tasks,实际情况中很多都是连续任务,此时式(3.7)不再适用,因为 T = ∞ T=\infin T=∞。
所以我们用了一个稍微复杂一点的return定义,引入了discounting,便于计算。
折现
选择 A t A_t At最大化expected discounted return:
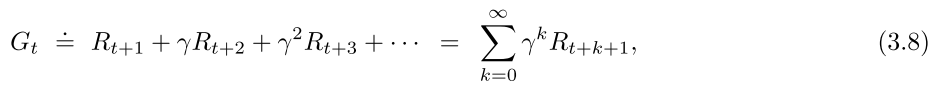
γ ∈ [ 0 , 1 ] \gamma\in [0,1] γ∈[0,1]:折现率
γ < 1 \gamma<1 γ<1:如果 R k R_k Rk有限,式(3.8)是有限。
γ = 0 \gamma=0 γ=0:myopic,只考虑了直接奖励。
γ \gamma γ越接近1,说明越有远见,考虑future reward越多。
递推关系:
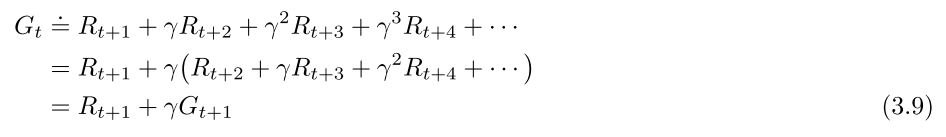
3.2.2 episodic tasks和continuing tasks的统一表示
对于episodic tasks来说,虽然又很多个episodes,但是我们通常只考虑其中单个的episode。
所以可以统一表示为:

其中,KaTeX parse error: Expected 'EOF', got '\infine' at position 3: T=\̲i̲n̲f̲i̲n̲e̲表示continuing tasks; γ = 1 \gamma=1 γ=1表示episodic tasks。两个条件不能同时满足。
3.3 Policy and Value function
policy: 从状态到选择每个可能动作的概率的映射。 例如:现在有policy π \pi π,则 π ( a ∣ s ) \pi(a|s) π(a∣s)表示 S t = s S_t=s St=s时 A t = a A_t=a At=a的概率。
value function: 在policy π \pi π 和state s s s 下的expected return记作 v π ( s ) v_\pi(s) vπ(s)
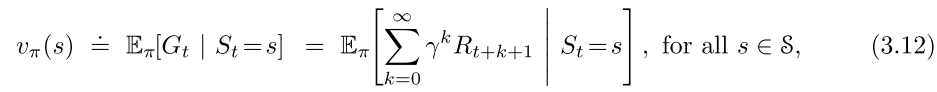
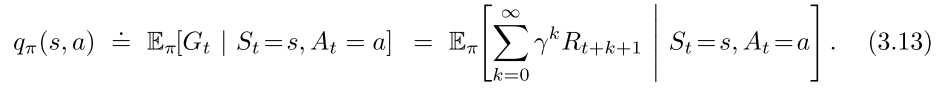
v π v_\pi vπ是policy π \pi π 的state-value function; q π q_\pi qπ是policy π \pi π 的action-value function。
Bellman equation: 在policy π \pi π 和state s s s 下的expected return记作 v π ( s ) v_\pi(s) vπ(s)

式(3.14)是 v π v_\pi vπ的Bellman Equation,表示一个state价值与其下一阶段的state价值之间的关系。
3.4 Optimal Policies and Optimal Value Functions
optimal state-value function:

optimal action-value function:

对于state-action pair s , a s,a s,a,函数 q ∗ ( s , a ) q_*(s,a) q∗(s,a)表示在状态 s s s中执行动作 a a a并且此后遵循最优策略 π \pi π的expected return。因此, q ∗ q_* q∗可以用 v ∗ v_* v∗表示:
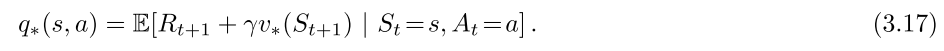
Bellman optimality equation:
含义:最优policy下的state value必须等于该state下的最佳action的expected return。

Bellman optimality equation for v ∗ v_* v∗:式(3.18)与式(3.19)
Bellman optimality equation for q ∗ q_* q∗:式(3.20)
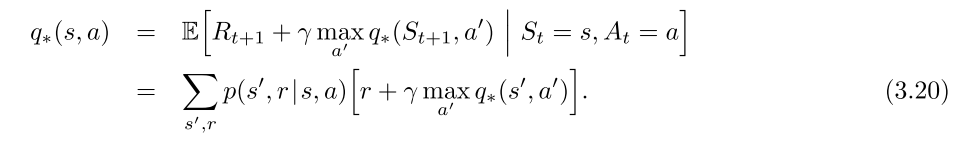
3.5 Optimality and Approximation
因为很多原因,现实中可能无法得到最优解policy,此时就需要近似。强化学习的Online性质使得有可能以更多的方式接近最优策略,以便为频繁出现的state做出正确的决策,而不用考虑到出现频率低的state。这是将强化学习与其他近似解决MDP的方法区分开来的一个关键属性。
这篇关于Chapter 3:有限Markov决策过程的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







