【数据结构与算法】之数组系列-20240116

本文主要是介绍【数据结构与算法】之数组系列-20240116，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

在这里插入图片描述

这里写目录标题

一、15. 三数之和
二、16. 最接近的三数之和
三、49. 字母异位词分组
四、53. 最大子数组和
五、189. 轮转数组
六、179. 最大数

一、15. 三数之和

提示
中等
给你一个整数数组 nums ，判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ，同时还满足 nums[i] + nums[j] + nums[k] == 0 。请
你返回所有和为 0 且不重复的三元组。
注意：答案中不可以包含重复的三元组。

示例 1：

输入：nums = [-1,0,1,2,-1,-4]
输出：[[-1,-1,2],[-1,0,1]]
解释：
nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0 。
nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0 。
nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0 。
不同的三元组是 [-1,0,1] 和 [-1,-1,2] 。
注意，输出的顺序和三元组的顺序并不重要。
示例 2：

输入：nums = [0,1,1]
输出：[]
解释：唯一可能的三元组和不为 0 。
示例 3：

输入：nums = [0,0,0]
输出：[[0,0,0]]
解释：唯一可能的三元组和为 0 。

class Solution:def threeSum(self,nums):res=[]nums.sort()n=len(nums)if n<3:return []for i in range(n):if nums[i]>0:return resL=i+1R=n-1while L<R:if nums[i]+nums[L]+nums[R]==0:res.append([nums[i],nums[L],nums[R]])while L<R and nums[L]==nums[L+1]:L=L+1while L<R and nums[R]==nums[R-1]:R=R-1L=L+1R=R-1elif nums[i]+nums[L]+nums[R]>0:R=R-1else:L=L+1return resnums = [-1, 0, 1, 2, -1, -4]
res = Solution()
rrr = res.threeSum(nums)
print(rrr)

二、16. 最接近的三数之和

中等

给你一个长度为 n 的整数数组 nums 和一个目标值 target。请你从 nums 中选出三个整数，使它们的和与 target 最接近。
返回这三个数的和。
假定每组输入只存在恰好一个解。

示例 1：
输入：nums = [-1,2,1,-4], target = 1
输出：2
解释：与 target 最接近的和是 2 (-1 + 2 + 1 = 2) 。

示例 2：
输入：nums = [0,0,0], target = 1
输出：0

思路：排序+双指针
我们将数组排序，然后遍历数组，对于每个元素nums[i],我们使用指针j和k分别指向i+1和n-1
计算三数之和，如果三数和等于target，则直接返回target，否则根据与target的差值更新答案
如果三数之和大于target，则将R向左移动一位，否则将L向右移动一位。

class Solution:def threeSumClosest(self,nums,target):ans=infnums.sort()n=len(nums)if n<3:return []for i in range(n):L=i+1R=n-1while L<R:if nums[i]+nums[L]+nums[R]==target:return targett=nums[i]+nums[L]+nums[R]if abs(t-target)<abs(ans-target):ans=tif t>target:R=R-1else:L=L+1return anss = Solution()
nums = [-1, 2, 1, -4]
target = 1
print(s.threeSumClosest(nums, target))

特别注意：
from math import inf是从math库中导入inf常量。
inf表示正无穷大的数值。它可以用于比较和计算中的特殊情况。
以下是一个示例代码，演示了如何使用inf常量：

from math import inf# 比较inf常量
print(inf > 100)  # 输出：True
print(inf < 1000)  # 输出：False# 计算inf常量
print(inf + 10)  # 输出：inf
print(inf * 2)  # 输出：inf
print(inf / 3)  # 输出：inf

在上面的示例中，我们可以看到inf常量与其他数值进行比较时，inf常量始终被认为是最大的数值。
在计算中，任何数值与inf常量相加、相乘或相除，结果都将是inf常量。

三、49. 字母异位词分组

中等
给你一个字符串数组，请你将字母异位词组合在一起。可以按任意顺序返回结果列表。
字母异位词是由重新排列源单词的所有字母得到的一个新单词。

示例 1:
输入: strs = [“eat”, “tea”, “tan”, “ate”, “nat”, “bat”]
输出: [[“bat”],[“nat”,“tan”],[“ate”,“eat”,“tea”]]
示例 2:
输入: strs = [“”]
输出: [[“”]]
示例 3:
输入: strs = [“a”]
输出: [[“a”]]

class Solution:def func(self,strs):d=defaultdict(list)for item in strs:key=''.join(sorted(item))d[key].append(item)return list(d.values())ss=Solution()
strs = ["eat", "tea", "tan", "ate", "nat", "bat"]
print(ss.func(strs))

四、53. 最大子数组和

中等
给你一个整数数组 nums ，请你找出一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。
子数组是数组中的一个连续部分。

示例 1：
输入：nums = [-2,1,-3,4,-1,2,1,-5,4]
输出：6
解释：连续子数组 [4,-1,2,1] 的和最大，为 6 。

示例 2：
输入：nums = [1]
输出：1

示例 3：
输入：nums = [5,4,-1,7,8]
输出：23

class Solution:def lianxu(self, nums):pre = 0max_sum = nums[0]i = 0while i < len(nums):if pre < 0:pre = 0pre = pre + nums[i]     # -2     1if max_sum < pre:       # -2<0   -2<1max_sum = pre       # 0      1i += 1                  # 1      2return max_sumnums = [5, 4, -1, 7, 8]ss = Solution()
print(ss.lianxu(nums))

五、189. 轮转数组

中等
给定一个整数数组 nums，将数组中的元素向右轮转 k 个位置，其中 k 是非负数。

示例 1:
输入: nums = [1,2,3,4,5,6,7], k = 3
输出: [5,6,7,1,2,3,4]
解释:
向右轮转 1 步: [7,1,2,3,4,5,6]
向右轮转 2 步: [6,7,1,2,3,4,5]
向右轮转 3 步: [5,6,7,1,2,3,4]

示例 2:
输入：nums = [-1,-100,3,99], k = 2
输出：[3,99,-1,-100]
解释:
向右轮转 1 步: [99,-1,-100,3]
向右轮转 2 步: [3,99,-1,-100]

思路：
先整体反转数组，即反转[0,n-1]区间
然后分别反转[0,k-1]和[k,n-1]区间即为结果

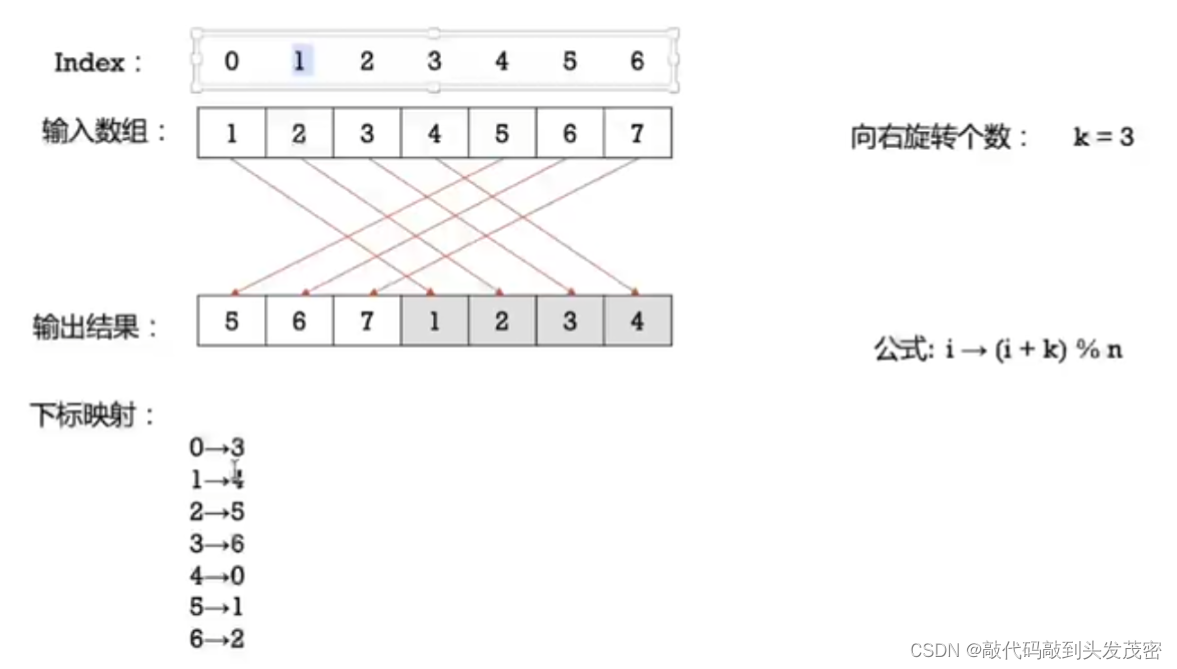
在这里插入图片描述
具体举例如下：

例如将4-5-6-7-8向右轮转3个位置。即k=3。首先整体翻转
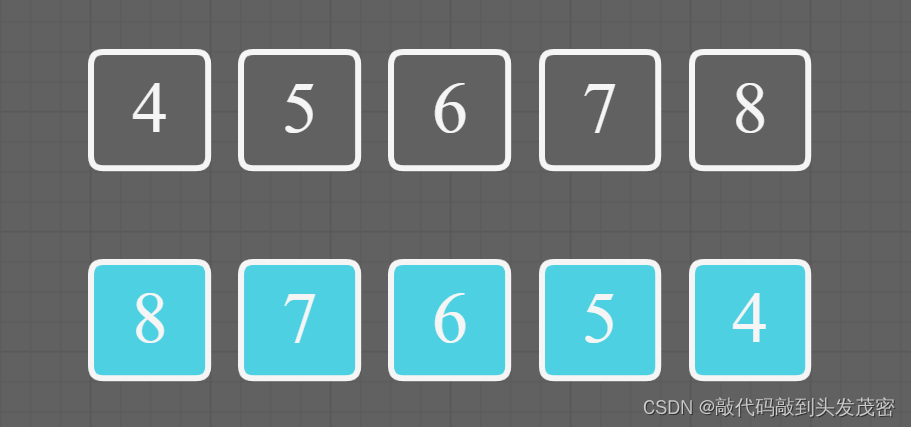
在这里插入图片描述
然后分别翻转[0,k−1]和[k,n−1]（先后无所谓）
如下翻转8-7-6

再翻转5-4，得到最后的结果

class Solution:def retate(self,nums,k):k=k%len(nums)       #映射后的下标的位置self.reverse(nums,0,len(nums)-1)self.reverse(nums,0,k-1)self.reverse(nums,k,len(nums)-1)return numsdef reverse(self,nums,start,end):while start<end:nums[start],nums[end]=nums[end],nums[start]start+=1end-=1ss=Solution()
nums = [1,2,3,4,5,6,7]
k = 3
print(ss.retate(nums, k))

六、179. 最大数

中等
相关标签
相关企业
给定一组非负整数 nums，重新排列每个数的顺序（每个数不可拆分）使之组成一个最大的整数。

注意：输出结果可能非常大，所以你需要返回一个字符串而不是整数。

示例 1：

输入：nums = [10,2]
输出：“210”
示例 2：

输入：nums = [3,30,34,5,9]
输出：“9534330”

思路：1、先将列表的数字通过map函数映射为字符串，再转化为列表
2、将列表中的字符，通过sorted方法按照降序排序
3、遍历字符串，如果相邻两个字符的首字符相同，判断当前字符的末尾与下一个字符的首位进行比较，如果当前字符的末位小于下一个字符的首位，则进行交换位置

def fn(nums):#todo 1先根据首位排序s = list(map(str, nums))    #利用map映射函数print(s)            #['3', '30', '34', '5', '9']ordered = sorted(s, key=lambda x: x, reverse=True)  #通过sorted降序排序print(ordered)      #['9', '5', '34', '30', '3']#todo 2、首位相同的，进行二次排序for i in range(len(ordered) - 1):#todo 如果相邻两个字符的首字符相同，if ordered[i][0] == ordered[i + 1][0]:# todo 判断当前字符的末尾与下一个字符的首位进行比较，#todo  如果当前字符的末位小于下一个字符的首位，则进行交换位置if int(ordered[i][-1]) < int(ordered[i + 1][0]):ordered[i], ordered[i + 1] = ordered[i + 1], ordered[i]return ''.join(ordered)
nums = [10,2]
res=fn(nums)
print(res)