本文主要是介绍C#,求最长回文字符串的马拉车(Manacher)算法的源代码,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
一、回文字符串(Palindromic String)
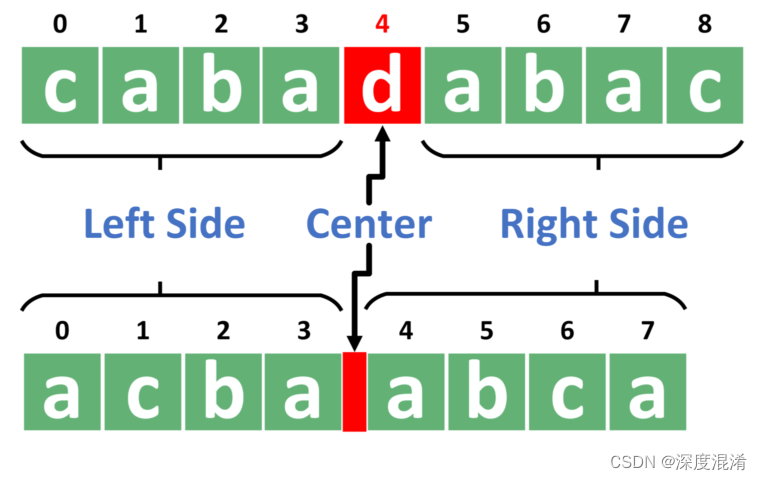
回文字符串(Palindromic String)是指前、后向读起来完全相同的字符串。
回文字符串除了答题似乎没有什么用处 :P
二、求解思路
求解字符串的回文子串的基本思路:
1、遍历每个位置;
2、先看有没有以位置i为中心的回文串(举例ABCBA)。所以我们要比较i+1和i-1是否相等,i+2和i-2是否相等,一直比较到字符串某一端点结束,或者中途发现不等的字符;
3、再看有没有以位置i为对称中心的回文串(举例ABBA)。所以我们要先看i和i+1等不等,如果等,那再看i-1和i+2是否相等,i-2和i+3是否相等,一直比较到字符串某一端点结束,或者中途发现不等的字符。
Manacher算法是一位名叫Manacher的人在1975年提出的一种算法,解决的问题是求最长回文子串。Manacher算法的核心思路就是利用之前求得的臂长( 即之前求出的Len值) 来减少时间复杂度,也就是说通过前面求出的Len值来加速求出当前下标i的 Len[i],快速求出所有的Len 值就是该算法的目的。
速度!
三、源代码
3.1 文本格式
using System;
using System.Text;
using System.Collections;
using System.Collections.Generic;
namespace Legalsoft.Truffer.Algorithm
{
// C# program to implement Manacher's Algorithm
// This code is contributed by PrinciRaj1992
public static class Palindromic_String
{
public static string Manacher(string text)
{
int N = text.Length;
if (N == 0)
{
return "";
}
N = 2 * N + 1;
int[] lengthArray = new int[N + 1];
lengthArray[0] = 0;
lengthArray[1] = 1;
int centerPosition = 1;
int centerRightPosition = 2;
int currentRightPosition = 0;
int currentLeftPosition;
int maxLPSLength = 0;
int maxLPSCenterPosition = 0;
int start = -1;
int end = -1;
int diff = -1;
// Uncomment it to print LPS Length array
for (currentRightPosition = 2; currentRightPosition < N; currentRightPosition++)
{
// get currentLeftPosition iMirror for currentRightPosition i
currentLeftPosition = 2 * centerPosition - currentRightPosition;
lengthArray[currentRightPosition] = 0;
diff = centerRightPosition - currentRightPosition;
// 如果 currentRightPosition 范围内
if (diff > 0)
{
lengthArray[currentRightPosition] = Math.Min(lengthArray[currentLeftPosition], diff);
}
// 尝试扩展以 currentRightPosition i为中心的回文。
// 对于奇数位置,我们比较字符,如果匹配,则将LPS长度增加1。
// 即使是位置,我们只是将LPS增加1,而不进行任何字符比较。
while (((currentRightPosition + lengthArray[currentRightPosition]) + 1 < N && (currentRightPosition - lengthArray[currentRightPosition]) > 0) &&
(((currentRightPosition + lengthArray[currentRightPosition] + 1) % 2 == 0) ||
(text[(currentRightPosition + lengthArray[currentRightPosition] + 1) / 2] == text[(currentRightPosition - lengthArray[currentRightPosition] - 1) / 2])))
{
lengthArray[currentRightPosition]++;
}
// 重新计算maxLPSLength
if (lengthArray[currentRightPosition] > maxLPSLength)
{
maxLPSLength = lengthArray[currentRightPosition];
maxLPSCenterPosition = currentRightPosition;
}
// 如果以currentRightPosition为中心的回文扩展到centerRightPosition之外,
// 根据扩展的回文调整centerPosition
if (currentRightPosition + lengthArray[currentRightPosition] > centerRightPosition)
{
centerPosition = currentRightPosition;
centerRightPosition = currentRightPosition + lengthArray[currentRightPosition];
}
}
start = (maxLPSCenterPosition - maxLPSLength) / 2;
end = start + maxLPSLength - 1;
if (end > start)
{
StringBuilder sb = new StringBuilder();
for (int i = start; i <= end; i++)
{
sb.Append(text.Substring(i, 1));
}
return sb.ToString();
}
return "";
}
}
}
-------------------------------------------------------
POWER BY TRUFFER.CN
3.2 代码格式
using System;
using System.Text;
using System.Collections;
using System.Collections.Generic;namespace Legalsoft.Truffer.Algorithm
{// C# program to implement Manacher's Algorithm// This code is contributed by PrinciRaj1992public static class Palindromic_String{public static string Manacher(string text){int N = text.Length;if (N == 0){return "";}N = 2 * N + 1;int[] lengthArray = new int[N + 1];lengthArray[0] = 0;lengthArray[1] = 1;int centerPosition = 1;int centerRightPosition = 2;int currentRightPosition = 0;int currentLeftPosition;int maxLPSLength = 0;int maxLPSCenterPosition = 0;int start = -1;int end = -1;int diff = -1;// Uncomment it to print LPS Length arrayfor (currentRightPosition = 2; currentRightPosition < N; currentRightPosition++){// get currentLeftPosition iMirror for currentRightPosition icurrentLeftPosition = 2 * centerPosition - currentRightPosition;lengthArray[currentRightPosition] = 0;diff = centerRightPosition - currentRightPosition;// 如果 currentRightPosition 范围内if (diff > 0){lengthArray[currentRightPosition] = Math.Min(lengthArray[currentLeftPosition], diff);}// 尝试扩展以 currentRightPosition i为中心的回文。// 对于奇数位置,我们比较字符,如果匹配,则将LPS长度增加1。// 即使是位置,我们只是将LPS增加1,而不进行任何字符比较。while (((currentRightPosition + lengthArray[currentRightPosition]) + 1 < N && (currentRightPosition - lengthArray[currentRightPosition]) > 0) &&(((currentRightPosition + lengthArray[currentRightPosition] + 1) % 2 == 0) || (text[(currentRightPosition + lengthArray[currentRightPosition] + 1) / 2] == text[(currentRightPosition - lengthArray[currentRightPosition] - 1) / 2]))){lengthArray[currentRightPosition]++;}// 重新计算maxLPSLengthif (lengthArray[currentRightPosition] > maxLPSLength){maxLPSLength = lengthArray[currentRightPosition];maxLPSCenterPosition = currentRightPosition;}// 如果以currentRightPosition为中心的回文扩展到centerRightPosition之外,// 根据扩展的回文调整centerPositionif (currentRightPosition + lengthArray[currentRightPosition] > centerRightPosition){centerPosition = currentRightPosition;centerRightPosition = currentRightPosition + lengthArray[currentRightPosition];}}start = (maxLPSCenterPosition - maxLPSLength) / 2;end = start + maxLPSLength - 1;if (end > start){StringBuilder sb = new StringBuilder();for (int i = start; i <= end; i++){sb.Append(text.Substring(i, 1));}return sb.ToString();}return "";}}
}这篇关于C#,求最长回文字符串的马拉车(Manacher)算法的源代码的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!



