重新学习数据结构和算法（持续更新）

前言

为什么写这篇文章：数据结构和算法是程序的灵魂，强烈建议大家认真学好这门学科，无论是对今后的工作生活、还是找工作亦或者是自己的思维都有巨大的帮助。相信我，一定要好好学，即将走入社会的我决定好好补一补大学期间没认真学的这门课。我是我重学《数据结构和算法》的学习笔记，java版本，在这里分享给大家，互帮互助共同进步。2021年4月23日开始编写，后期持续更新。
适宜人群：认同数据结构和算法很重要的同学（有一定数据结构基础）
你将学习到：常见的数据结构和算法
条件：一台可以运行“hello world”的电脑（暗示你们需要java环境）、一颗有毅力的心
资料参考：尚硅谷《Java数据结构和算法》、网络

注意：本文为笔者的学习笔记，仅供学习使用，本文部分图片来源于网路，如有侵权，请联系笔者删除。

第一章 先给大家打个气

如果你不想当码农，那就花时间来研究下数据结构和算法！
当你真心想要做一件事的时候，整个宇宙都会帮助你，加油！

第二章 初识数据结构和算法

1.线性结构和非线性结构

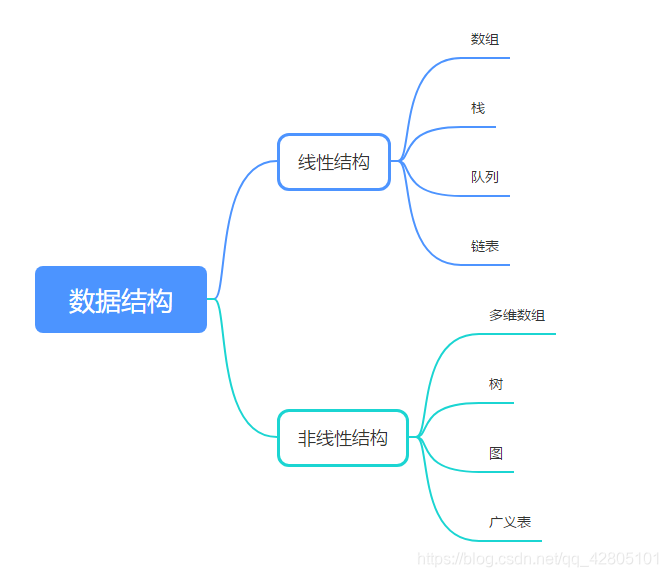
• 数据结构分为线性结构和非线性结构
• 线性结构又分为 顺序存储结构（数组） 和链式存储结构（链表）
• 顺序存储的链式表又叫做顺序表，顺序表中的存储元素是连续的

2.概览几种常见的数据结构

下面列举了几种常见的数据结构，先大概看一下它们长什么样子，帅不帅美不美，有没有你相中的。
2.1 数组
特点：查询快、增删慢
衍生物：一维数组、二维数组、多维数组、稀疏数组（下一章）等

2.2 链表
特点：查询慢、增删快
衍生物：单向链表、双向链表、循环链表（也分单双）

2.3 栈
特点：先进后出
衍生物：数组实现的栈、链表实现的栈

2.4 队列
特点：先进先出
衍生物：数组实现的队列、链表实现的队列

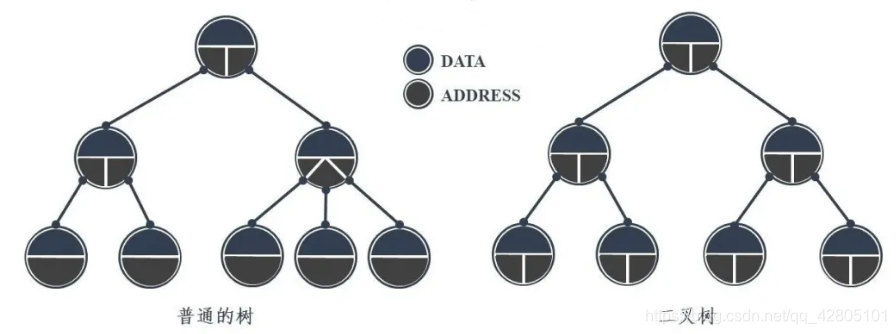
2.5 树
衍生物：二叉树、完全二叉树、满二叉树、二叉排序树、B+树、平衡二叉树、红黑树等（仿佛心里一点B树都没有，有点小怕）

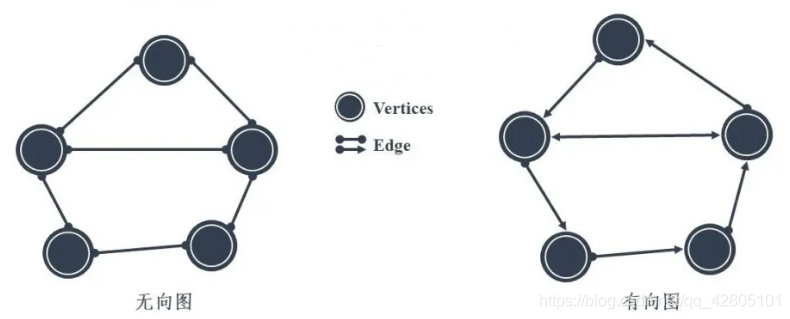
2.6 图

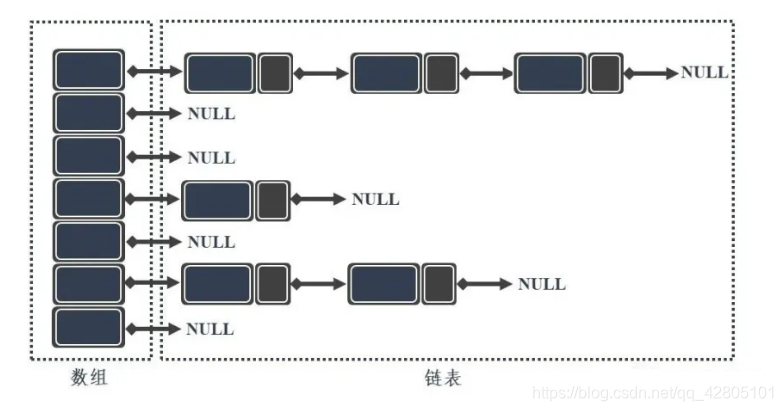
2.7 哈希表（散列表）
结构：数组+链表+红黑树（jdk1.8）

3.概览几种常见的算法思想

注意！！！这里看不懂没关系，直接跳（笔者编辑这里的时候也有很多不懂的，没事，慢慢来，等学完后面的章节后再回过头来看这里），现在你只需要浏览一两分钟就可以了，了解一下算法有哪些思想，混个耳熟
3.1 枚举

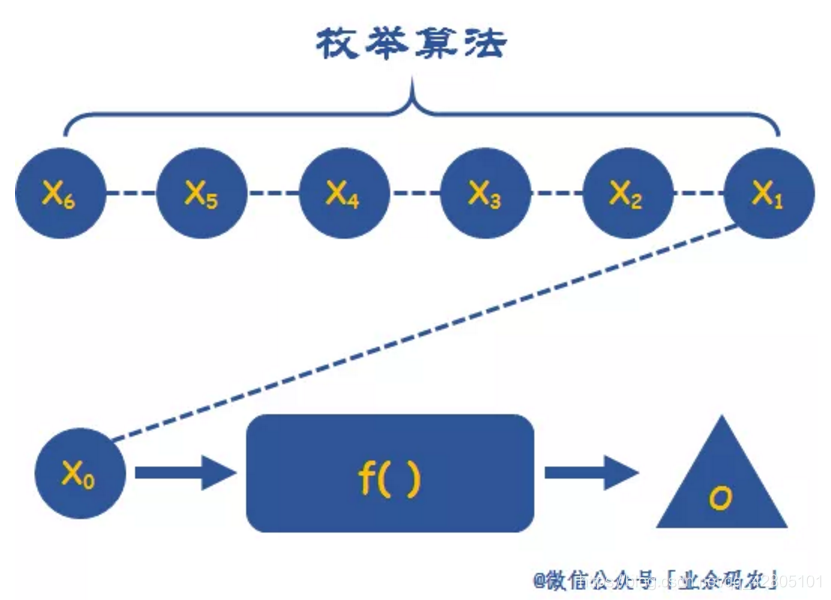
案例：百钱买百鸡问题
公鸡一个五块钱，母鸡一个三块钱，小鸡三个一块钱，现在要用一百块钱买一百只鸡，问公鸡、母鸡、小鸡各多少只？
3.2 递推

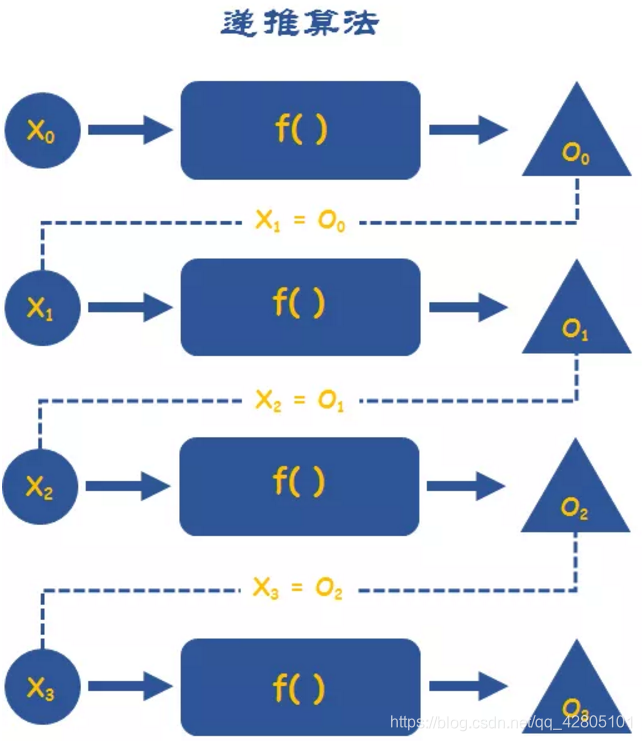
案例：兔子问题
定一对大兔子每月能生一对小兔子，且每对新生的小兔子经过一个月可以长成一对大兔子,具备繁殖能力，如果不发生死亡，且每次均生下一雌一雄，问一年后共有多少对兔子？
3.3 递归

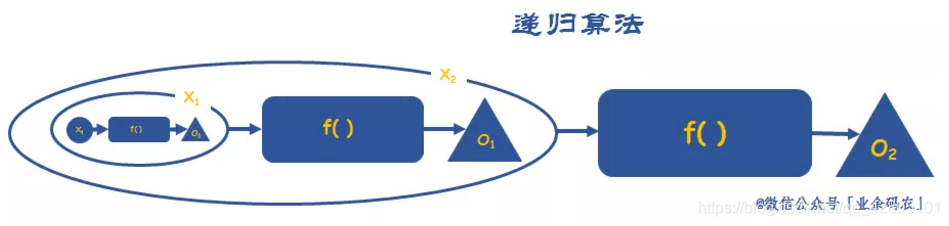
案例：汉诺塔问题
源于印度传说中，大梵天创造世界时造了三根金钢石柱子，其中一根柱子自底向上叠着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定，在小圆盘上不能放大圆盘，在三根柱子之间一次只能移动一个圆盘。
3.4 分治

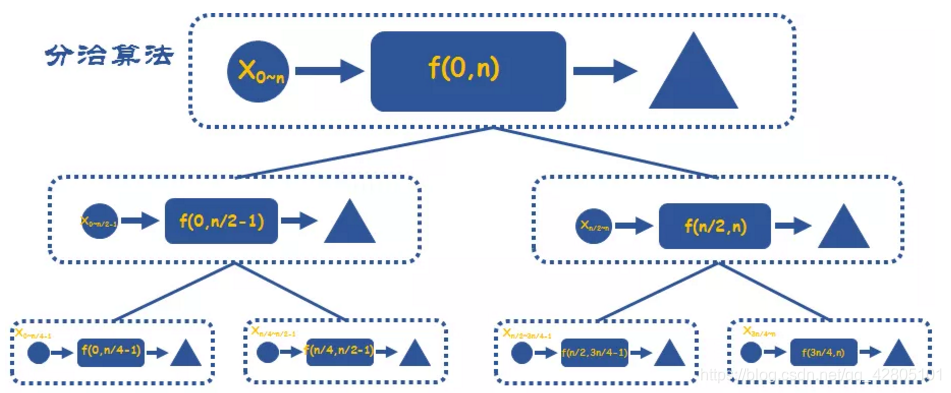
案例：归并排序
3.5 动态规划

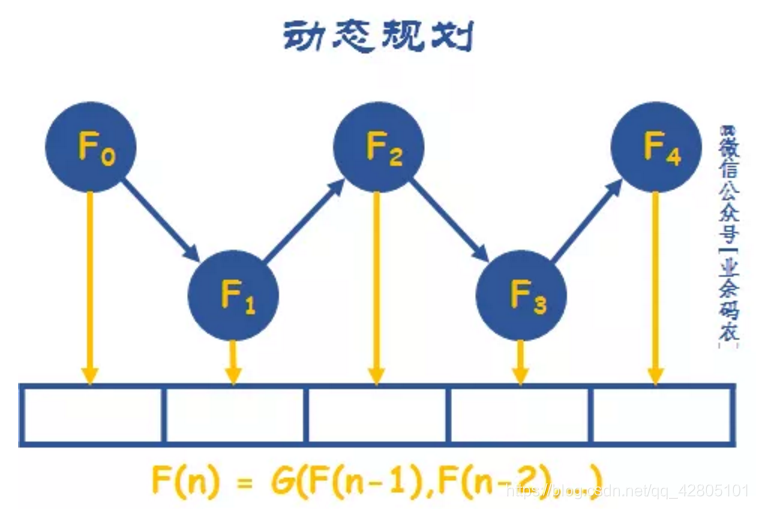
案例：背包问题
有 n 件物品和容量为 m 的背包，给出物品的重量以及价值。求解让装入背包的物品重量不超过背包容量且价值最大 。
3.6 贪心

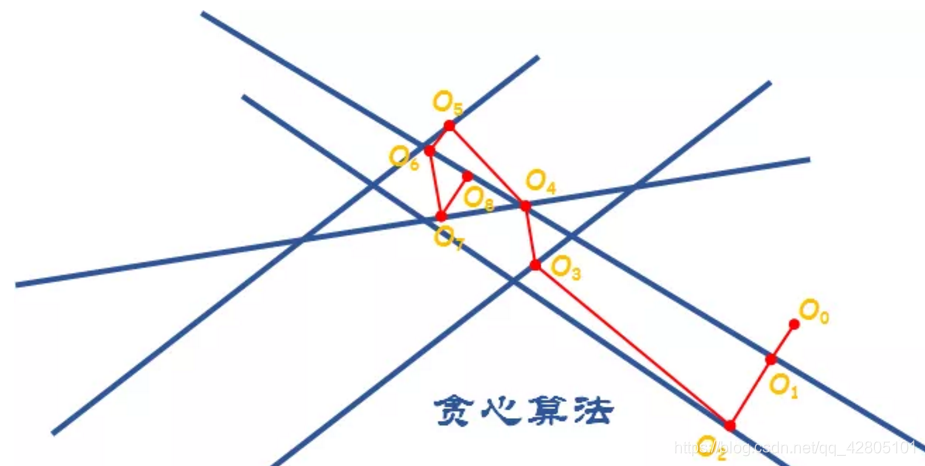
案例：旅行推销员问题
给定一系列城市和每对城市之间的距离，求解访问每一座城市一次并回到起始城市的最短回路。
3.7 回溯

案例：八皇后问题
在8×8格的国际象棋上摆放8个皇后，使其不能互相攻击，即任意两个皇后都不能处于同一行、同一列或同一斜线上，问有多少种摆法。
3.8 模拟

第三章 稀疏数组

好了，不劝退了，从这章开始我们认真学习

1.引入稀疏数组

提到数组，相信大家并不陌生，但稀疏数组是个什么玩意呢，我们先来看下面这个场景

这是一个五子棋棋盘，很容易想到用二维数据来记录棋盘信息，0代表没下，1代表一个人下的棋，2代表另一个人下的。现在要存储当前的棋盘信息，可用二维数组存，但发现一个问题，0很多（没下棋的地方），而下了棋的地方很少，就这样用一个二维数组来存储的话，属实有点浪费空间，我们能不能用一种方法，只记录有用的信息，比如棋盘的大小（行数和列数）、每个棋子的位置，于是稀疏数组来了。

当一个数组中大部分元素为0或为同一个值的数组时，可以使用稀疏数组。稀疏数组第一行记录总行数、总列数、有效数据数，后面几行记录的是每个有效数的行列位置和对应的值。

2.二维数组转稀疏数组

2.1 思路
第一步，遍历原始二维数组得到有效数据个数sum
第二步，根据sum创建稀疏数组sparseArr int[sum+1][3]
第三步，将二维数组中的有效数据存入到稀疏数组中
2.2 代码实现（强烈建议自己先动手，再对比）

public static int[][] toSparseArr(int[][] arr) {//第一步，遍历原始二维数组得到有效数据个数sumint row = arr.length;int col = arr[0].length;int sum = 0;for (int i = 0; i < row; i++) {for (int j = 0; j < col; j++) {if (arr[i][j] != 0) {sum++;}}}//第二步，根据sum创建稀疏数组sparseArr int[sum+1][3]int[][] sparseArr = new int[sum + 1][3];//第三步，将二维数组中的有效数据存入到稀疏数组中//1 稀疏数组第一行赋值sparseArr[0][0] = row;sparseArr[0][1] = col;sparseArr[0][2] = sum;//2 有效数据存入到稀疏数组中int count = 1;for (int i = 0; i < row; i++) {for (int j = 0; j < col; j++) {if (arr[i][j] != 0) {sparseArr[count][0] = i;sparseArr[count][1] = j;sparseArr[count][2] = arr[i][j];count++;}}}System.out.println("遍历输出稀疏数组");for (int i = 0; i < sparseArr.length; i++) {for (int j = 0; j < sparseArr[0].length; j++) {System.out.print(sparseArr[i][j] + " ");}System.out.println();}return sparseArr;}

3.稀疏数组转二维数组

3.1 思路
第一步，根据稀疏数组第一行记录的总行数、总列数创建出二维数组
第二步，从第二行开始，将稀疏数组中的各个有效数赋值给二维数组
3.2 代码实现（强烈建议自己先动手，再对比）

public static int[][] ToTwoArr(int[][] parseArr) {//第一步，根据稀疏数组第一行记录的总行数、总列数创建出二维数组int row = parseArr[0][0];int col = parseArr[0][1];int num = parseArr[0][2];int[][] arr = new int[row][col];//第二步，从第二行开始，将稀疏数组中的各个有效数赋值给二维数组for (int i = 1; i <= num; i++) {int row1 = parseArr[i][0];int col1 = parseArr[i][1];int value = parseArr[i][2];arr[row1][col1] = value;}System.out.println("遍历输出转化后的二维数组");for (int i = 0; i < arr.length; i++) {for (int j = 0; j < arr[0].length; j++) {System.out.print(arr[i][j] + " ");}System.out.println();}return arr;}

第四章 队列

1.队列的简介

队列是一个有序表，可以用数组或链表来实现。遵循先入先出的原则。
它只允许在一端进行插入操作，在另一端进行删除操作。

2.数组模拟队列

2.1 思路
maxSize代表队列的最大长度，因为队列的输入输出是分别从前后端进行的，因此需要两个参数front和rear分别记录队头和队尾的下标，每取出一个数据front++，每存入一个数据rear++，如图所示

2.2 实现代码

public class ArrayQueue {private int maxSize;private int front;private int rear;private int[] arr;public ArrayQueue(int arrMaxSize) {maxSize = arrMaxSize;arr = new int[maxSize];front = -1;rear = -1;}public boolean isFull() {return rear == maxSize - 1;}public boolean isEmpty() {return front == rear;}public void add(int num) {if (isFull()) {throw new RuntimeException("添加失败，队列已满");} else {rear++;arr[rear] = num;}}public int get() {if (isEmpty()) {throw new RuntimeException("获取失败，空队列");} else {front++;return front;}}public void showQueue() {if (isEmpty()) {throw new RuntimeException("空队列");} else {int t = front + 1;while (t <= rear) {System.out.print(arr[t] + " ");t++;}}}public int peek() {if (isEmpty()) {throw new RuntimeException("空队列");} else {return arr[front + 1];}}
}

总结