【数据结构】初入数据结构中的B类树（B Tree , B+ Tree）

本文主要是介绍【数据结构】初入数据结构中的B类树（B Tree , B+ Tree），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

初入数据结构中的B类树（B- Tree , B+ Tree）

如果觉得对你有帮助，能否点个赞或关个注，以示鼓励笔者呢？！博客目录 | 先点这里

前提概念
- 数据域
- 指针域
B树
- 什么是B树(B-树)？
- B树的定义
- B树的特性
- B树的高
B+ 树
- 什么是B+树？
- B+树的定义
- B+树的小特性
- 为什么B+树会替代B树？
为什么需要B树，B+树？
- 引文
- 为什么我们需要B类树？

前提概念

为了更好的理解B类树，我们先来简单的了解一下两个概念

数据域

B类树的结点中有两个区域，一个是数据域，一个是指针域

什么是数据域？

简单的说，B类树中每个结点存储数据的地方，我们就称之为数据域
而数据域中存储的数据通常是一个个的键值对，键值对就分为键(key)和值(value)，这里通常称键为关键字，也通常会将关键字直接指代整个键值对
站在数据库索引的角度，关键字就是用于建立索引的字段值，而对应的值就是该关键字所对应的目的数据，可以是主键信息，也可以指向实际数据的地址，甚至是完整的一行数据

指针域

什么是指针域？

我们知道二叉树在代码的实现中，通常会有两个指针，既左孩子指针和右孩子指针。而这两个指针所在的区域，我们就称之为指针域
而存放左右孩子指针的因为B类树并不是一棵二叉树，它是一棵多叉树。也就说明了，一棵B类树，可能有多个指针，每个的结点的所有的指针所在的区域就是我们说的指针域啦。概念都是一样的。

B树

什么是B树(B-树)？

B-树，即为B树。需要强调的是它们两者都是同一种树，并非两种不一样的树。因为B树的英文名称为B-tree，-实际是杠的意思，但是也就不知怎么的B-tree就被翻译成为B-(减)树。

B树，又名B-树(B减树)。它是一棵多路平衡多路查找树

B树的定义

一棵m阶B树的定义

结点需要满足
(1) 根结点至少有两个孩子结点
(2) 树中每个结点最多有m个孩子结点(m>=2)
(3) 除根结点和叶子结点外，其他所有结点至少要有 ceil(m/2)个孩子
(4) 所有的叶子结点都位于同一层（平衡特性）

关键字需要满足
假设每个非叶子结点中包含n个关键字信息，关键字以k表示，指针以p表示
(1) Ki (i = 1,…,n)某个非叶子结点的关键字，关键字需要满足升序序列排序，k(i-1) < k(i)
(2) 每个非叶子结点中的关键字个数n需要满足 ceil(m/2) -1 <= n <= m - 1
(3) 非叶子结点的指针p[1]…p[m]中

第一个指针，p[1]指向的孩子结点的所有关键字必然小于当前结点k[1]关键字；
最后一个指针，p[m]指向的孩子结点的所有关键字肯定大于当前结点k[m-1]关键字 ;
其他p[i]指向孩子结点所有的关键字必然在当前结点(k[i-1],k[i])的开区间范围内

通俗版解释一下

m就是几阶的含义，m取决结点的容量和相关配置。3阶B树的每个结点分叉数最多为3，最多三个孩子结点
ceil函数是指向上取整的意思，非四舍五入，如ceil(1.5) = 2, ceil(1.2) = 2 ,ceil(3.4) = 4
关键字定义(2) 的意思可以通俗的理解成，每个非叶子结点的关键字个数肯定小于该结点能拥有的孩子结点树，最多就存储m - 1个关键字，最少也要存储ceil(m/2) - 1个
关键字定义(3) 的意思是某结点最左孩子结点的所有关键字肯定小于当前结点最左关键字的值，就像下图的3,5肯定小于8
最右孩子结点的所有关键字肯定大于当前结点的最右关键字 ; 例如下图的13肯定大于12和8
而中间的孩子结点的所有关键字肯定满足于一个当前结点关键字的开区间范围(k[i - 1] , k[i]) , 例如下图的p2孩子结点的9关键字肯定位于(8,12)关键字之间

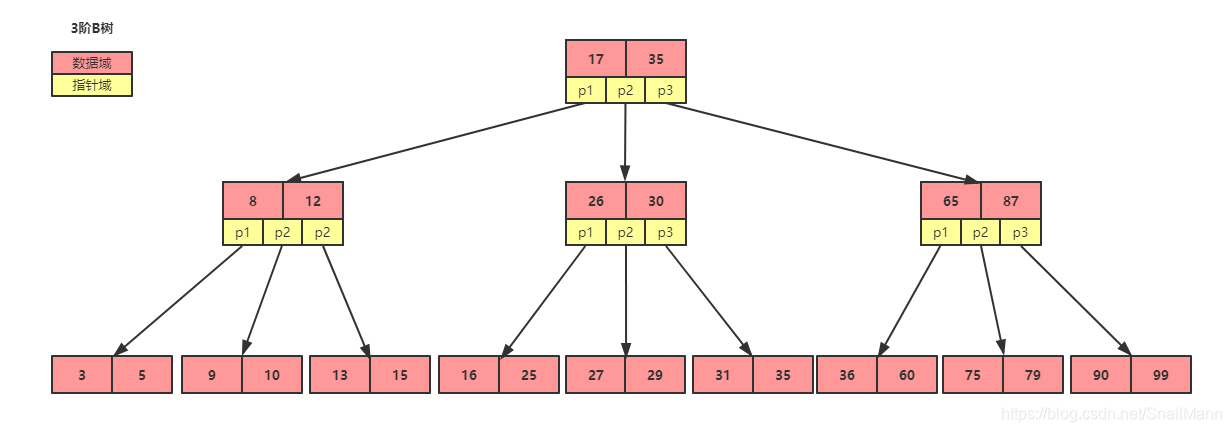
上图是一个3阶B树

总之，我们大致的知道，B树并不是一棵二叉搜索树，而是一颗具有平衡性质的多路查找树。同时B树的定义比较复杂，具有指针域和关键字域的概念，一个结点可以存储多个数据元素，上一段是对结点定义约束，下一段是对结点内部所存储的关键字的约束

B树的特性

关键字集合分布在整棵树中
任何一个关键字出现且只出现在一个结点中
搜索有可能在非叶子结点结束
B树的查找性能基本等价于平衡二叉树的二分查找（不考虑IO的情况下）
可以实现自平衡，让所有叶子结点都在同一个层级

B树的高

现在有一个问题，关键字总数为n的m阶B树的高是多少？

( $log_{ceil(m/2)}{(n+1)/2}$ ) + 1
既底数是ceil(m/2)，最后的对数结果 + 1就是这颗B树的高

引用至@百度百科
在这里插入图片描述

因为求B树，B+树的高的资料的确是有些少，所以看完之后，说实话，我是一脸懵逼的。的确有挺多问题，我都没有理解好，比如说B树含N个关键字，为什么就有N +1个叶子结点呢？这个是怎么推出来的。这个问题可以确定的话，中间步骤还是好理解的。但是…但是后面的归纳还是懵了。

所以，想想算了，时间有限，因为学习性价比，所以还是暂时留给有志之士去解答吧，贫道暂无能为力

B+ 树

什么是B+树？

B+树是一种树型数据结构，通常用于数据库和操作系统的文件系统中。B+树的特点是能够保持数据稳定有序，其插入与修改拥有较稳定的对数时间复杂度。B+树元素自底向上插入，这与二叉树恰好相反。
B+树 - @百度百科

B+树的定义

B+树是B树的变种，其定义基本与B树相同，除了

非叶子结点的子树指针与关键字个数相同，不像B树的关键字数要少于指针数
非叶子结点的子树指针p[i]所指向的孩子结点的所有关键字处于当前结点关键字[k[i],k[i+1])左闭右开的范围区间内
所有的非叶子结点的关键字，都会继承至其中孩子结点中，是其孩子结点元素的最大值或最小值
非叶子结点仅用来索引，数据都保存在叶子结点中
所有叶子结点的数据均有两个链指针分别指向上一个数据和下一个数据，构成双向链表

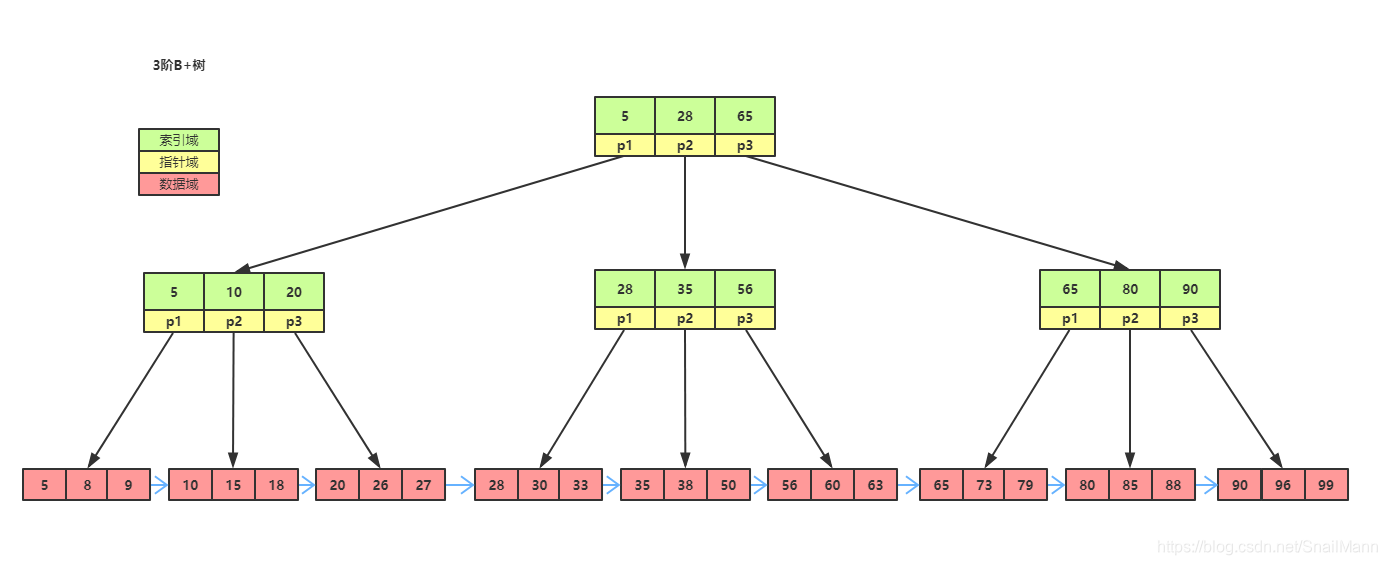
在这里插入图片描述
B树和B+树的区别

B+树，不同于B树的是，所有数据都存储在叶子结点中，非叶子结点不存储任何数据，仅仅是一个索引值。所以B+树查找的时间复杂度非常稳定，都是从根遍历到叶子结点，不会在非叶子结点上中断。

B+树小特性

因为B+树的定义中，所有的非叶子结点的关键字，都会继承至其中孩子结点中，是其孩子结点元素的最大值或最小值，所以就造成了一个特性，根结点的最小值，可能是整棵树的最小值。根结点的最大值可能是整棵树的最大值

举例如下图：

在这里插入图片描述

为什么B+树会替代B树？

总之呢，在数据库索引，文件系统等许多场景中，B+树逐渐替代B树，这是为什么呢？

B+树的磁盘读写代价更低
因为B+树的中间结点存储的都是索引数据，仅仅是一个地址，并非直接的数据，所以同一个结点中（同一个磁盘页大小），B+树可容纳的关键字数会比B树更多（因为一个简单的地址几乎肯定小于一个直接的数据）。所以同样的数据量下，B+树会比B树更加“矮胖”，树高更小，所以查询时需要的IO次数就更少
B+树的查询效率更加稳定
因为B+树的所有元素都存储在叶子结点中，而叶子结点都属于同一层级，每一个B+树查询都是从根结点遍历到叶子结点的过程，所以不管查询什么，时间复杂度相比B树查询都更加的稳定和近似。
B+树更有利对数据的扫描
B树中虽然解决了查询的效率，但是如果需要查询一串相邻的数值，有可能需要回溯来回扫描或是从根结点多次中序遍历。而B+树的所有元素都存储叶子结点，每个叶子结点都有指向下一个结点的指针，直接线性遍历即可。同样B+树也更加的利于做范围查询

为什么需要B树，B+树？

引文

阶段一
在了解为什么需要B类树之前，我们首先来了解一下，我们为什么需要二叉查找树？
在这里插入图片描述
我们为什么需要二叉查找树呢？

简单的说，就是我们想要更快的从一堆数据中，找到我们想要的数据对吧。
一个n长度的线性数据集合，正确情况下的查找，就是一个一个的遍历，时间复杂度是O(n), 所以非常慢，这时候我们就引入了二分查找，时间复杂度就从O(n)骤降到O(logn)，Wow! NiuBei!!

阶段二
我们有了二叉查找树啦，终于可以快速的查找速度了。但是有一天，我们突然的发现这个二叉查找树，也变的很慢很慢？？怎么回事？有Bug吗？！！！
在这里插入图片描述
自平衡二叉查找树
因为二叉查找树的不平衡现象，导致最差的查找结果会退化成O(n)的线性遍历，所以我们要避免出现这么一个情况。于是自平衡二叉树就出现了

自平衡二叉查找树的出现，让二叉查找树在不断的增删查改中得到平衡的维护。总之一句话，就是不会让搜索退化成O(n)的线性遍历，依然保持高性能的O(logn)， Wow! NiuBei!!
当然这个阶段也有很多的分类哈，比如AVL树，红黑树，等等

阶段三

鉴于我知识体系的逐渐丰富，我突然想造个数据库诶，然后陷入造数据库的庞大工程中…
嗯，使用起来还可以诶，我真NiuBi。（一段时间后，数据量大了~~）
Wo Cao! 这有点慢，怎么办？怎么办？
行吧，那就上索引吧，加入索引特性，我的索引就用平衡二叉搜索树来实现吧，之前感觉很良好（AVL树，红黑树等随便一种啦，逃…），
索引新特性上线中
呀，提升不小呀! 至少比以前快了来不少，看来我还是Niu Bei ! (数据量持续增大中~)
Wo Cao! 怎么有索引还这么慢？又出Bug了？
啊，我上索引了，IO操作还这么频繁的嘛？ IO资源都要炸啦！凉凉，看来还是我操作系统基础太差了，不该用平衡二叉树作为索引的底层实现呀！

为什么我们需要B类树？

从上面的引文中，我们知道，当我们使用平衡二叉查找树作为数据库索引的底层实现时，会面临着大量IO操作，从而导致查找性能不佳。

原因一
那么以平衡二叉查找树为底层实现的索引查找为什么会面临这么大量的IO操作呢？

我们知道平衡二叉查找树的本质是一棵二叉树，二叉树的每个结点最多只能有两个孩子结点。树高为n的二叉树最多只能有(2^n) - 1个结点。
也就是说, 一棵高为n的平衡二叉查找树，最多只能存放(2^n) -1个数据的索引。那么我们的数据库如果有1亿的数据量，那么我们索引树的高大概就有27层，2^27 = 1,3421,7728(1亿+)。
当我们要在1亿个数据中查找我们想要的数据，最差的情况下，就要进行27次判断，也就是要进行27次IO操作。 这27次IO操作听上去可能还很少的样子，但是因为磁盘读写速度很慢（不是内存计算呀），所以27次慢速读写累加起来就是一个庞大的耗时操作了。

所以现在我们知道了以平衡二叉查找树为底层实现的索引查找为什么这么慢了。而B树，B+ 树可以远远的降低我们索引树的高度，同样的数据量，因为B树，B+树的一个结点可以容纳很多很多个关键字，同时还可以由很多个孩子结点，从几个到上千个，所以整体索引树的高度可能只有 3~4层 的高。27 ->4 什么概念？简直是削减呀！这就是我们为什么需要B类树的原因之一啦

简单的说，B类树在数据库索引上的应用性能会比平衡二叉搜索高，并不是B类树在设计上就比平衡二叉搜索树牛逼，而是在数据库读写是站在磁盘读写基础上的，追求的是少量的IO操作，而B类树恰好可以做到这一点。
但是如果要换成以内存计算为前提的查找，B类树的性能就不一定要比平衡二叉树要高了，性能甚至会更低。因为内存计算中没有所谓的IO操作。以降低IO操作次数为卖点之一的B类树没有太多的优势可言了。

原因二

我们知道关系型数据库，文件管理系统领域，数据主要是存储在磁盘中的

而磁盘读取数据是以盘块(block)为基本单位的，既磁盘读取数据一个IO操作就读取一个盘块的数据。而我们的B类树一个结点可以存储多个关键字就恰好可以符合这么一个磁盘的特性
想想如果磁盘每一个盘块的数据，恰好对映射到B类树的一个结点中，既每一个结点所存储的关键字量恰好对应一个磁盘盘块的数据。同一个结点中关键字的线性遍历，也不需要在磁盘方面跨盘块进行操作，这样就又省了一笔IO操作

这就是我们为什么需要B类树的原因之二

总结一下

所以我们可以简单的总结一下，为什么在数据库，文件管理系统领域，我们需要使用B类树来替代平衡二叉搜索树成为索引的底层实现，主要就是两个原因：

B类树的一个结点可以存储多个数据，可以有多个分支，所以可以大大的降低正棵树的高度，减少磁盘IO操作
B类树的一个结点可以存储多个数据的特点，恰好也符合了磁盘的物理构造特性，通过将一个结点最多存储对应一个物理盘块的数据，让同结点数据进行线性遍历时，不需要跨盘块进行查询，同样也减少了磁盘查询时间