ARC068F Solitaire

题目:

Problem Statement

Snuke has decided to play with N cards and a deque (that is, a double-ended queue). Each card shows an integer from 1 through N, and the deque is initially empty.

Snuke will insert the cards at the beginning or the end of the deque one at a time, in order from 1 to N. Then, he will perform the following action N times: take out the card from the beginning or the end of the deque and eat it.

Afterwards, we will construct an integer sequence by arranging the integers written on the eaten cards, in the order they are eaten. Among the sequences that can be obtained in this way, find the number of the sequences such that the K-th element is 1 . Print the answer modulo 109+7.

Constraints

• 1≦K≦N≦2,000

Input

The input is given from Standard Input in the following format:
NK

Output

Print the answer modulo 109+7.

Sample Input 1

2 1

Sample Output 1

1

There is one sequence satisfying the condition: 1,2 . One possible way to obtain this sequence is the following:

• Insert both cards, 1 and 2 , at the end of the deque.
• Eat the card at the beginning of the deque twice.

思路:

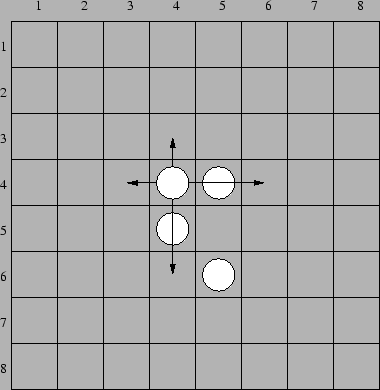
将第一步插入后的序列(插入序列)想象成两个单调递减栈A和B,其中一个栈最小值为1,不妨设这个栈为A.(两个栈按图中线连起来即得到插入序列)

 依次从两个栈中取出元素,得到删除序列.取元素的步骤如图1所示

①从A取出1上全部元素及B中部分元素(可能没有也可能是B中全部元素)

②取出A中的1

③取出B中剩余元素,B中剩余n-k个元素,共种取法.(最后一种元素无论从序列左边取还是右边取都会加到删除序列的最后一个)

问题即为第一步的取法有多少种.

基本思想:动态规划

dp[i][j]表示添加了i个元素,其中最小值为j的删除队列的个数.

i为栈A顶部取出的部分元素及栈B顶部取出的部分元素,顺序不唯一.

j可能是A取出元素的最小值或B取出的元素的最小值,即从栈中取出的最下面一个元素.

可以表示成如图2所示,即从stack1顶部取走部分元素,最后一个为j,从stack2顶部取走部分元素.

考虑这种情况的上一步.

如果上一步是把stack1中的j加入删除队列,即取出j,那么状态转移方程可表示为

如果上一步是将stack2中的元素加入删除队列,由于当前j为最小值,所以上一步最小值也必定为j,即

需要注意此处stack2必须不为空,即j<=n-i+1.

综合来看得到状态转移方程:

初始状态:

代码:

import java.util.Scanner;class Main {static int mod = 1000000007;public static void main(String[] args) {int ans = 0;Scanner in = new Scanner(System.in);int n = in.nextInt();int k = in.nextInt();int[][] dp = new int[n+1][n+1];//初始化状态for(int j = 1;j<=n;j++) {dp[1][j]=1;}//dpfor(int i = 2;i<=k;i++) {int sum = dp[i-1][n];for(int j = n-1;j>=1;j--) {sum=(sum+dp[i-1][j])%mod;if(j<=n-i+1) {dp[i][j]=sum;}}}//乘后n-k个元素的组合ans = (dp[k][1]-dp[k-1][1]+mod)%mod;for(int i = 1;i<=n-k-1;i++) {ans = (ans<<1)%mod;}System.out.println(ans);in.close();}
}

参考:

[1]【ARC068F】Solitaire 【动态规划】_ez_2016gdgzoi471的博客-CSDN博客_arc068f