对流层延迟误差计算

2024-01-13 08:50
文章标签 计算 延迟 误差 对流层

本文主要是介绍对流层延迟误差计算，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

一、写在前面

需要实测气象参数的模型：Saastamoinen模型、Hopfield模型

不需要实测气象参数的模型：UNB模型、UNB3m模型（只需要提供高程、纬度和年积日即可计算对流层延迟量）

一般对流层模型中，将对流层天顶总延迟（ZTD：Zenith Total Delay）分为对流层静力学延迟（ZHD：Zenith Hydrostatic Delay）和对流层湿延迟（ZWD：Zenith Wet Delay）。静力学延迟约占总延迟量的90%，可以通过实测气压和气温来计算，而湿延迟影响因素较多，不太容易估算。

PS：静力学延迟又叫做干延迟 ，非静力学延迟又叫做湿延迟。

二、Saastamoinen模型

代码如下：

/*Saastamoinen模型*/
void Saastamoinen(double elevation, double Phi_u, double h, double *Th, double *Tw)
{const double P0 = 1013.25, e0 = 11.69, T0 = 288.15;double p;//大气压力double e;//水汽压double T;//大气温度/*求大气压力*/p = P0 * pow( (1.0 - 0.0068 / T0 / h) , 5);printf("大气压力p = %.10lf\n",p);/*大气温度*/T = 288.15 - 0.0068 * h;//开尔文温度printf("大气温度T = %.10lf\n",T);/*水汽压e*/if(h > 11000){e = 0;}else{e = e0 * pow((1.0 - 0.0068 * h / T0) , 4);}/*静力学延迟Th*/*Th = 0.002277 * p / (1.0 - 0.00266 * cos(2 * Phi_u * M_PI/180) - 0.00028 * h * 1e-3) ;/*湿延迟Tw*/*Tw = 0.0022768 * (1255.0 / T + 0.05) / (1.0 - 0.00266 * cos(2 * Phi_u * M_PI/180) - 0.00028 * h * 1e-3) * e;printf("静力学延迟Th = %.10lf\n",*Th);
}
//Saastamoinen.h
void Saastamoinen(double elevation, double Phi_u, double h, double *Th, double *Tw);

三、UNB3模型

静力学延迟：

非静力学延迟：

上面参数按照以下公式得出，

Average是年均值，Amplitude是振幅值或者波动值。

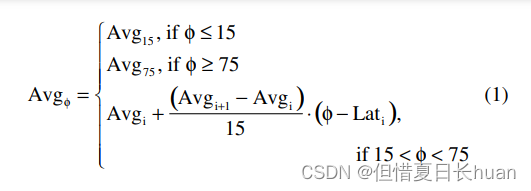
Lati指的是离Φ最近的两个纬度中最小的那个，比如41度的Lati为30度。

参考年积日为28，28日为延迟最小的一天。

Hopfield的精度较差，此处不做说明。UNB3m与UNB3在参数表上有所不同。UNB3的water vapour pressure (WVP)在UNB3m中被换为relative humidity (RH)。

原因：

The version UNB3m was developed to avoid the problematic values of relative humidity. Following the same method of computation as for the pressure and the temperature, average and amplitude for relative humidity were derived from the U.S. Standard Atmosphere Supplements, 1966 [Orliac, 2002].

代码如下：

const double P_avg[5] = {1013.25, 1017.25, 1015.75, 1011.75, 1013.00};//压强年均值
const double T_avg[5] = {299.65, 294.15, 283.15, 272.15, 263.65};//温度年均值
const double e_avg[5] = {26.31, 21.79, 11.66, 6.78, 4.11};//水汽压年均值
//const double e_avg[5] = {75.0, 80.0, 76.0, 77.5, 82.5};
const double Beta_avg[5] = {6.30e-3, 6.05e-3, 5.58e-3, 5.39e-3, 4.53e-3};//温度梯度年均值
const double LambDa_avg[5] = {2.77, 3.15, 2.57, 1.81, 1.55};//水汽梯度年均值const double P_amp[5] = {0.00, -3.75, -2.25, -1.75, -0.50};//压强振幅值
const double T_amp[5] = {0.00, 7.00, 11.00, 15.00, 14.50};//温度振幅值
const double e_amp[5] = {0.00, 8.85, 7.24, 5.36, 3.39};//水汽压振幅值
//const double e_amp[5] = {0.0, 0.0, -1.0, -2.5, 2.5};
const double Beta_amp[5] = {0.00, 0.25e-3, 0.32e-3, 0.81e-3, 0.62e-3};//温度梯度振幅值
const double LambDa_amp[5] = {0.00, 0.33, 0.46, 0.74, 0.30};//水汽梯度振幅值const double k1 = 77.60, k2_l = 16.60, k3 = 377600;
const double g = 9.80665, Rd = 287.054;/*UNB3*/
void UNB3(double Phi, double H, double DOY, double *ZHD, double *ZWD)
{double dh;double T0, P0, e0, Beta, LambDa;double gm, Tm, LambDa_l;/*求5个气象参数*/Coefficient(Phi, DOY, &T0, &P0, &e0, &Beta, &LambDa);//printf("T0 = %.10lf,P0 = %10.lf,e0 = %.10lf,Beta = %.10lf,LambDa = %.10lf\n",T0,P0,e0,Beta,LambDa);LambDa_l = LambDa + 1;gm = 9.784 * (1.0 - 2.66 * 1e-3 * cos(2 * Phi * M_PI/180) - 2.8e-7);Tm = (T0 - Beta * H) * (1.0 - Beta * Rd / gm / LambDa_l);//printf("LambDa = %.10lf\n",LambDa);/*天顶方向的干延迟和湿延迟*/*ZHD = 1e-6 * k1 * Rd / gm * P0 * pow((1.0 - Beta * H / T0) , g / (Rd * Beta));*ZWD = 1e-6 * Rd * (Tm * k2_l + k3) / (gm * LambDa_l - Beta * Rd) * pow((1.0 - Beta * H / T0) , LambDa_l * g / Rd / Beta - 1.0) * (e0 / T0);}/*计算5个气象参数*/
void Coefficient(double Phi, double DOY, double *T0, double *P0, double *e0, double *Beta, double *LambDa)
{double Tem;Tem = cos((DOY - 28) * 2 * M_PI / 365.25);/*求T0 P0 e0 Beta LambDa*/if(Phi<=15){*T0 = T_avg[0] - T_amp[0] * Tem;*P0 = P_avg[0] - P_amp[0] * Tem;*e0 = e_avg[0] - e_amp[0] * Tem;*Beta = Beta_avg[0] - Beta_amp[0] * Tem;*LambDa = LambDa_avg[0] - LambDa_amp[0] * Tem;}if(Phi>15&&Phi<30){*T0 = T_avg[0] + (T_avg[1] - T_avg[0]) / 15 * (Phi - 15) - (T_amp[0] + (T_amp[1] - T_amp[0]) / 15 * (Phi - 15)) * Tem;*P0 = P_avg[0] + (P_avg[1] - P_avg[0]) / 15 * (Phi - 15) - (P_amp[0] + (P_amp[1] - P_amp[0]) / 15 * (Phi - 15)) * Tem;*e0 = e_avg[0] + (e_avg[1] - e_avg[0]) / 15 * (Phi - 15) - (e_amp[0] + (e_amp[1] - e_amp[0]) / 15 * (Phi - 15)) * Tem;*Beta = Beta_avg[0] + (Beta_avg[1] - Beta_avg[0]) / 15 * (Phi - 15) - (Beta_amp[0] + (Beta_amp[1] - Beta_amp[0]) / 15 * (Phi - 15)) * Tem;*LambDa = LambDa_avg[0] + (LambDa_avg[1] - LambDa_avg[0]) / 15 * (Phi - 15) - (LambDa_amp[0] + (LambDa_amp[1] - LambDa_amp[0]) / 15 * (Phi - 15)) * Tem;}if(Phi>=30&&Phi<45){*T0 = T_avg[1] + (T_avg[2] - T_avg[1]) / 15 * (Phi - 30) - (T_amp[1] + (T_amp[2] - T_amp[1]) / 15 * (Phi - 30)) * Tem;*P0 = P_avg[1] + (P_avg[2] - P_avg[1]) / 15 * (Phi - 30) - (P_amp[1] + (P_amp[2] - P_amp[1]) / 15 * (Phi - 30)) * Tem;*e0 = e_avg[1] + (e_avg[2] - e_avg[1]) / 15 * (Phi - 30) - (e_amp[1] + (e_amp[2] - e_amp[1]) / 15 * (Phi - 30)) * Tem;*Beta = Beta_avg[1] + (Beta_avg[2] - Beta_avg[1]) / 15 * (Phi - 30) - (Beta_amp[1] + (Beta_amp[2] - Beta_amp[1]) / 15 * (Phi - 30)) * Tem;*LambDa = LambDa_avg[1] + (LambDa_avg[2] - LambDa_avg[1]) / 15 * (Phi - 30) - (LambDa_amp[1] + (LambDa_amp[2] - LambDa_amp[1]) / 15 * (Phi - 30)) * Tem;}if(Phi>=45&&Phi<60){*T0 = T_avg[2] + (T_avg[3] - T_avg[2]) / 15 * (Phi - 45) - (T_amp[2] + (T_amp[3] - T_amp[2]) / 15 * (Phi - 45)) * Tem;*P0 = P_avg[2] + (P_avg[3] - P_avg[2]) / 15 * (Phi - 45) - (P_amp[2] + (P_amp[3] - P_amp[2]) / 15 * (Phi - 45)) * Tem;*e0 = e_avg[2] + (e_avg[3] - e_avg[2]) / 15 * (Phi - 45) - (e_amp[2] + (e_amp[3] - e_amp[2]) / 15 * (Phi - 45)) * Tem;*Beta = Beta_avg[2] + (Beta_avg[3] - Beta_avg[2]) / 15 * (Phi - 45) - (Beta_amp[2] + (Beta_amp[3] - Beta_amp[2]) / 15 * (Phi - 45)) * Tem;*LambDa = LambDa_avg[2] + (LambDa_avg[3] - LambDa_avg[2]) / 15 * (Phi - 45) - (LambDa_amp[2] + (LambDa_amp[3] - LambDa_amp[2]) / 15 * (Phi - 45)) * Tem;}if(Phi>=60&&Phi<75){*T0 = T_avg[3] + (T_avg[4] - T_avg[3]) / 15 * (Phi - 60) - (T_amp[3] + (T_amp[4] - T_amp[3]) / 15 * (Phi - 60)) * Tem;*P0 = P_avg[3] + (P_avg[4] - P_avg[3]) / 15 * (Phi - 60) - (P_amp[3] + (P_amp[4] - P_amp[3]) / 15 * (Phi - 60)) * Tem;*e0 = e_avg[3] + (e_avg[4] - e_avg[3]) / 15 * (Phi - 60) - (e_amp[3] + (e_amp[4] - e_amp[3]) / 15 * (Phi - 60)) * Tem;*Beta = Beta_avg[3] + (Beta_avg[4] - Beta_avg[3]) / 15 * (Phi - 60) - (Beta_amp[3] + (Beta_amp[4] - Beta_amp[3]) / 15 * (Phi - 60)) * Tem;*LambDa = LambDa_avg[3] + (LambDa_avg[4] - LambDa_avg[3]) / 15 * (Phi - 60) - (LambDa_amp[3] + (LambDa_amp[4] - LambDa_amp[3]) / 15 * (Phi - 60)) * Tem;}if(Phi>=75){*T0 = T_avg[4] - T_amp[4] * Tem;*P0 = P_avg[4] - P_amp[4] * Tem;*e0 = e_avg[4] - e_amp[4] * Tem;*Beta = Beta_avg[4] - Beta_amp[4] * Tem;*LambDa = LambDa_avg[4] - LambDa_amp[4] * Tem;}}

//UNB3.h
void UNB3(double Phi, double H, double DOY, double *ZHD, double *ZWD);
void Coefficient(double Phi, double DOY, double *T0, double *P0, double *e0, double *Beta, double *LambDa);

四、对流层总延迟

根据以上模型算出的皆为对流层天顶延迟，也不需要用到卫星仰角（高度角）。若想算出总延迟，要再乘以映射函数。干延迟乘以干映射函数，湿延迟乘以湿映射函数，再相加。

 

在这里藏一个main函数吧。

#include <stdio.h>
#include <math.h>
#include "Saastamoinen.h"
#include "UNB3.h"
#include "NMF.h"int main() {double Phi = 30.53165278 ;//用户地理纬度double elevation =  0.2326965967;//卫星高度角或卫星仰角double H = 28.2;//用户海拔double DOY[10] = {152, 152 + 300.0/86400, 152 + 600.0/86400, 152 + 900.0/86400, 152 + 1200.0/86400, 152 + 1500.0/86400, 152 + 1800.0/86400,152 + 2100.0/86400, 152 + 2400.0/86400, 152 + 2700.0/86400};//年积日for(int i=0;i<10;i++){UNB3(Phi, H, DOY[i], &ZHD, &ZWD);printf("ZHD = %.10lf,ZWD = %.10lf\n",ZHD,ZWD);//Saastamoinen(elevation,Phi, H, &Th, &Tw);//printf("Th = %.10lf,Tw = %.10lf\n",Th,Tw);}return 0;
}

这篇关于对流层延迟误差计算的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/600890。

相关文章

java实现延迟/超时/定时问题

java实现延迟/超时/定时问题

《java实现延迟/超时/定时问题》：本文主要介绍java实现延迟/超时/定时问题,具有很好的参考价值,希望对大家有所帮助,如有错误或未考虑完全的地方,望不吝赐教... 目录Java实现延迟/超时/定时java 每间隔5秒执行一次,一共执行5次然后结束scheduleAtFixedRate 和 schedu
阅读更多...
Redis实现延迟任务的三种方法详解

Redis实现延迟任务的三种方法详解

《Redis实现延迟任务的三种方法详解》延迟任务（DelayedTask）是指在未来的某个时间点,执行相应的任务,本文为大家整理了三种常见的实现方法,感兴趣的小伙伴可以参考一下... 目录1.前言2.Redis如何实现延迟任务3.代码实现3.1. 过期键通知事件实现3.2. 使用ZSet实现延迟任务3.3
阅读更多...
Python如何计算两个不同类型列表的相似度

Python如何计算两个不同类型列表的相似度

《Python如何计算两个不同类型列表的相似度》在编程中,经常需要比较两个列表的相似度,尤其是当这两个列表包含不同类型的元素时,下面小编就来讲讲如何使用Python计算两个不同类型列表的相似度吧... 目录摘要引言数字类型相似度欧几里得距离曼哈顿距离字符串类型相似度Levenshtein距离Jaccard相
阅读更多...
使用C#代码计算数学表达式实例

使用C#代码计算数学表达式实例

《使用C#代码计算数学表达式实例》这段文字主要讲述了如何使用C#语言来计算数学表达式,该程序通过使用Dictionary保存变量,定义了运算符优先级,并实现了EvaluateExpression方法来... 目录C#代码计算数学表达式该方法很长，因此我将分段描述下面的代码片段显示了下一步以下代码显示该方法如
阅读更多...
Redis延迟队列的实现示例

Redis延迟队列的实现示例

《Redis延迟队列的实现示例》Redis延迟队列是一种使用Redis实现的消息队列,本文主要介绍了Redis延迟队列的实现示例,文中通过示例代码介绍的非常详细,对大家的学习或者工作具有一定的参考学习... 目录一、什么是 Redis 延迟队列二、实现原理三、Java 代码示例四、注意事项五、使用 Redi
阅读更多...
如何用Java结合经纬度位置计算目标点的日出日落时间详解

如何用Java结合经纬度位置计算目标点的日出日落时间详解

《如何用Java结合经纬度位置计算目标点的日出日落时间详解》这篇文章主详细讲解了如何基于目标点的经纬度计算日出日落时间,提供了在线API和Java库两种计算方法,并通过实际案例展示了其应用,需要的朋友... 目录前言一、应用示例1、天安门升旗时间2、湖南省日出日落信息二、Java日出日落计算1、在线API2
阅读更多...
MyBatis延迟加载的处理方案

MyBatis延迟加载的处理方案

《MyBatis延迟加载的处理方案》MyBatis支持延迟加载（LazyLoading）,允许在需要数据时才从数据库加载,而不是在查询结果第一次返回时就立即加载所有数据,延迟加载的核心思想是,将关联对... 目录MyBATis如何处理延迟加载？延迟加载的原理1. 开启延迟加载2. 延迟加载的配置2.1 使用
阅读更多...
poj 1113 凸包+简单几何计算

poj 1113 凸包+简单几何计算

题意： 给N个平面上的点，现在要在离点外L米处建城墙，使得城墙把所有点都包含进去且城墙的长度最短。 解析： 韬哥出的某次训练赛上A出的第一道计算几何，算是大水题吧。 用convexhull算法把凸包求出来，然后加加减减就A了。 计算见下图： 好久没玩画图了啊好开心。 代码： #include <iostream>#include <cstdio>#inclu
阅读更多...
uva 1342 欧拉定理（计算几何模板）

uva 1342 欧拉定理（计算几何模板）

题意： 给几个点，把这几个点用直线连起来，求这些直线把平面分成了几个。 解析： 欧拉定理： 顶点数 + 面数 - 边数= 2。 代码： #include <iostream>#include <cstdio>#include <cstdlib>#include <algorithm>#include <cstring>#include <cmath>#inc
阅读更多...
uva 11178 计算集合模板题

uva 11178 计算集合模板题

题意： 求三角形行三个角三等分点射线交出的内三角形坐标。 代码： #include <iostream>#include <cstdio>#include <cstdlib>#include <algorithm>#include <cstring>#include <cmath>#include <stack>#include <vector>#include <
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2