本文主要是介绍因果推断--PSM的原理和应用(二),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
一、因果推断简要介绍
二、PSM原理
2.1 前提条件
2.2 实施步骤
三、应用案例代码
3.1 自己实现psm
1. 数据读入及各特征显著性检验
2. 建模及添加psm得分
3. 查看实验组和对照组倾向得分的重叠度
4. 用knn为实验组元素匹配样本
5. 对比匹配前后各个特征在实验组、对照组上的Cohen's d效应值、p值
3.2 用psmpy包来实现
1. psm模型初始化并计算psm得分
2. 为实验组匹配元素,并画出匹配后的得分分布
3. 画出匹配前后的效应值差异
4. 其他属性及方法
四、总结
4.1 psm的优缺点
一、因果推断简要介绍
上一篇介绍了DID,本文介绍和DID可一起搭配使用的一种因果推断方法PSM。在正式介绍PSM之前,先来简单回顾一下为什么需要因果推断以及如何做因果推断。我们都知道相关非因果,比起相关我们更希望知道两个事件之间的因果关系,有了确切的因果关系,才能知道对A如何操作才能引起B的变化。解决因果推断问题,目前主要有两种框架,Rubin虚拟事实模型和Pearl因果图模型。站在数据分析的角度上,Rubin虚拟事实模型更容易理解,其核心思想是寻找恰当的对照组。想要知道策略干预带来的效果是多少,我们需要知道该用户在干预和未干预下的表现,但同一时间内无法观测到一个用户的两种状态,所以我们就需要借助AB实验或者构造合适对照组的方式来进行评估。除了AB实验外常用的方法有:双重差分、倾向得分匹配、合成控制、断点回归、双重机器学习、因果随机森林、Uplift Model等。
二、PSM原理
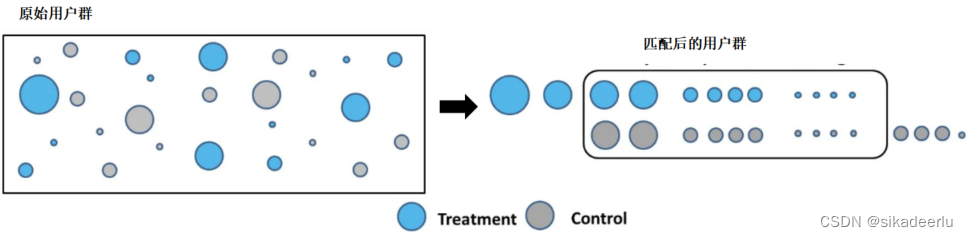
PSM的核心思想是从未受干预的用户群体中,找到和干预对象一模一样的用户,这样就可以把因果效应归因到干预上。一般来说,每个样本有多个特征,对于一个用户来说有:画像特征、行为特征等,如果每个特征都进行匹配,则维度会很多,匹配也会很困难。所以可引进倾向得分P(x)来代替,这样就可以用一维变量进行匹配,从而大大降低匹配的复杂度。
这里个体的倾向得分是指在个体情况一定的前提下,进入处理组的概率。倾向得分可用分类模型得到,选择尽可能多的协变量,类似于回归中的控制变量。计算倾向得分类似于降维的过程,把非常多的协变量维度降为一个维度,就是倾向得分。两个个体的倾向得分非常接近,并不意味着这两个个体的其他属性也接近,这不好判断。不过根据PSM的原理,倾向得分接近就够了,其他属性也接近更好。匹配后可进一步验证其他属性是否更接近了。
2.1 前提条件
(1)样本量要足够大,如果太小,很多干预组的样本可能在控制组匹配不到对象,或者能匹配但是距离很远,也就是匹配度不高。
(2)干预组与控制组的倾向得分要有较大的共同取值范围,否则会丢失较多样本,导致匹配的样本不具代表性。
2.2 实施步骤
1. 倾向得分计算:因变量为是否被干预,自变量为用户特征,建立LR/XGB/RF等模型预测用户进入干预组的概率,以该概率作为倾向得分,也可以其Logit( ln(e(x)/1-e(x) )作为倾向得分。
2. 倾向得分匹配:为干预组用户,在非干预组中匹配一个近似相同的用户,作为对照组
a. 修剪:去除掉倾向得分比较极端的用户,常见的做法是保留得分在[a, b]这个区间的用户。实验组和对照组得分区间的交集,只保留区间中部的90%或95%,如原始得分在[0.05, 0.95]的用户。
b. 匹配:实验组和对照组用户根据得分进行匹配。常用方法有knn和radius,knn即对实验组进行1对k有放回或无放回匹配。radius:对实验组用户,匹配所有得分差异小于radius的用户。
c. 设置得分差异上限:当我们匹配用户时,要求每一对用户的得分差异不超过指定的上限。
3. 平衡性检验:用Cohen’s d效应量衡量匹配后的实验组和对照组在各个特征上的差异,其计算公式如下:
该值的分子为实验组和对照组平均值之差,分母为两组的汇总方差,一般该值不超过0.2则认为匹配通过平衡性检验。
4. 因果效应估计:我们的目标是计算策略干预组的ATT(Average Teamtment Effect on then Treated)。可用匹配到的干预组和对照组计算核心指标的提升情况,从而得到因果效应。
三、应用案例代码
3.1 自己实现psm
1. 数据读入及各特征显著性检验
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import math# 1. 引入数据
df = pd.read_csv('./data/groupon.csv')df.head()
# 2. 查看实验组/对照组各特征的均值
df.groupby('treatment').count()
df.groupby('treatment').mean()# 3. 实验组/对照组各特征差异显著性
df_control = df[df.treatment==0]
df_treatment = df[df.treatment==1]# 以 revenue 为例
from scipy.stats import ttest_ind# 查看两组的均值
print(df_control.revenue.mean(), df_treatment.revenue.mean()) # t检验
_, p = ttest_ind(df_control.revenue, df_treatment.revenue)
print(f'p={p:.3f}')# 输出是否差异是否显著
alpha = 0.05 # 显著水平设为 0.05
if p > alpha:print('两者分布无差异(没有足够的证据拒绝原假设)')
else:print('两者分布差异显著(拒绝原假设)')2. 建模及添加psm得分
a. 建立逻辑回归模型
# 1. 模型数据准备
X = df[['prom_length', 'price', 'discount_pct', 'coupon_duration', 'featured', 'limited_supply']]
y = df['treatment']# 2. 建立逻辑回归模型,预测用户进入干预组的概率
from sklearn.linear_model import LogisticRegression
lr = LogisticRegression()
lr.fit(X, y)# 查看逻辑回归模型各个特征的系数
coeffs = pd.DataFrame({'column':X.columns.to_numpy(),'coeff':lr.coef_.ravel(),
})
coeffsb. 添加psm得分
# 3. 添加倾向匹配得分
df['ps'] = pred_prob[:, 1]# 添加logit后的得分
def logit(p):logit_value = math.log(p / (1-p))return logit_valuedf['ps_logit'] = df.ps.apply(lambda x: logit(x))df.head()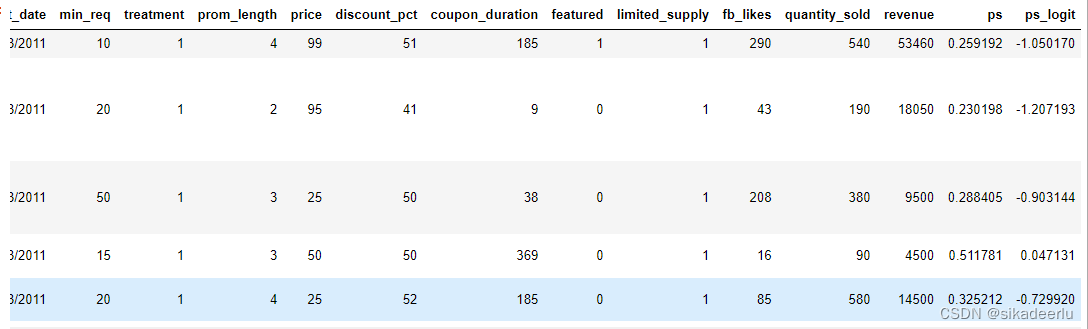 3. 查看实验组和对照组倾向得分的重叠度
3. 查看实验组和对照组倾向得分的重叠度
sns.histplot(data=df, x='ps', hue='treatment')
可以看到实验组和对照组的倾向得分在0.05-0.6之间有较多的重合,所以可进行匹配。
4. 用knn为实验组元素匹配样本
a. 首先为每个元素都进行knn,匹配得分范围在25%标准差内的10个最近的元素
from sklearn.neighbors import NearestNeighbors# 1. 以ps得分标准差的25%作为半径,匹配相邻的10个元素,半径越大或者k越大,可匹配到的元素越多
n_neighbors = 10
caliper = np.std(df.ps) * 0.25
print(f'caliper (radius) is: {caliper:.4f}')# 2. knn
knn = NearestNeighbors(n_neighbors=n_neighbors, radius=caliper)ps = df[['ps']]
knn.fit(ps)# 3. 返回每个点相邻点的索引和距离
distances, neighbor_indexes = knn.kneighbors(ps) print(neighbor_indexes.shape) # 输出neighbor_indexes的长度# 查看第一个元素的匹配结果
print(distances[0])
print(neighbor_indexes[0])b. 为实验组中的每个元素,在对照组中找到一个和它匹配的
matched_control = [] # 保存对照组中匹配到的观测对象for current_index, row in df.iterrows(): # 遍历 dataframe中的每行记录if row.treatment == 0: # 如果当前行是对照组df.loc[current_index, 'matched'] = np.nan # 将匹配到的对象设置为nanelse: for idx in neighbor_indexes[current_index, :]: # 遍历实验组样本的10个相邻元素# 确保当前行不在10个相邻元素中,既排除自己# 并且确保相邻元素在对照组中if (current_index != idx) and (df.loc[idx].treatment == 0):if idx not in matched_control: # 当前对象没有被匹配过df.loc[current_index, 'matched'] = idx # 记录当前的匹配对象matched_control.append(idx) # 并将其插入到待保存的数组中breakdf.head()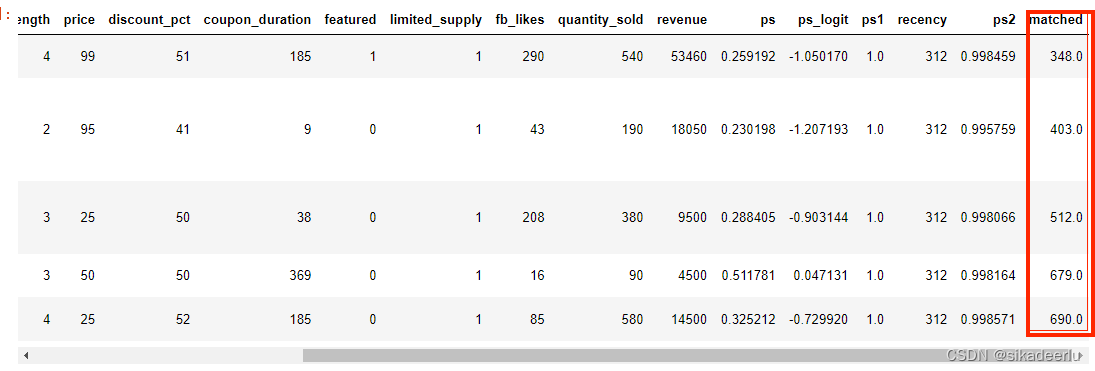
5. 对比匹配前后各个特征在实验组、对照组上的Cohen's d效应值、p值
from numpy import mean
from numpy import var
from math import sqrt# 计算Cohen's d 的方法
def cohen_d(d1, d2):# 计算样本数量n1, n2 = len(d1), len(d2)# 计算样本方差s1, s2 = var(d1, ddof=1), var(d2, ddof=1)# 计算两者的组合方差s = sqrt(((n1 - 1) * s1 + (n2 - 1) * s2) / (n1 + n2 - 2))# 计算均值u1, u2 = mean(d1), mean(d2)# 得到效应值return (u1 - u2) / seffect_sizes = []
cols = ['prom_length', 'price', 'discount_pct', 'coupon_duration', 'featured','limited_supply']for cl in cols:_, p_before = ttest_ind(df_control[cl], df_treatment[cl])_, p_after = ttest_ind(df_matched_control[cl], df_matched_treatment[cl])cohen_d_before = cohen_d(df_treatment[cl], df_control[cl])cohen_d_after = cohen_d(df_matched_treatment[cl], df_matched_control[cl])effect_sizes.append([cl,'before', cohen_d_before, p_before])effect_sizes.append([cl,'after', cohen_d_after, p_after])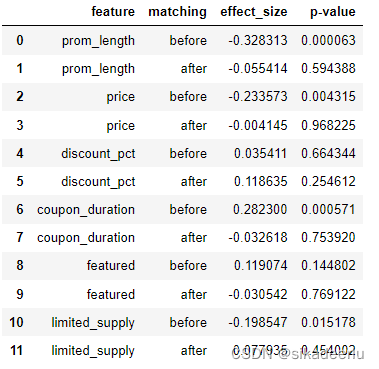
可以看到匹配后除了 discount_pct 这个特征外,其余特征的 Cohen's d 效应值都有所下降,且p值都大于0.05,说明匹配后的这些特征的分部较为均衡,无显著差异。
用柱状图更直观的输出各特征Cohen's d 效应值的前后差异
# discount_pct and featured are not significant, all other features are more balanced after matching
fig, ax = plt.subplots(figsize=(15, 5))
sns.barplot(data=df_effect_sizes, x='effect_size', y='feature', hue='matching', orient='h')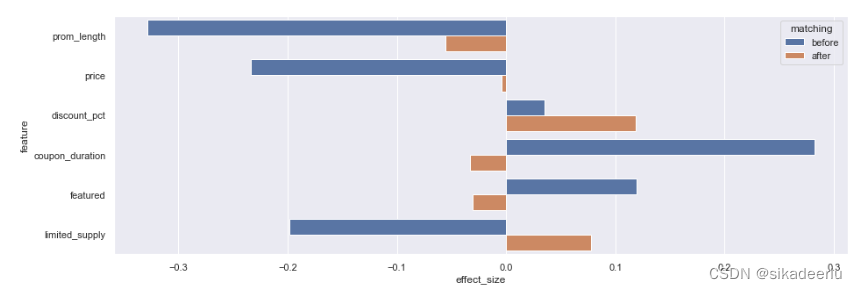
3.2 用psmpy包来实现
1. psm模型初始化并计算psm得分
from psmpy import PsmPy
from psmpy.plotting import *df_psmpy = pd.read_csv('./data/groupon.csv')
df_psmpy.info()# 初始化
# exclude: 模型拟合时要忽略的字段
# indx: 唯一值
psm = PsmPy(df_psmpy, treatment='treatment', indx='deal_id', exclude = ['min_req', 'start_date', 'fb_likes', 'quantity_sold', 'revenue'])# 计算logit得分
psm.logistic_ps(balance=True) # balance=False 建模时是否让实验组和对照组的记录数保持平衡
psm.predicted_data # 查看进入模型中的数据

2. 为实验组匹配元素,并画出匹配后的得分分布
# knn 1:1 匹配
psm.knn_matched(matcher='propensity_logit', replacement=False, caliper=None)# 画出倾向得分的分布图
# x轴是倾向得分,y轴是匹配到的数量
psm.plot_match(Title='Matching Result', Ylabel='# of obs', Xlabel= 'propensity logit', names = ['treatment', 'control']) 
3. 画出匹配前后的效应值差异
# 画出各个特征在匹配前后的效应值
psm.effect_size_plot() 
4. 其他属性及方法
# 输出匹配到的id
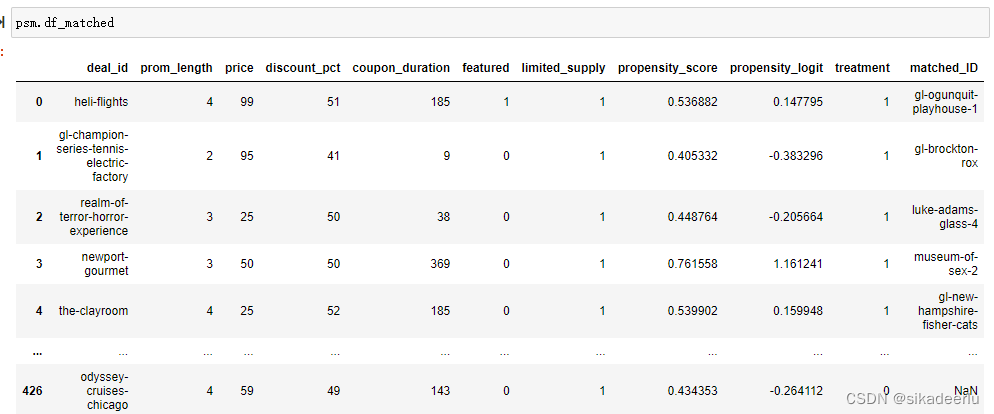
psm.matched_ids# 输出匹配到的原始数据
psm.df_matched# 输出匹配前后的效应值
psm.effect_size# 单独使用
from psmpy.functions import cohenD
cohenD(df_psmpy, treatment = 'treatment', metricName = 'prom_length')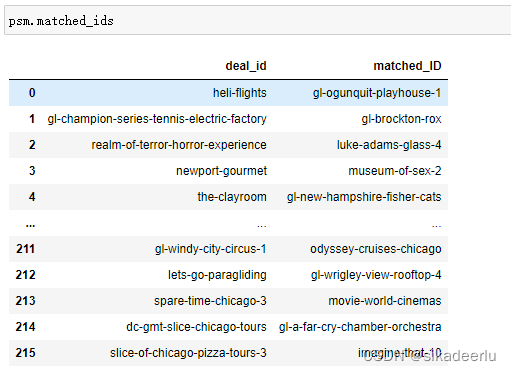


四、总结
4.1 psm的优缺点
优点:psm能够得到和实验组较为相似的对照组,配合DID进行平衡性检验后,能够得到较为可信的因果效应,整体实现起来也较为简单。
缺点:
- 只能缓解由观测变量带来的内生性问题,无法处理由非观测变量产生的内生性问题。
- 对照组需要有足够大的样本量,要不然匹配时会丢失较多样本,导致匹配结果不具有代表性。这个是硬伤。。
这篇关于因果推断--PSM的原理和应用(二)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








