二维点集的凸包点寻找算法

本文主要是介绍二维点集的凸包点寻找算法，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

1. 思路

利用凸凹最直接的性质去判断，即：两个相近的凸点组成的直线，将会把他们的近邻点完全隔离在直线的同一侧。如此一来，先选取一个明显的凸点，如y坐标最小的点，以它为出发点，贪婪式搜寻即可。

如下图所示：

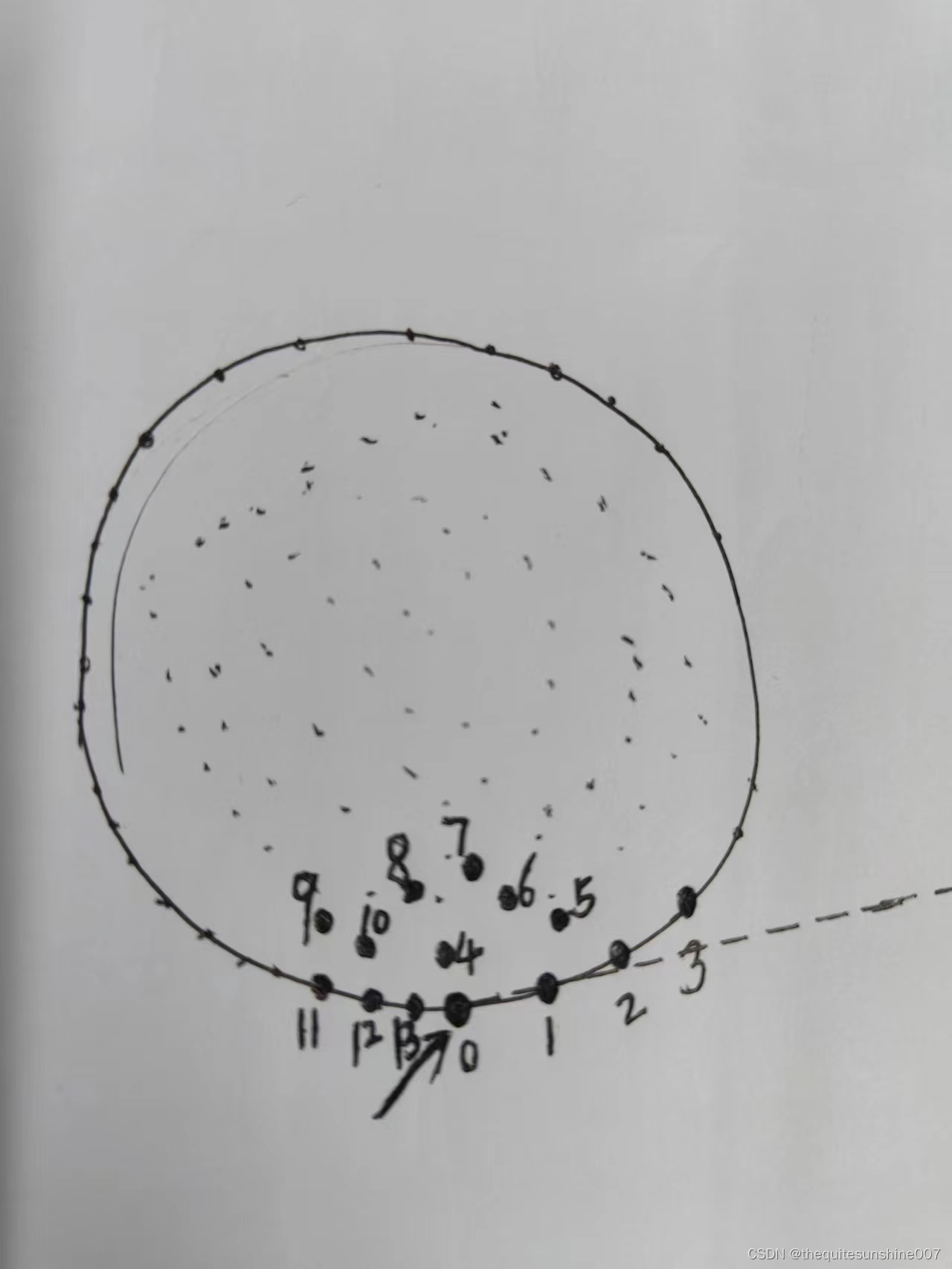
假设0点为y坐标最小的点，图中带编号的点为其近邻点（kd-tree加速查找），遍历编号1~13的点，当遍历到点1时，点0点1组成的直线将点2~点13完全隔离在直线同一侧（条件），满足这个条件后，将点1作为下一轮的出发点，重复上述过程即可。

2. 代码实现

节选， 最终找到的凸点点集索引存在bound_points_map中。

  pcl::KdTreeFLANN<Point> kdtree;kdtree.setInputCloud(points_2d);int prev_idx = -1;unordered_map<int, int> bound_points_map;while (prev_idx != cur_idx){if (bound_points_map.find(cur_idx) != bound_points_map.end())break;else{boundary_points_idx.push_back(cur_idx);bound_points_map.emplace(cur_idx, cur_idx);}auto se

这篇关于二维点集的凸包点寻找算法的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---