本文主要是介绍Minitab的单因子方差分析的结果,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
单因子方差分析概述
当有一个类别因子和一个连续响应并且想要确定两个或多个组的总体均值是否存在差异时,可使用 单因子方差分析。如果经检验,发现至少有一组存在差异,请使用单因子方差分析中的比较对话框来标识存在显著差异的组对。
例如,地毯制造商想要确定几种类型的地毯的耐久性是否存在差异。
要执行单因子方差分析,请选择菜单:统计 > 方差分析 > 单因子。
何时使用备择分析
- 如果具有两个或更多固定类别因子,则在具有所有固定因子时使用拟合一般线性模型,或在具有随机因子时使用拟合混合效应模型。
- 如果标绘一个连续(数值)预测变量和一个连续响应之间的关系,请使用拟合线图
- 如果有多个预测变量,请使用拟合回归模型。
数据注意事项
为了确保结果有效,请在收集数据、执行分析和解释结果时考虑以下准则。
- 数据应当仅包括一个作为固定因子的类别变量。
- 响应变量应当是连续变量。如果响应变量是类别变量,则模型不太可能满足分析假定、准确描述数据或者进行有用的预测。
- 样本数据应当来自正态总体,或者每个样本的数量应当大于 15 或 20。如果样本数量大于 15 或 20,则检验对于偏斜的非正态分布表现得非常好。如果样本数量小于 15 或 20,则对于非正态分布来说,结果可能会具有误导性。
- 每个观测值都应当独立于所有其他观测值。如果观测值是相关的,则结果可能无效,请转到分析重复测量设计。
- 使用最佳做法收集数据。
- 模型应当提供良好的数据拟合。
单因子方差分析示例
某化学工程师想要比较四种油漆混料的硬度。每种油漆混料取六份样品涂到一小块金属上,待金属块凝固后再测量每种样品的硬度。为了检验均值是否相等,并评估均值对之间的差分,分析师配合使用单因子方差分析和多重比较。数据如下表:
| 油漆 | 硬度 | 温度 | 操作员 |
| 配方 2 | 14.9 | 30.3 | 1 |
| 配方 3 | 13 | 30.9 | 2 |
| 配方 4 | 15 | 30.5 | 2 |
| 配方 1 | 17 | 29.4 | 3 |
| 配方 1 | 13.9 | 30 | 3 |
| 配方 3 | 16.4 | 29.6 | 1 |
| 配方 1 | 10.4 | 29.6 | 2 |
| 配方 2 | 3.2 | 29.9 | 2 |
| 配方 2 | 1.9 | 28.9 | 2 |
| 配方 2 | 7.3 | 28.6 | 1 |
| 配方 4 | 17.8 | 30.8 | 3 |
| 配方 2 | 9.6 | 30.8 | 3 |
| 配方 4 | 22.9 | 28.9 | 1 |
| 配方 4 | 17.4 | 30.6 | 3 |
| 配方 3 | 13.3 | 29.8 | 3 |
| 配方 1 | 19.3 | 30 | 1 |
| 配方 1 | 16.1 | 29.9 | 3 |
| 配方 3 | 6.5 | 30.6 | 2 |
| 配方 1 | 11.7 | 30.1 | 3 |
| 配方 4 | 16.9 | 30.7 | 3 |
| 配方 4 | 18.4 | 29.9 | 1 |
| 配方 3 | 11.9 | 29.5 | 2 |
| 配方 2 | 14.5 | 29.9 | 1 |
| 配方 3 | 16.8 | 29.9 | 3 |
对上述数据进行单因子分析,对话框设置如下,同时“比较”选择“Tukey”的方式:
主要结果分析
主要输出包含 p 值、组图、组比较、R2 和残差图。
步骤 1:确定组均值之间的差分在统计意义上是否显著
要确定均值之间的任何差值在统计意义上是否显著,请将 p 值与显著性水平进行比较以评估原假设。原假设声明总体均值均相等。通常,显著性水平(用 α 或 alpha 表示)为 .05 即可。显著性水平 .05 指示在实际上不存在差异时得出存在差异的风险为 5%。
P 值 ≤ α:一些均值之间的差值在统计意义上显著
如果 p 值小于或等于显著性水平,则否定原假设并得出并非所有总体均值都相等的结论。使用您的专业知识可以确定差值实际上是否显著。
P 值 > α:均值之间的差值在统计意义上不显著
如果 p 值大于显著性水平,则您没有足够的证据否定原假设(总体均值相等)。请确认检验具有足够的功效来检测在实际意义上显著的差值
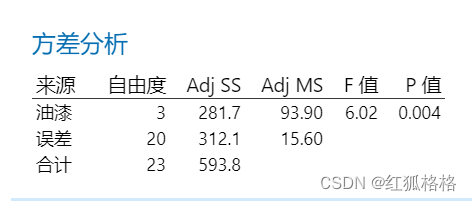
主要结果:P 值
在这些结果中,原假设表明 4 种不同的油漆的硬度均值相等。因为 p 值小于显著性水平 0.05,则可以否定原假设并得出部分油漆的均值不同。
步骤 2:检查组均值
使用区间图可显示每个组的均值和置信区间。区间图显示如下内容:
- 每个点号都代表样本均值。
- 每个区间针对组均值具有 95% 的置信区间。组均值位于组的置信区间内的置信度为 95%。
重要信息:请谨慎解释这些区间,因为进行多重比较时出现类型 1 错误的比率会增加。也就是说,当您增加比较数后,至少有一个比较将错误得出其中一个观测差分会显著不同的概率也会相应增加。

在区间图中,混料 2 具有最低均值,混料 4 具有最高均值。从图形中不能确定任何差分是否在统计意义上显著。要确定统计显著性,请评估均值差分的置信区间。
步骤 3:比较组均值
如果单因子方差分析 p 值小于显著性水平,您将知道部分组均值是不同的,但组对的情况并非如此。针对均值差分使用分组信息表和检验可确定特定组对之间的均值差分是否在统计意义上显著,并且根据差异程度进行估计。
- 分组信息表
使用分组信息表可快速确定任何组对之间的均值差值在统计意义上是否显著。不共享字母的组存在显著差异。
- 均值差分检验
使用置信区间可确定差分的可能范围并确定差分是否具有实际显著性。表格会显示均值对之间差分的一组置信区间。均值差分的区间图会显示相同的信息。不包含零的置信区间表示统计意义显著的均值差分。
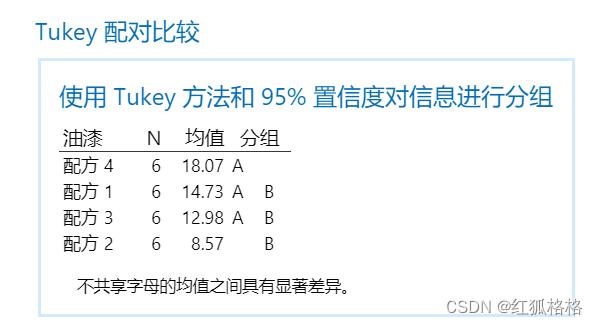
主要结果:均值、分组
在这些结果中,表显示组 A 包含混料 1、3 和 4,组 B 包含混料 1、2 和 3。混料 1 和混料 3 处于两个组中。共享一个字母的均值之间的差分在统计意义上不显著。混料 2 和混料 4 不共享一个字母,这表明混料 4 的均值比混料 2 的均值明显高很多。
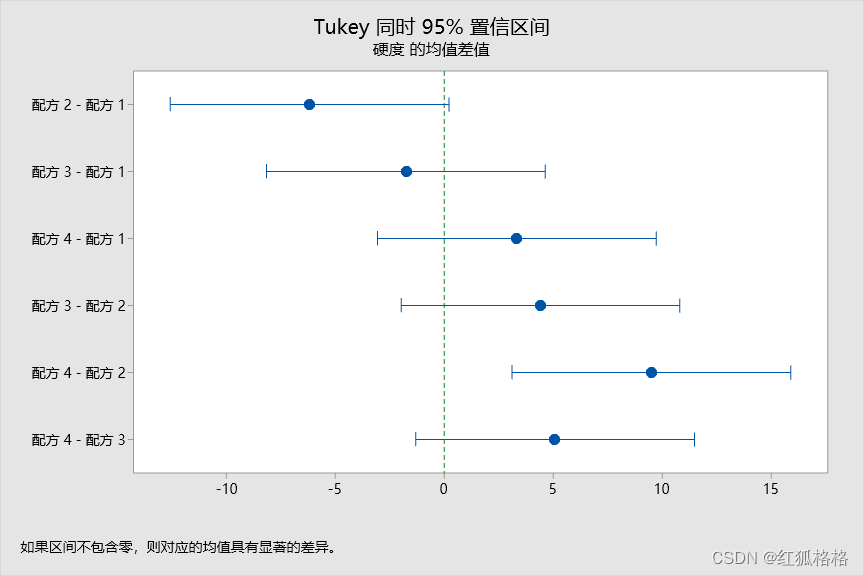
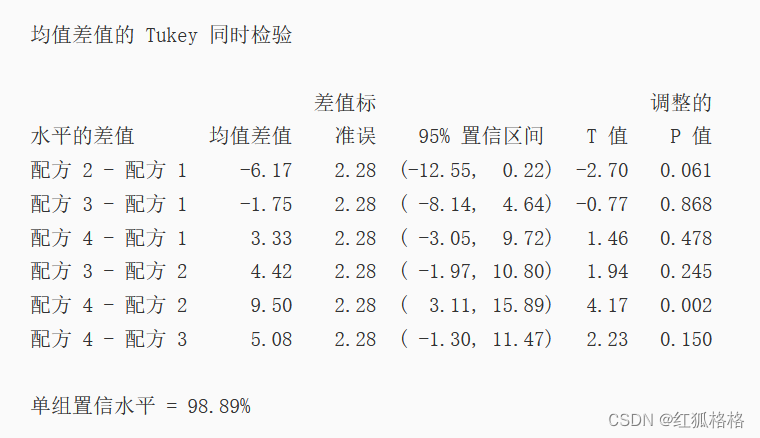
主要结果:整体置信水平 95% CI,单个置信水平
在 Tukey 结果中,置信区间指示如下内容:
- 混料 2 和 4 的均值之间差分的置信区间为 3.11 到 15.89。此范围不包含零,表明这些差分在统计意义上显著。
- 其余均值对的置信区间都包括 0,表明这些差分在统计意义上不显著。
- 95% 的整体置信水平表明所有置信区间包含实际差分的置信度可能是 95%。
- 该表指示单个置信水平为 98.89%。此结果表明每个单个区间包含特定组均值对之间实际差分的置信度可能为 98.89%。每个比较的单个置信水平会针对所有六种比较产生 95% 的整体置信水平。
步骤 4:确定模型与数据拟合的程度
- S
使用 S 可评估模型描述响应值的程度。S 以响应变量的单位进行度量,它表示数据值与拟合值的距离。S 值越低,模型描述响应的程度越高。但是,自身低 S 值并不表明模型符合模型假设。应检查残差图来验证假设。
- R-sq
R2 是由模型解释的响应中的变异百分比。R2 值越高,模型拟合数据的优度越高。R2 始终介于 0% 和 100% 之间。高 R2 值表示模型不符合模型假设。您应检查残差图来验证假设。
- R-Sq(预测)
使用预测的 R2 可确定模型对新观测值的响应进行预测的程度。具有较大预测 R2 值的模型的预测能力也较出色。
实质上小于 R2 的预测的 R2 可能表明模型过度拟合。在向总体中添加不太重要的影响项的情况下,可能会发生过度拟合模型。模型针对样本数据而定制,因此可能对于总体预测不太有效。
在比较模型方面,预测的 R2 还可能比调整的 R2 更有效,因为它是用模型计算中未包含的观测值计算得出的。

主要结果:S、R-sq、R-sq(预测)。在这些结果中,因子对响应中 47.44% 的变异给出了解释。S 表示数据点和拟合值之间的标准差约为 3.95 个单位。
步骤 5:确定模型是否符合分析的假设条件
使用残差图可帮助您确定模型是否适用并符合分析的假设。如果不符合此假设,则模型可能无法充分拟合数据,在解释结果时应当格外小心。
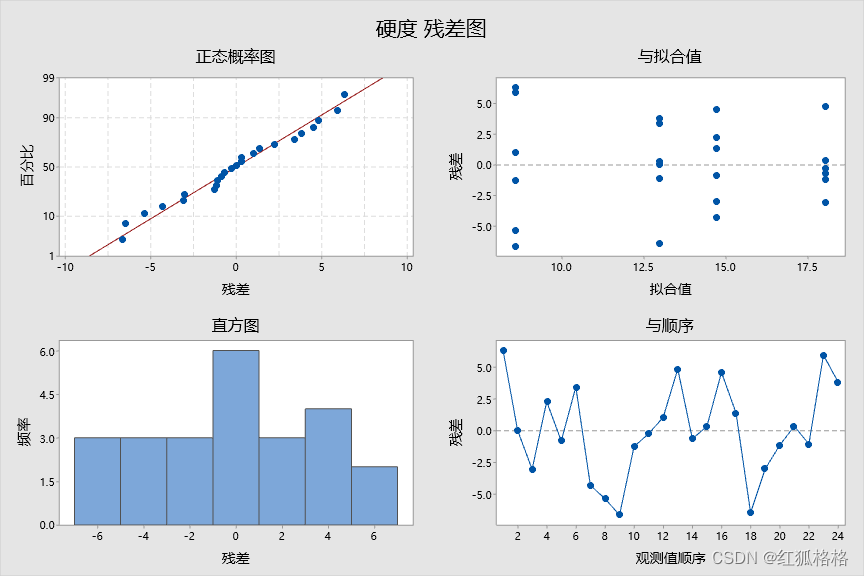
残差与拟合值图
使用残差与拟合值图可验证残差随机分布和具有常量方差的假设。理想情况下,点应当在 0 的两端随机分布,点中无可辨识的模式。
下表中的模式可能表示该模型不满足模型假设。
| 模式 | 模式的含义 |
|---|---|
| 残差相对拟合值呈扇形或不均匀分散 | 异方差 |
| 远离 0 的点 | 异常值 |
在此残差图与拟合图中,点随机散落在图上。没有组看起来具有明显不同的变化,并且没有明显的异常值。
残差与顺序图
使用残差与顺序图可验证残差独立于其他残差的假设。当以时序显示时,独立残差不显示趋势或模式。点中的模式可能表明,彼此相近的残差可能相关联,因此并不独立。理想情况下,图中的残差应围绕中心线随机分布。

如果查看模式,便可查出原因。下列类型的模式可能表明残差属于依赖项。
趋势: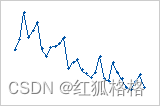 偏移:
偏移: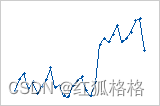 周期:
周期:
在此残差与顺序图中,残差似乎会围绕中心线随机衰减。
残差的正态概率图
使用残差正态概率图可验证残差呈正态分布的假设。残差的正态概率图应该大致为一条直线。下表中的模式可能表示该模型不满足模型假设。
| 模式 | 模式的含义 |
|---|---|
| 非直线 | 非正态性 |
| 远离直线的点 | 异常值 |
| 斜率不断变化 | 未确定的变量 |
注意:如果单因子方差分析设计符合样本数量原则,则结果不会受正态性偏离的显著影响。
在此正态概率图中,残差通常看起来是一条直线。从残差图与拟合图中,可以看到四个组中的每一个都具有六个观测值。由于此设计不符合样本数量规则,所以满足正态假设很重要,因而检验结果是可靠的。
这篇关于Minitab的单因子方差分析的结果的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




