本文主要是介绍因果推断笔记1基础符号及表述,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
1 当发生事件a时 产生结果Y
假设 a {0,1} 0为未发生事件a 1为发生, Y {0,1} 0为未产生结果Y 1为产生
则 为未发生事件a 观测到Y产生
为发生事件a 观测到Y产生
为发生事件a 未观测到Y产生
注:对于个体事件 即a是否发生对Y没有啥影响则不存在因果关系,反之亦然。
所以个体存在因果关系可表述为
2 当所有个体都发生事件a或不发生事件a产生的结果
表示a发生观测事件发生的比例
表示a未发生观测事件发生的比例
那么事件A对Y事件存在因果效应。
如果 则平均因果效应不存在,零假设为真。
平均因果效应不存在不代表不存在个体因果效应。
通常使用E来表示平均因果效应,毕竟期望的标
即
这个式子看下图

是 a发生时Y发生的次数/总数 第二行1的个数/总数 为0.5
是 a不发生时Y发生的次数/总数 第一行1的个数/总数 为0.5
每个个体间差异/总数, 即
total就是总数20,也就是第二行第一列减去第一行第一列,第二行第二列减去第一行第二列, 第二行第三列减去第一行第三列 。。。求和除总数
3 因果效应度量

分别为的风险差、风险比和比值比,这里度量的是人群的因果效应并非个人的因果效应或均值的因果效应。
粘一段
比如,在一大群人中,如果我们进行治疗,一百万 人中会有 1 人得病,如果我们不进行治疗,一百万人中会有 3 人得病。这里的因果性风险比是 3(3/100w除1/100w),但是因果性风险差为 0.000002(3/100w - 1/100w)。这里的因果性风险比(乘法尺度),是用来计算相对于治 疗,不治疗的人患病风险升高的倍数。
4 随机变异性
这点很好理解,由于观测的都是随机时间,所以个体的每次观测结果也是随机的,如中国和越南比赛20场,有可能赢10场也有可能赢5场,中国队能不能赢本身是一个概率。不同的观测样本可能会造成一定偏差。
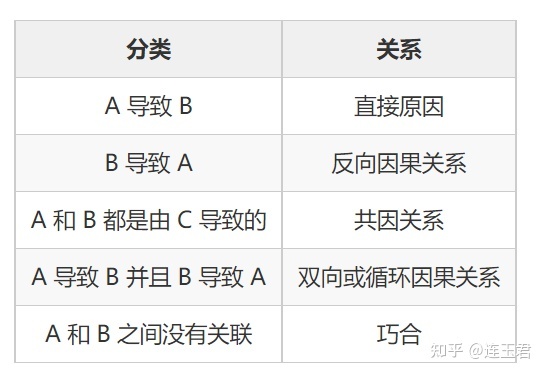
5 因果性与相关性
反事实结局 这个名词简单理解就是 观测事件几乎不可能发生条件相同的情况下,另一个事件发生或不发生两种结果,a事件是否发生在同一条件下只发生一次,而上述观测都是全部发生了。

真实事件只存在不同样本,A是否发生时Y是否也发生。
图中也比较清楚的表示因果推断中因为是反事实结局,每一个随机变量都会产生对应不同结局,而条件概率时通过全集去统计当A发生时Y发生的概率。
(1)当我们比较这 20 个人治疗和不治疗的反事实 结局时,我们没有发现因果效应;(2)当我们比较能观测到的 13 个人治疗和 7 个人不治疗的结 局时,我们发现治疗和结局相关。这个人群(用方块表示)被 分成治疗(白色)和不治疗(灰色)两部分。
这里照搬
因果性的定义需要我们先把这个方块全部涂成白色或者灰色,然后再进行对比。而相关性只 需要我们对比原方块中的白色和灰色两部分。也就是说,因果推断提出的问题是反事实世界究竟是什么样的,比如“如果所有人都接受治疗,死亡风险是多少?”,或者“如果所有人都不接受 治疗,死亡风险是多少?”。与之相比,相关性则只是对现实世界提出问题,比如“在接受治疗 的人群中,死亡风险是多少?”,或者“在未接受治疗的人群中,死亡风险是多少?”

因果性指的是在改变X后Y随之也发生变化,我们称X是Y的因;相关性指在观测到的数据分布中,若果我们观测到了X的分布就可以推断出Y的分布。因此从定义可以得出,相关性是对称的,即若X和Y相关,则Y和X相关;但是因果性是非对称的。相关性不一定说明因果性,但是因果一般会在统计层面导致相关性。
因果关系的存在,必然会伴随着相关性。但是,从因到果还需时间上的先后顺序、以及合理的机制等。因此,相关性只是因果关系的必要不充分条件。
6 条件独立
如 13人接收治疗(A=1) 而7人死亡(Y=1),则即接收治疗的人死亡风险。
条件概率 取值a结局为Y的比例。
当 时治疗A和结果Y是独立或不关联的。写作
![]()
并有:
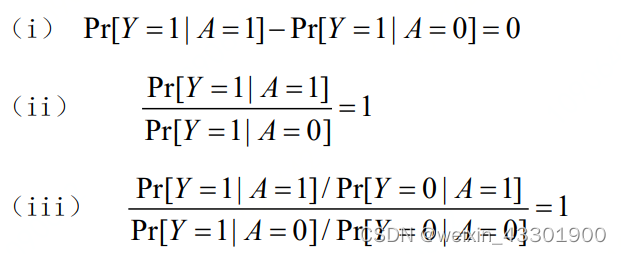
在这个问题中: 快速回忆一下数据,共20个人选择治疗13人7人Y=1,未选择治疗7人3人Y=1。
而 这里如果用均值来看的话E[Y|A=0]=E[Y|A=1],这里这两张图如第5个,图1可以观测到a为1和0时Y都为0,图2只能观测到a为1时的Y为0。第6个也是一样图1能观测到a为1的时候Y为0,a为0的时候Y为1,而图2只能观测到a为1时Y为0。
参考:
因果推断入门(Ⅰ) - 知乎
相关关系和因果关系的区别是什么? - 知乎
这篇关于因果推断笔记1基础符号及表述的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







