【数据结构】--二叉树递归题记

本文主要是介绍【数据结构】--二叉树递归题记，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

最近写了几道关于二叉树的剑指offer题，和小伙伴们分享一下心得。

🌈对称的二叉树

请实现一个函数，用来判断一棵二叉树是不是对称的。如果一棵二叉树和它的镜像一样，那么它是对称的。

思路分析：

对于二叉树的问题来说肯定是用递归进行解决。至于如何解决有待考究，但是

第一步肯定是判断root是不是空。

第二步是进行递归到左右子树进行比较子树的值。这里会遇到两种情况：

若是都为空那就是对称的返回true.
若只有一个节点为空或者对称节点间的val值不等，则返回false，因为这两种情况下，该二叉树不满足对称的要求。

第三步：如果对称节点的值相等，则需要进一步比较左子树的左孩子与右子树的右孩子是否对称，以及左子树的右孩子与右子树的左孩子是否对称，若都对称则返回true，否则返回false。

class Solution {
public:bool isSymmetric(TreeNode* root) {// 如果是空树if(!root)//如果结点不是空就进入判断，但是这个逻辑取反，如果是空就进入判断return true;else//进入子节点继续比较return isSymmetric(root->left, root->right);}// 函数重载，此函数比较二叉树中位置对称的两个节点bool isSymmetric(TreeNode* left, TreeNode* right){// 结束条件1：如果对称两个节点都为空，则返回trueif(!left && !right){return true;}// 结束条件2：如果单独一个节点为空，另一个节点不为空，又或者是对称节点间的val值不等，则返回falseif(!left || !right || left->val != right->val)return false;// 结点不是空并且相等return isSymmetric(left->left, right->right) && isSymmetric(left->right, right->left);      }
};

🌈二叉树的镜像

请完成一个函数，输入一个二叉树，该函数输出它的镜像。

例如输入：

                    4
                   /   \
                 2 7
                / \ / \
              1   3 6   9

镜像输出：

                     4
          /   \
                 7 2
                 / \ / \
               9   6 3   1

解题思路：

第一步：根节点是空
第二步：一直递归直到进到最底层根节点位置。从底层开始交换。
第三步：分别记录下最左边，最右边子树的结点值，然后交换，这样层层交换，最后实现镜像。
class Solution {
public:TreeNode* mirrorTree(TreeNode* root) {if (root == nullptr) {return nullptr;}TreeNode* left = mirrorTree(root->left);TreeNode* right = mirrorTree(root->right);root->left = right;root->right = left;return root;}
};
先在栈中存入4，先递归的是左子树，所以把2存入栈中，继续递归到左子树1，但是1是空节点，返回到根2，然后递归2的右子树3，存入栈中，交换1，3后出栈。返回根节点2。

栈底栈底
4 4
2 2
1 ...
3
...

然后递归2的根节点4的右子树，把7压入栈中。同理压入左右子树6，9

栈底栈底
4 4
2 2
... 7
6
9 ...
交换左右子树后出栈并且返回根节点7。再交换2，7并且出栈。最后把根节点4出栈 .返回根节点4.
栈底栈底
4 4
2 ...
7...

🌈二叉树剪枝

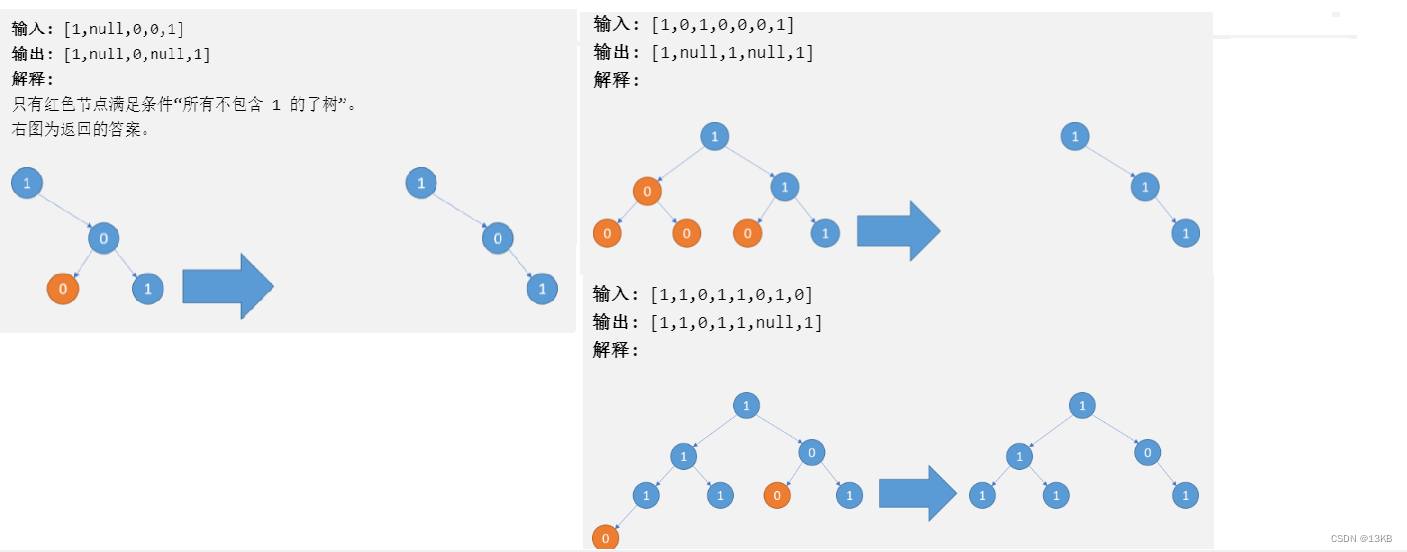
给定一个二叉树根节点 root ，树的每个节点的值要么是 0，要么是 1。请剪除该二叉树中所有节点的值为 0 的子树。

节点 node 的子树为 node 本身，以及所有 node 的后代。

剪枝后的二叉树满足如下要求：

对于每个节点，如果该节点为叶子节点（没有左右子树），且该节点的值为0，则将该节点剪掉。
对于非叶子节点，如果其左子树和右子树都被剪掉了（即为空指针），且该节点的值为0，则将该节点剪掉。

具体实现思路：递归地对每个节点进行处理，首先对其左右子树进行递归，然后判断当前节点是否为叶子节点，如果是则判断其值是否为0，如果是则将该节点剪掉，返回nullptr；如果不是叶子节点，则判断其左右子树是否都为空指针且该节点的值是否为0，如果是则将该节点剪掉，返回nullptr；否则直接返回该节点的指针。

这个最重要的问题就是如何实现把该剪枝的部分置为空？

如果需要被剪枝，则返回nullptr，将当前节点的左子树指针置为nullptr。
class Solution {
public:TreeNode* pruneTree(TreeNode* root) {if (root == nullptr) {return nullptr;}root->left = pruneTree(root->left);//这一句代码的作用是递归调用pruneTree函数来判断当前节点的//左子树是否需要被剪枝，如果需要被剪枝，则返回nullptr，将当前节点的左子树指针置为nullptr，root->right = pruneTree(root->right);if (root->left == nullptr && root->right == nullptr && root->val == 0) {return nullptr;}return root;}
};
你们发现没。这种二叉树的递归问题一般都是从下往上或者从上往下整活。但是从下往上用的比较多虽然效率不高。我们拿第二个举例：

1

/ \

0 1

/ \ / \

0 0 0 1

先把1存入栈中，然后递归左子树把0存入栈，在存入0的左子树，

栈底返回值
1 1
0 nullptr
0 nullptr

0给根返回空并且出栈，然后调用0的右子树，入栈，它的左右子树都是0，返回nullptr.

同第一左根节点0的左右子树都是0，也进行赋值为nullptr并且出栈。然后1的右子树进栈执行同样操作。

栈底栈底
1 1
1 1
0 1