本文主要是介绍算法分析与设计——2.8 半数集问题,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
问题描述:给定一个自然数n,由自然数n开始可以依次产生半数集set(n)中的数如下:
(1)n属于set(n)
(2)在n的左边添加一个自然数,但该数不能超过最近添加的数的一半
(3)按此规则,直到不能添加为止
例如:set(6)={6,16,26,36,126,136}=6
算法设计:对于给定的自然数n,计算set(n)中的元素个数
输入:自然数n
输出:元素个数和元素内容
算法思想:以6为例。按照规则,新加入的数字小于等于6的一半——3。所以6进行一轮,添加了1,2,3三个数字组合为16,26,36。接下来发现只有26和36可以按照规则继续加数字。
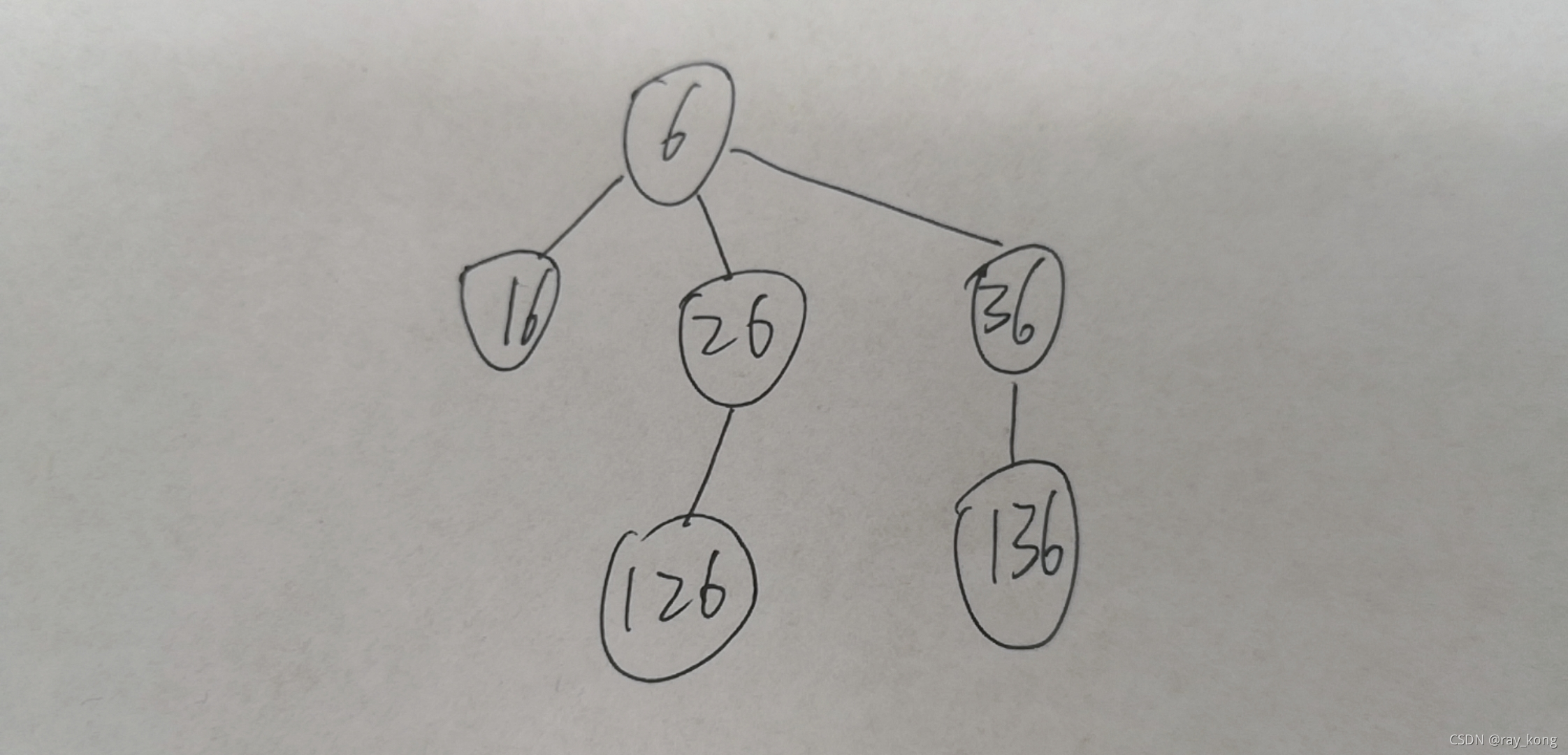
根据规则,对每一个数n最多可以添加n/2个数字且不重复,如果把每一个自然数看作树的节点,那么对一棵树上的节点来说都有n/2个子节点。符合分治策略的使用条件。有如下递归式:
这篇关于算法分析与设计——2.8 半数集问题的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






