分治算法——半数集问题

半数集问题

什么是半数集？
给定一个自然数n，在n的左边加上一个自然数，但该自然数不能超过最近添加的数的一半。
举个例子：若n=6，求6的半数集。
{6，16，26，126，36，136}
6半数集肯定包含他本身；
1不大于的一半 所以16；
2不大于6的一半，26；1又不大于2，所以126；
3不大于6的一半，36；1又不大于3，所以136；

解题思路

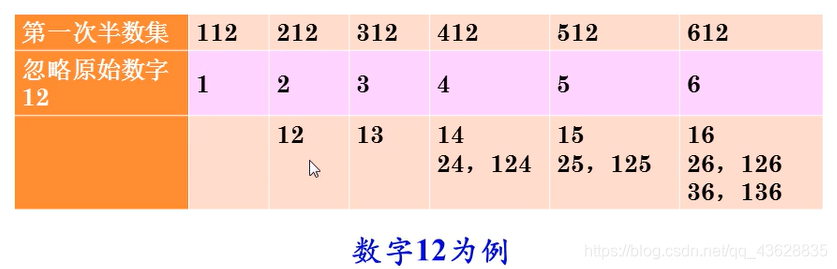
由图可知，12的半数集依赖于1至6的半数集。
1（本身）+1的半数集个数+2的+…+6的半数集个数=12的半数集个数。
而每个子半数集又依赖于它们的子半数集，则可利用递归调用实现算法。
得出一个公式：

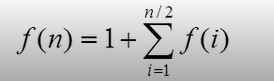
具体实现

int comp(int n){		int ans=1;		//定义变量 初始为1，为该数自身；if(n>1){			//若求1的半数集 则就是1，若大于1 则执行；for(int i=1;i<=n/2;i++)			//循环从1 加到 n/2 半数集ans+=comp(i);}return ans;						//返回半数集个数
}

以上的代码实现有一些重复的计算，例如算12的半数集时已经算过了1-6的半数集，而算6的半数集时算了1-3的半数集，1-3的半数集重复了多次。

//记忆式搜索
int a[100];		//定义一个数组，来存储对应半数集个数
int comp(int n){		int ans=1;		//定义变量 初始为1，为该数自身；if(a[n]>0)return a[n];	//如果a[n]>0，证明n的半数集已经被算过，保存到了数组a[n]里，直接返回；for(int i=1;i<=n/2;i++)			//循环从1 加到 n/2 半数集ans+=comp(i);a[n]=ans;				//如果n的半数集没被算过，现在算过了，保存到a[n]中，返回ans或者a[n]都行。return ans;						//返回半数集个数
}