算法分析_半数集问题

问题描述：
给定一个自然数n，由n开始可以依次产生半数集set(n)中的数如下：
(1) n∈set(n)；
(2) 在n的左边加上一个自然数，但该自然数不能超过最近添加的数的一半；
(3) 按此规则进行处理，直到不能再添加自然数为止。

例如，set(6)={6,16,26,126,36,136}，半数集set(6)中有6个元素。
输入：整数n(0<n<1000)
输出：半数集set(n)中的元素个数。

分析：
首先应该明确什么是半数集，半数集就是给定一个数，在这个数的左边添加新的数字（如6，左边添加新的数字2，就变为26），新添加的数字应该小于或等于这个数的左边第一个数字的一半（如59，则应当小于5/2），所以叫做半数，而由这些数字构成的集合就是半数集。

以6为例，6的半数集求解图示如下：

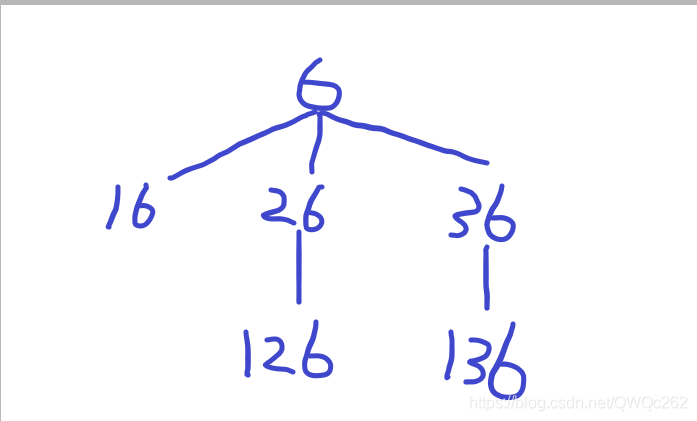
源代码如下（递归与非递归均有）：

package recursion;import java.util.Scanner;public class Half_set {int set(int n) {int sum=1;//该数本身也属于半数集，故初始个数为1if(n<=1)return 1;for(int i=1;i<=n/2;i++) {sum=sum+set(i);}return sum;}int set(int n,int a[]){//优化后，非递归算法int ans = 1;if(a[n]>0) return a[n];for(int i = 1;i<=n/2;i++){ans += set(i);}a[n] = ans;return ans;}public static void main(String[] args) {// TODO 自动生成的方法存根Half_set temple=new Half_set();Scanner scanner=new Scanner(System.in);int a[]=new int[1024];int n=scanner.nextInt();//int sum=temple.set(n);//递归调用int sum=temple.set(n, a);//非递归调用System.out.println(sum);}}