本文主要是介绍LEARNING CURVE PREDICTION WITH BAYESIAN NEURAL NETWORKS 论文详解,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
这篇文章网上找了发现并没有人贴过心得之类的文章,所以就权当翻译了,简单记下阅读过程,如果有误还请私信我,谢谢!
LEARNING CURVE PREDICTION WITH BAYESIAN NEURAL NETWORKS
作者:Aaron Klein, Stefan Falkner, Jost Tobias Springenberg & Frank Hutter
Department of Computer Science
ABSTRACT
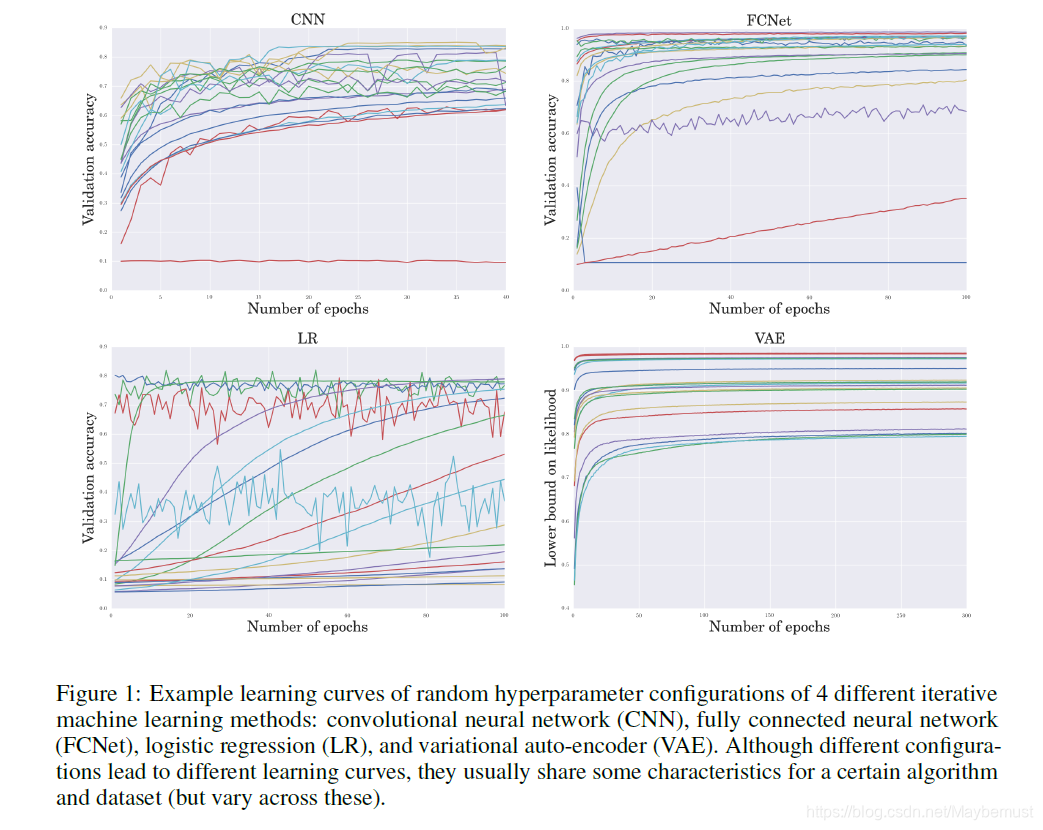
Different neural network architectures, hyperparameters and training protocols lead to different performances as a function of time. Human experts routinely inspect the resulting learning curves to quickly terminate runs with poor hyperparameter settings and thereby considerably speed up manual hyperparameter optimization. The same information can be exploited in automatic hyperparameter optimization by means of a probabilistic model of learning curves across hyperparameter settings. Here, we study the use of Bayesian neural networks for this purpose and improve their performance by a specialized learning curve layer.
不同的网络构架,超参数(可以理解为卷积核等参数)和训练方法造成了了不同的效果。所以专家们希望能够通过训练一个回归模型能够快速中断刁训练结果不好的模型从而加速训练过程。本文研究一个贝叶斯神经网络模型来实现这一目的,并且通过一个专门的学习曲线层来加强原有模型。
1 INTRODUCTION
Deep learning has celebrated many successes, but its performance relies crucially on good hyperparameter settings. Bayesian optimization (e.g, Brochu et al. (2010); Snoek et al. (2012); Shahriari et al. (2016)) is a powerful method for optimizing the hyperparameters of deep neural networks (DNNs). However, its traditional treatment of DNN performance as a black box poses fundamental limitations for large and computationally expensive data sets, for which training a single model can take weeks. Human experts go beyond this blackbox notion in their manual tuning and exploit cheaper signals about which hyperparameter settings work well: they estimate overall performance based on runs using subsets of the data or initial short runs to weed out bad parameter settings; armed with these tricks, human experts can often outperform Bayesian optimization.
深度学习太依赖于超参数的设置。贝叶斯模型可以很好的优化深度神经网络的参数。但是传统的、作为一个黑盒一样使用贝叶斯模型限制了大数据集的表现而且耗时极长。所以专家们就用原始集合的子集或者开始很短一段的训练效果来预测当前超参数情况下训练结果的好坏来快速清除不好的参数。
Recent extensions of Bayesian optimization and multi-armed bandits therefore also drop the limiting blackbox assumption and exploit the performance of short runs (Swersky et al., 2014; Domhan et al., 2015; Li et al., 2017), performance on small subsets of the data (Klein et al., 2017), and performance
on other, related data sets (Swersky et al., 2013; Feurer et al., 2015).
上述是一些分别探索这两类做法的文章和团队。
While traditional solutions for scalable Bayesian optimization include approximate Gaussian process models (e.g., Hutter et al.; Swersky et al. (2014)) and random forests (Hutter et al., 2011), a recent trend is to exploit the flexible model class of neural networks for this purpose (Snoek et al., 2015; Springenberg et al., 2016). In this paper, we study this model class for the prediction of learning curves. Our contributions in this paper are:
传统的贝叶斯优化用的是高斯模型、随机森林算法
本文的探索主要由以下几个方面构成:
- We study how well Bayesian neural networks can fit learning curves for various architectures and hyperparameter settings, and how reliable their uncertainty estimates are.
- Building on the parametric learning curve models of Domhan et al. (2015), we develop a specialized neural network architecture with a learning curve layer that improves learning curve predictions.
- We compare different ways to generate Bayesian neural networks: probabilistic back propagation (Hernández-Lobato and Adams, 2015) and two different stochastic gradient based Markov Chain Monte Carlo (MCMC) methods – stochastic gradient Langevin dynamics (SGLD (Welling and Teh, 2011)) and stochastic gradient Hamiltonian MCMC (SGHMC (Chen et al., 2014)) – for standard Bayesian neural networks and our specialized architecture and show that SGHMC yields better uncertainty estimates.
- We evaluate the predictive quality for both completely new learning curves and for extrapolating partially-observed curves, showing better performance than the parametric function approach by Domhan et al. (2015) at stages were learning curves have not yet converged.
- We extend the recent multi-armed bandit strategy Hyperband (Li et al., 2017) by sampling using our model rather than uniformly at random, thereby enabling it to approach nearoptimal configurations faster than traditional Bayesian optimization.
这几方面分别是:
- 探究了贝叶斯神经网络能在多大限度上预测不同网络结构和参数设置的学习曲线,预估其可靠性。
- 基于Domhan et al.(2015)的成果,在原有网络结构的基础上添加了一个专门的学习曲线层来提高曲线的预测精度。
- 通过多种方式来生成贝叶斯神经网络:概率的反向传播和随机梯度算法。基于的理论原型见上文英文原文。同时也表明SGHMC的模型在不确定性预估上表现最好。
- 评估了完全新建的学习曲线和外推的部分观测的曲线。
- 改良了多臂赌博机模型。通过采样本文的模型而不是完全随机生成。
2 PROBABILISTIC PREDICTION OF LEARNING CURVES
In this section, we describe a general framework to model learning curves of iterative machine learning methods. We first describe the approach by Domhan et al. (2015) which we will dub LCExtrapolation from here on. Afterwards, we discuss a more general joint model across time steps and hyperparameter values that can exploit similarities between hyperparameter configurations and predict for unobserved learning curves. We also study the observation noise of different hyperparameter configurations and show how we can adapt our model to capture this noise.
这一部分描述了迭代机器学习的大体框架。首先是
T. Domhan, J. T. Springenberg, and F. Hutter. Speeding up automatic hyperparameter optimization of deep neural networks by extrapolation of learning curves. In Q. Yang and M. Wooldridge, editors, Proc. of IJCAI’15, 2015.
建立了一个更一般的随时间步和超参数值改变的模型。同时,也研究了不同超参数下的观测噪声以使模型适应捕获这些干扰。
2.1 LEARNING CURVE PREDICTION WITH BASIS FUNCTION
一个直观的模型使使用一组k个不同参数函数\phi来外推学习曲线y。每个参数函数\phi都是关于时间和参数向量的函数并且公国权重线性组合起来。
这一通公式还是自己看吧,我也看不太懂担心误导。
For our experiments, we use the original implementation by Domhan et al. (2015) with one modification: the original code included a term in the likelihood that enforced the prediction at t = T to be strictly greater than the last value of that particular curve. This biases the estimation to never underestimate the accuracy at the asymptote. We found that in some of our benchmarks, this led to instabilities, especially with very noisy learning curves. Removing it cured that problem, and we did not observe any performance degradation on any of the other benchmarks.
The ability to include arbitrary parametric functions makes this model very flexible, and Domhan et al. (2015) used it successfully to terminate evaluations of poorly-performing hyperparameters early for various different architectures of neural networks (thereby speeding up Bayesian optimization by a factor of two). However, the model’s major disadvantage is that it does not use previously evaluated hyperparameters at all and therefore can only make useful predictions after observing a substantial initial fraction of the learning curve.
在本文的实验中,对于原来的模型只有一个修改,强制在t= T时刻的预测值严格大于特定曲线的最后一个值。但是这七大的不稳定性,尤其是对于噪声干扰特别多的学习曲线。
这种包含算术函数的方法让模型更加灵活,而且已经成功发挥作用。但是,这个模型最大的问题是完全不借鉴先前的超参数所以只能在观测到大量的初始训练结果才能预测(我的理解是这种方式不能通过先前的结果预测,而是必须开始训练才能知道结果,比如说我通过先前的训练知道两个每个元素都大于0的向量相加结果每个元素一定大于0,但是却不会借鉴这个结果,而是再计算开始的几个,发现都大于0然后才预测;只是类比形式,不类比其他的,别被误导了 )。
2.2 LEARNING CURVE PREDICTION WITH BAYESIAN NEURAL NETWORKS
In practice, similar hyperparameter configurations often lead to similar learning curves, and modelling
this dependence would allow predicting learning curves for new configurations without the need
to observe their initial performance. Swersky et al. (2014) followed this approach based on an approximate Gaussian process model. Their Freeze-Thaw method showed promising results for finding good hyperparameters of iterative machine learning algorithms using learning curve prediction to allocate most resources for well-performing configurations during the optimization. The method introduces a special covariance function corresponding to exponentially decaying functions to model the learning curves. This results in an analytically tractable model, but using different functions to account for cases where the learning curves do not converge exponentially is not trivial.
在实验中,相似的超参数会导致相似的学习曲线,对它们的独立性建模可是让曲线在不需要观测他们开始一些点训练情况下就可以进行预测。Swersky et al.2014就是跟着这个思路在高斯分布模型的基础上进行研究。他们的Freeze-Thaw方法就展示了在用学习曲线找到迭代机器学习算法的超参数方面的可靠表现。他们分配了绝大多数的资源用于良好表现的参数确定上。这种方法引入了一种特殊的协方差函数,具有指数衰减的函数形式。这是一种容易分析的形式,但是考虑到并没有更好的能收敛的方法所以也可以接受。
同样的,内中过程比较复杂,所以还是自己慢慢看吧。总之,就是希望能够只根据参数就预测模型的好坏,参数x使一种超参数设置,t是时间步长,g是有效准确度衡量函数。基于观测和采样进行确定和修正。
2.3 HETEROSCEDASTIC NOISE OF HYPERPARAMETER CONFIGURATION
上述模型讨论的都是同方差(分布比较均匀吧)的噪声贯穿于超参数设置。这里取了40组全连接层神经网络并且对于每一个都用R=10组伪随机数种子进行评估。数据分布如上图。
Maybe not surprisingly, the noise seems to correlate with the asymptotic performance of a configuration. The fact that the noise between different configurations varies on different orders of magnitudes suggests a heteroscedastic noise model to best describe this behavior. We incorporate this observation by making the noise dependent on the input data to allow to predict different noise levels for different hyperparameters. In principle, one could also model a t dependent noise, but we could not find the same trend across different datasets.
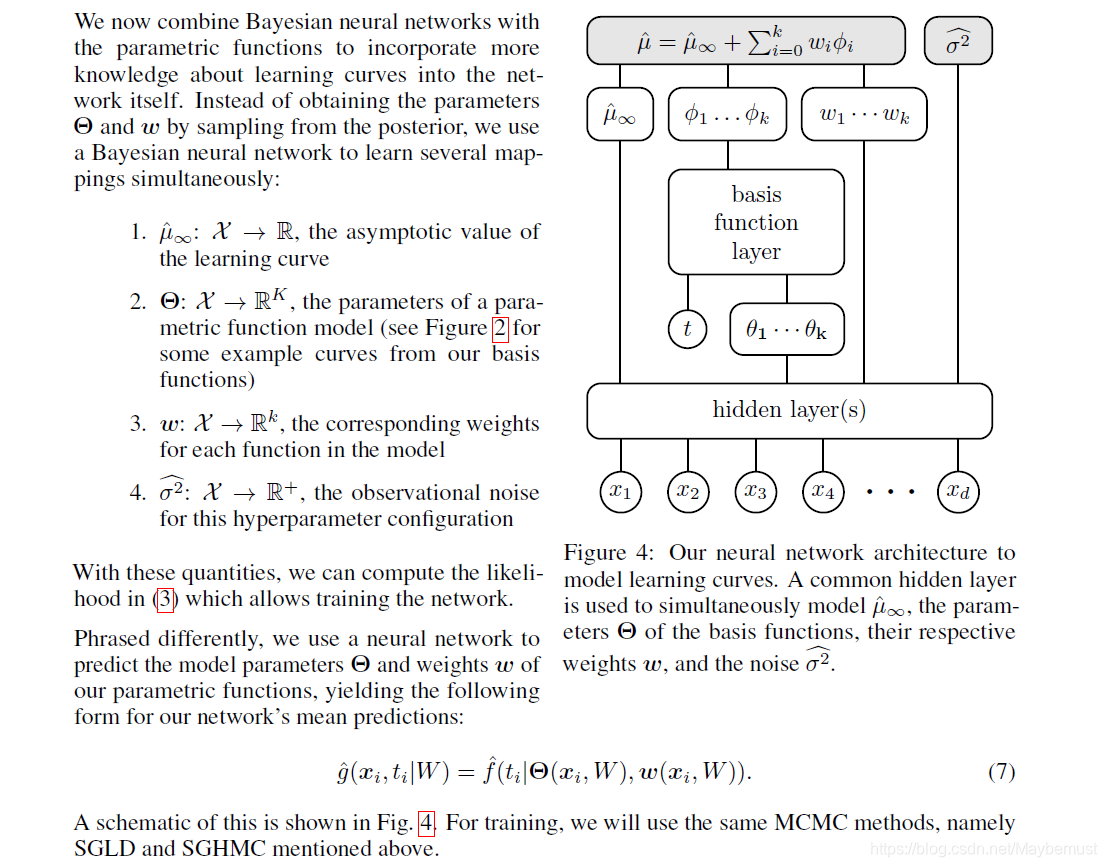
2.4 NEW BASIS FUNCTION LAYER FOR LEARNING CURVE PREDICTION WITH BAYESIAN NEURAL NETWORKS
最后一部分说一下对于新的贝叶斯函数层对于整个网络的影响。
这里将贝叶斯神经网络和参数函数进行结合,取代原来获取参数的方法。架构见上图。
3 EXPERIMENTS
实验部分还是看原文吧,里面有一些处理的具体细节。
这篇关于LEARNING CURVE PREDICTION WITH BAYESIAN NEURAL NETWORKS 论文详解的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!