本文主要是介绍士兵杀敌(二) n 116,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
我理解的还不太到位,这个似乎是对数组的 分块 求和,利用c数组实现a数组的分块分层求和,复杂度降为log2N
南将军手下有N个士兵,分别编号1到N,这些士兵的杀敌数都是已知的。
小工是南将军手下的军师,南将军经常想知道第m号到第n号士兵的总杀敌数,请你帮助小工来回答南将军吧。
南将军的某次询问之后士兵i可能又杀敌q人,之后南将军再询问的时候,需要考虑到新增的杀敌数。
- 输入
- 只有一组测试数据
第一行是两个整数N,M,其中N表示士兵的个数(1<N<1000000),M表示指令的条数。(1<M<100000)
随后的一行是N个整数,ai表示第i号士兵杀敌数目。(0<=ai<=100)
随后的M行每行是一条指令,这条指令包含了一个字符串和两个整数,首先是一个字符串,如果是字符串QUERY则表示南将军进行了查询操作,后面的两个整数m,n,表示查询的起始与终止士兵编号;如果是字符串ADD则后面跟的两个整数I,A(1<=I<=N,1<=A<=100),表示第I个士兵新增杀敌数为A.
输出 - 对于每次查询,输出一个整数R表示第m号士兵到第n号士兵的总杀敌数,每组输出占一行
样例输入
5 6
1 2 3 4 5
QUERY 1 3
ADD 1 2
QUERY 1 3
ADD 2 3
QUERY 1 2
QUERY 1 5样例输出
6
8
8
20
问题提出:已知数组a[],元素个数为n,现在更改a中的元素,要求得新的a数组中i到j区间内的和(1<=i<=j<=n).
思考:对于这个问题,我们可以暴力地来解决,从a[i]一直累加到a[j],最坏的情况下复杂度为O(n),对于m次change&querry,合起来的复杂度为O(m*n),在n或m很大的情况下,这样的复杂度是让人无法忍受的.另外,如果没有元素的变更,我们完全可以存储sum[1,k](k=1,2,……),然后对任意给定的查找区间[i,j],都可以方便的用ans=sum[1,j]-sum[1,i-1],当然这只是没有元素改变的情况下的比较优化的解法.那么对于有元素变更的问题是否有更高效的方法呢?(废话!没有我还写啥?!)可以想一下,每次更改的元素是比较少的,有时候甚至每次只改变一个元素,但是在用暴力方法求区间和的时候,却对区间内所有的元素都累加了一遍,这样其实造成了许多无谓的运算.这时候也许会想到如果能把一些结果存起来会不会减少很多运算?答案是肯定的,但问题是怎么存,存什么?如果存任意区间的话,n比较大的时候不但内存吃不消,而且存储的量太大,不易更改,反而得不偿失;那么也许可以考虑存储特定的一些区间(比如说线段树,其实现在讨论的问题用线段树完全可以解,以后再详细写线段树).那么现在重新回过头来,看下这个问题,我们已经确定了要存储一些特定区间sum的想法,接下来我们要解决的无非是两个问题:1、减少更改元素后对这些区间里的sum值的更改时间.2、减少查找的时间.
好了废话了这么半天,无非是想让自己以及看到的人明白为什么要用树状数组.
接下来正式入题.
首先我们可以借鉴元素不变更问题的优化方法,先得到前i-1项之和and前j项之和,以s[i]表示前i项之和,那么sum[i,j]=s[j]-s[i-1].那么现在的问题已经转化为求前i项之和了.另外,我们已经确定要存储一些特定区间的和,现在就要来揭示这些特定的区间究竟指什么.
在文字说明之前先引入一个非常经典的,在网上找到的树状数组文章里几乎都要出现的一个图片
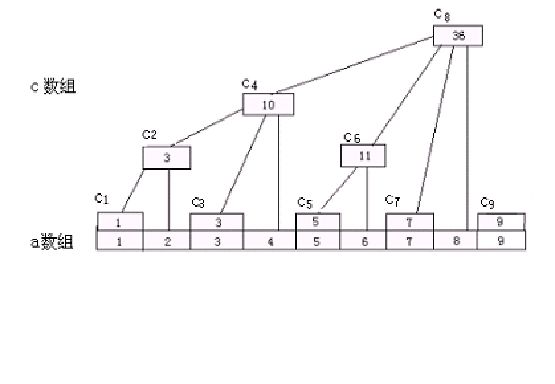
从图中不难发现,c[k]存储的实际上是从k开始向前数k的二进制表示中右边第一个1所代表的数字个元素的和(这么说可能有点拗口,令lowbit为k的二进制表示中右边第一个1所代表的数字,然后c[k]里存的就是从a[k]开始向前数lowbit个元素之和)这么存有什么好处呢?无论是树状数组还是线段树,都用到了分块的思想,而树状数组采用这样的存储结构我想最主要的还是这样方便计算,我们可以用位运算轻松地算出lowbit.分析一下这样做的复杂度:对于更改元素来说,如果第i个元素被修改了,因为我们最终还是要求和,所以可以直接在c数组里面进行相应的更改,如图中的例子,假设更改的元素是a[2],那么它影响到得c数组中的元素只有c[2],c[4],c[8],我们只需一层一层往上修改就可以了,这个过程的最坏的复杂度也不过O(logN);对于查找来说,如查找s[k],只需查找k的二进制表示中1的个数次就能得到最终结果,比如查找s[7],7的二进制表示中有3个1,也就是要查找3次,到底是不是呢,我们来看上图,s[7]=c[7]+c[6]+c[4],可能你还不知道怎么实现这个过程.
还以7为例,二进制为0111,右边第一个1出现在第0位上,也就是说要从a[7]开始向前数1个元素(只有a[7]),即c[7];
然后将这个1舍掉,得到6,二进制表示为0110,右边第一个1出现在第1位上,也就是说要从a[6]开始向前数2个元素(a[6],a[5]),即c[6];
然后舍掉用过的1,得到4,二进制表示为0100,右边第一个1出现在第2位上,也就是说要从a[4]开始向前数4个元素(a[4],a[3],a[2],a[1]),即c[4].
代码实现:
int lowbit(int x)//计算lowbit
{
return x&(-x);
}
void add(int i,int val)//将第i个元素更改为val
{
while(i<=n)
{
c[i]+=val;
i+=lowbit(i);
}
}
int sum(int i)//求前i项和
{
int s=0;
while(i>0)
{
s+=c[i];
i-=lowbit(i);
}
return s;
}
#include<stdio.h>
#include<string.h>int a[1000010], c[100010];
int N, M;int lowbit(int x)
{return x&(-x);
}int sum(int i) //求前i个士兵和
{int s=0;while(i>0){s += c[i];i -= lowbit(i);}return s;
}void change(int x, int m) //第i个士兵又杀敌m
{int i;for(i=x;i<=N;i+=lowbit(i))c[i] += m;
} int main()
{char s[20];memset(c, 0,sizeof(c));scanf("%d%d", &N, &M);int i;for(i=1;i<=N;i++){scanf("%d", &a[i]);change(i, a[i]);}int m, n;while(M--){scanf("%s", s);scanf("%d%d", &m, &n);if(s[0] == 'Q')printf("%d\n", sum(n)-sum(m-1));else if(s[0] == 'A')change(m, n); }return 0;
}
这篇关于士兵杀敌(二) n 116的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




