本文主要是介绍POJ-3304 Segments (判断是否存在一条直线交所以线段),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
问题:
Given n segments in the two dimensional space, write a program, which determines if there exists a line such that after projecting these segments on it, all projected segments have at least one point in common.
Input
Input begins with a number T showing the number of test cases and then, T test cases follow. Each test case begins with a line containing a positive integer n ≤ 100 showing the number of segments. After that, n lines containing four real numbers x1y1 x2 y2 follow, in which (x1, y1) and (x2, y2) are the coordinates of the two endpoints for one of the segments.
Output
For each test case, your program must output "Yes!", if a line with desired property exists and must output "No!" otherwise. You must assume that two floating point numbers a and b are equal if |a - b| < 10-8.
Sample Input
3
2
1.0 2.0 3.0 4.0
4.0 5.0 6.0 7.0
3
0.0 0.0 0.0 1.0
0.0 1.0 0.0 2.0
1.0 1.0 2.0 1.0
3
0.0 0.0 0.0 1.0
0.0 2.0 0.0 3.0
1.0 1.0 2.0 1.0
Sample Output
Yes!
Yes!
No!题目大意:
给你n(n<=100)条线段,问你是否存在一条直线,使得这些线段到这条直线上的投影有一个公共点、
解题思路:
我们可以把题意转化一下。如果存在这么一个公共点,那么从这个公共点向所在直线引一条垂线,这条垂线就会穿过所有线段。那如果我们找到了经过所有线段的直线,然后做垂线就能得到我们要的的那条直线。
题目转化为是否存在一条直线交所有线段。
如果要找这么一条直线,那么我们考虑最极限的情况,即这条直线刚好经过两条线段的端点。注意到n只有100,我们可以暴力枚举,判断是否成立。
判断直线与线段是否相交的方法是:
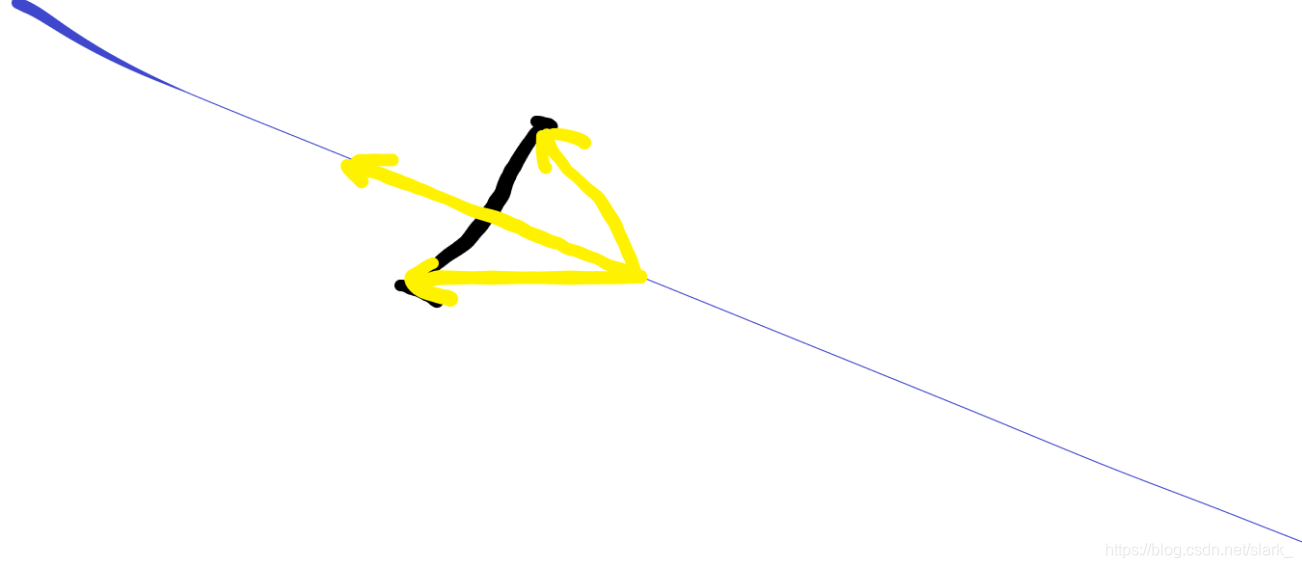
只要判断这条直线向量与从一点到线段两点向量的叉积就行,叉积同号就说明不相交,异号说明相交。
#include<cstring>
#include<algorithm>
#include<cstdio>
#include<queue>
#include<cmath>
#include<iostream>
#include<vector>
#include<map>using namespace std;
const int maxn = 105;
const double eps = 1e-8;struct Point{double x, y;Point(double x = 0.0, double y = 0.0):x(x),y(y){}
};
struct Line{Point a,b;
}l[maxn];Point operator - (Point A, Point B){return Point(A.x-B.x,A.y-B.y);}double Cross(Point A, Point B)
{return A.x*B.y-A.y*B.x;
}
double Dot(Point A,Point B) {return A.x*B.x+A.y*B.y;}
double Length(Point A) {return sqrt(Dot(A,A));}
int dcmp(double x) {if (fabs(x) < eps) return 0;return x < 0? -1: 1;} int isOK(Point A, Point B, Point C, Point D)
{Point v1 = B-A, v2 = C-A, v3 = D-A;double flag1 = Cross(v1,v2);double flag2 = Cross(v1,v3);if(flag1*flag2<=0.000000001) return 1;else return 0;
}
int n;int judge(Point a, Point b)
{if(dcmp(Length(a-b))==0)return 0;for(int i = 1; i <= n; i++){if(!isOK(a,b,l[i].a,l[i].b))return 0;}
// cout <<"## "<< a.x<<" "<< a.y<<" "<<b.x<<" "<<b.y<<endl;return 1;
}int solve()
{for(int i = 1; i <= n; i++){for(int j = 1; j<= n; j++){if(judge(l[i].a,l[j].a)||judge(l[i].b,l[j].a)||judge(l[i].a,l[j].b)||judge(l[i].b,l[j].b))return 1;}}return 0;
}int main()
{int t;scanf("%d", &t);while(t--){scanf("%d", &n);for(int i = 1; i <= n; i++)scanf("%lf%lf%lf%lf", &l[i].a.x, &l[i].a.y, &l[i].b.x, &l[i].b.y);int flag = solve();if(flag||n==1)printf("Yes!\n");elseprintf("No!\n");}return 0;
}
这篇关于POJ-3304 Segments (判断是否存在一条直线交所以线段)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!


