偏置与方差的权衡
高偏置(high bias)与高方差(high variance)的概念在Coursera上Ng的机器学习课程中已经提过,这里不再赘述
预备知识
一致限(the union bound)/Boole不等式(Boole's inequality)
\[P(A_1\cup \cdots \cup A_k)\leq P(A_1)+\cdots+P(A_k)\]
k个事件中,至少一个事件发生的概率,小于等于k个事件发生概率的总和
Hoeffding不等式(Hoeffding inequality)
设\(Z_1,\cdots,Z_m\)是m个独立同分布(independent and identically distributed,iid)的随机变量,每个变量服从相同的伯努利分布\(\mathrm{Bernoulli}(\phi)\),即\(P(Z_i=1)=\phi,P(Z_i=0)=1-\phi\)
令\(\hat \phi=\frac 1 m \sum_{i=1}^m Z_i\)是这些随机变量的平均值。对于常量\(\gamma>0\),有:
\[P(|\phi-\hat\phi|>\gamma)\leq 2\exp(-2\gamma^2m)\]
解释:
根据伯努利分布的性质可知,每个变量\(Z_i\)的期望为\(\phi\),如果现在生成了这m个随机变量(比如做了m次独立重复的抛硬币实验),我们用它们的平均值\(\hat \phi\)作为对每个变量的期望\(\phi\)(或者说伯努利分布的参数\(\phi\))的估计,那么\(\phi,\hat \phi\)之间误差大于\(\gamma\)的概率是小于等于\(2\exp(-2\gamma^2m)\)的,这表明m(实验次数)越大,\(\hat\phi\)越接近真实的\(\phi\)
下面,为了简化说明,考虑二分类问题,标签\(y\in\{0,1\}\),但是下面的内容也可以推广到线性回归、多分类问题等等。
假设现在已有大小为m的训练集\(S=\{(x^{(i)},y^{(i)});i=1,\cdots,m\}\),其中训练样本\((x^{(i)},y^{(i)})\)是独立同分布的,每个样本服从某种概率分布\(\mathcal D\)
对于给定的假设函数\(h\),定义训练误差(经验风险)为:
\[\hat \varepsilon(h)=\frac 1 m \sum_{i=1}^m1\{h(x^{(i)}\neq y^{(i)}\}\]
即,使用假设函数h得到的分类错误的训练样本比例
另外,我们定义泛化误差(generalization error)为:
\[\varepsilon(h)=P_{(x,y)\sim \mathcal D}(h(x)\neq y)\]
即,给出一个新的样本\((x,y)\)服从概率分布D,被错误分类的概率
注意这里有假设:根据训练误差和泛化误差的定义,训练样本和真实样本的概率分布D是完全一样的
考虑用线性决策边界分类,\(h_\theta(x)=1\{\theta^Tx\geq 0\}\),一种通过训练集选取参数\(\hat \theta\)的方法为:
\[\hat\theta=\arg\min_\theta \hat\varepsilon(h_\theta)\]
这种方法就是选取使得训练误差(经验风险)最小的\(\theta\),这被称为经验风险最小化(empirical risk minimization,ERM),逻辑回归算法可以视为ERM的一种近似
在下面的讨论中,我们不关心假设函数\(h\)的具体形式,定义假设函数集(hypothesis class)\(\mathcal H\)是一个学习算法的候选假设函数构成的集合,学习算法的任务是要在\(\mathcal H\)中选取最优(比如经验风险最小)的假设函数\(h_\theta\);例如:对于线性决策边界的逻辑回归问题,\(\mathcal H=\{h_\theta:h_\theta=1\{\theta^Tx\geq 0\},\theta\in \mathbb R ^{n+1}\}\)
如果学习算法在\(\mathcal H\)中选取的是经验风险最小的\(h\),那么最终通过训练集选取的假设函数就是
\[\hat h=\arg \min_{h\in \mathcal H}\hat \varepsilon(h)\]
下面分别就\(\mathcal H\)是有限集和无限集的情况分类讨论:
\(\mathcal H\)是有限集合
若有限集\(\mathcal H=\{h_1,\cdots,h_k\},k\neq +\infty\),那么\(\mathcal H\)是由k个,从输入空间\(\mathcal X\)(input domain)映射到标签集合\(\{0,1\}\)的函数构成的集合。此时ERM会选取其中使得训练误差最小的\(\hat h\)
首先,我们要证明\(\hat \varepsilon(h)\)是对\(\varepsilon(h)\)很好的估计
然后,我们要证明,\(\hat \varepsilon(h)\)的泛化误差是有上界的
对于任意的\(h_i \in \mathcal H\),令训练样本\((x,y)\sim \mathcal D\),然后,然后令\(Z=1\{h_i(x)\neq y\}\)(\(h_i\)是否会把该样本错误分类,会错误分类则取值为1,反之为0),\(Z\)服从某种伯努利分布。类似地,定义\(Z_j=1\{h_i(x^{(j)})\neq y^{(j)}\}\)(\(h_i\)是否会把第j个训练样本错误分类)
则训练集里每个样本是独立同分布的,服从某种概率分布\(\mathcal D\),每个\(Z_j\)也是独立同分布的,服从相同的伯努利分布
泛化误差\(\varepsilon(h)\)是随机变量\(Z\)的期望,而训练误差是通过训练集对泛化误差的近似估计:
\[\hat \varepsilon(h)=\frac 1 m \sum_{j=1}^m Z_j\]
对于常量\(\gamma>0\),由Hoeffding不等式可得
\[P(|\varepsilon(h_i)-\hat \varepsilon(h_i)|>\gamma)\leq 2\exp(-2\gamma^2m)\]
该不等式表明,训练集大小m越大,假设函数\(h_i\)的训练误差与泛化误差高度相似的概率越大,但该不等式只适用于\(h_i\),我们想让它推广到全体假设函数构成的集合\(\mathcal H\),令\(A_i\)为事件\(|\varepsilon(h_i)-\hat \varepsilon(h_i)|>\gamma\),则
\[P(A_i)\leq 2\exp(-2\gamma^2m)\]
根据一致限(Boole不等式)可得
\[P(\exists h\in\mathcal H,|\varepsilon(h_i)-\hat \varepsilon(h_i)|>\gamma)=P(A_1\cup \cdots \cup A_k)\]
\[\leq \sum_{i=1}^k P(A_i)= 2k\exp(-2\gamma^2m)\]
则
\[P(\neg \exists h\in\mathcal H,|\varepsilon(h_i)-\hat \varepsilon(h_i)|>\gamma)=1-P(A_1\cup \cdots \cup A_k)\]
(不存在\(h\)使得\(|\varepsilon(h_i)-\hat \varepsilon(h_i)|>\gamma\),与存在\(h\)使得\(|\varepsilon(h_i)-\hat \varepsilon(h_i)|>\gamma\),是对立事件)
\[\geq 1-2k\exp(-2\gamma^2m)\]
这一不等式是对于全体假设函数构成的集合\(\mathcal H\)而言的,表明训练集大小m越大,任意一个假设函数\(h_i\in\mathcal H\)的训练误差与泛化误差高度相似的概率越大
不存在\(h\)使得\(|\varepsilon(h_i)-\hat \varepsilon(h_i)|>\gamma\),被称为一致收敛(uniform convergence),因为此时对于所有的h存在一个上界\(\gamma\):\(|\varepsilon(h_i)-\hat \varepsilon(h_i)|\leq \gamma\)
已知\(\gamma\),某个\(\delta>0\),\(m\)需要取到多大的时候才能保证
\(P(\neg \exists h\in\mathcal H,|\varepsilon(h_i)-\hat \varepsilon(h_i)|>\gamma)\geq 1-\delta\)(一致收敛的概率\(\geq 1-\delta\))呢?
当一致收敛的概率\(\geq 1-\delta\)时应有:
\[P(\neg \exists h\in\mathcal H,|\varepsilon(h_i)-\hat \varepsilon(h_i)|>\gamma)\geq 1-2k\exp(-2\gamma^2m)\geq 1-\delta\]
\[2k\exp(-2\gamma^2m)\leq \delta\]
\[-2\gamma^2m \leq \log \frac {\delta}{2k}\]
\[m \geq -\frac 1 {2\gamma^2}\ log \frac {\delta}{2k}\]
\[m \geq \frac 1 {2\gamma^2}\ log \frac {2k}{\delta}\]
表明当\(m \geq \frac 1 {2\gamma^2}\ log \frac {2k}{\delta}\),我们至少有\(1-\delta\)的概率保证一致收敛(所有的\(\varepsilon(h_i)\)与\(\hat \varepsilon(h_i)\)之间的误差小于等于\(\gamma\))。达到\(1-\delta\)概率所需的m的大小被称为一个学习算法的样本复杂度(sample complexity)
上面的不等式表明,在给定\(\delta\)时,训练样本数\(m\)是假设函数集的大小\(k\)的对数级别。
类似地,若已知\(m,\delta\),有\(1-\delta\)的概率一致收敛,此时所有的
\[|\varepsilon(h_i)-\hat \varepsilon(h_i)|\leq \sqrt{\frac 1 {2m}\log \frac {2k} \delta}\]
在一致收敛成立的前提下,上界\(\gamma\geq \sqrt{\frac 1 {2m}\log \frac {2k} \delta}\),\(\forall h\in \mathcal H\)有\(|\varepsilon(h)-\hat \varepsilon(h)|\leq \gamma\),这个不等式后面将会用到
定义\(\hat h=\arg \min _{h\in\mathcal H} \hat \varepsilon(h)\)(用训练集选取出的训练误差最小的假设函数),\(h^*=\arg \min _{h\in\mathcal H} \varepsilon(h)\)(真正的泛化误差最小的假设函数),根据上面的不等式有:
\[\varepsilon(\hat h) \leq \hat \varepsilon(\hat h)+\gamma\]
(根据上面的不等式)
\[\leq \hat \varepsilon(h^*)+\gamma\]
(训练集选出的\(\hat h\)的训练误差,比\(h^*\)要小,否则训练过程选出的就不是\(\hat h\)而是\(h^*\)了)
\[\leq \varepsilon(h^*)+2\gamma\]
(再次用到了上面的不等式)
可见\(\hat h\)的泛化误差最多比\(h^*\)的泛化误差多\(2\gamma\),
\[\varepsilon(\hat h)\leq \varepsilon(h^*)+2\gamma=\min _{h\in\mathcal H}\varepsilon(h)+2\gamma\leq (\min _{h\in\mathcal H}\varepsilon(h))+2\sqrt{\frac 1 {2m}\log \frac {2k} \delta}\]
一致收敛至少有\(1-\delta\)的概率成立,此时\(\varepsilon(h)\)最多比\(\varepsilon(h^*)\)多\(2\gamma\)
当我们把假设函数集\(\mathcal H\)扩充为更大范围的\(\mathcal H',\mathcal H\subset \mathcal H'\)时,\(\min _{h\in\mathcal H}\varepsilon(h)\)只可能减小,而由于假设函数集的大小\(k\)增大,这部分代表着偏差(bias)减小;\(2\sqrt{\frac 1 {2m}\log \frac {2k} \delta}\)会增大,这部分代表着方差(variance)增大
推论
已知\(\gamma,\delta,|\mathcal H|=k\),一致收敛的概率至少为\(1-\delta\),此时
\[m \geq \frac 1 {2\gamma^2}\ log \frac {2k}{\delta}=O(\frac 1 {\gamma^2}\ log \frac {k}{\delta})\]
\(\mathcal H\)是无限集合
对于大多数学习算法而言,其参数都是实数,有无限种取值,这意味着\(\mathcal H\)是无限集合。
但在计算机中,实数是以浮点数形式存储的。假设我们用双精度浮点型(64 bit)存储每个实数,则,每个实数的取值有\(2^{64}\)种情况;如果参数是由\(d\)个实数组成的,则参数的取值有\(2^{64d}\)种情况,换言之,\(\mathcal H\)还是有限集合,大小为\(2^{64d}\)
根据上一节最后的推论,已知\(\gamma,\delta\),\(|\mathcal H|=2^{64d}\),一致收敛的概率至少为\(1-\delta\),有:
\[m \geq O(\frac 1 {\gamma^2}\ log \frac {2^{64d}}{\delta})=O(\frac d {\gamma^2}\ log \frac {1}{\delta})=O_{\gamma,\delta}(d)\]
(在固定\(\gamma,\delta\)不变时,m与d是线性关系,m是d的常数倍,该常数由\(\gamma,\delta\)决定)
这表明训练集大小m最多与d成线性关系。由于之前假设每个参数都是双精度浮点数,这个结论不能完全令人满意,但是大致是正确的。
要推导出更令人满意的结果,就要引出VC维理论了。
VC维(Vapnik-Chervonenkis dimension)理论
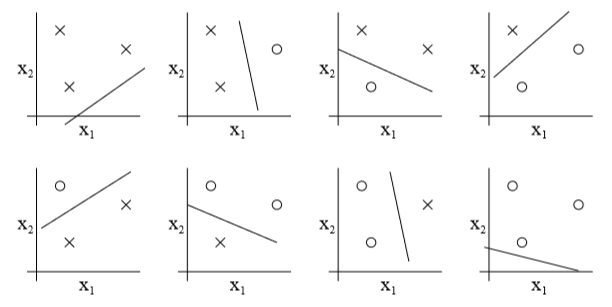
给定d个输入样本\(S=\{x^{(1)},\cdots,x^{(d)}\},x^{(i)}\in \mathcal X\)(这些样本与训练样本毫无关系),如果对这些样本任意给出真实标签\(\{y^{(1)},\cdots,y^{(d)}\}\),总存在\(h\in \mathcal H\),使得\(\forall i=1,\cdots,d,h(x^{(i)})=y^{(i)}\)(h能对S中所有样本都正确分类),则称\(\mathcal H\)的VC维\(\mathrm{VC}(\mathcal H)\geq d\),如果d为无穷大时\(\mathcal H\)也满足上述条件,则\(\mathrm{VC}(\mathcal H)=\infty\)
注意:只要存在某一个大小为d的集合S,能够使得\(\mathcal H\)满足上述条件,就可以说\(\mathrm{VC}(\mathcal H)\geq d\)
例如对于上图这个集合S,\(\mathcal H\)是全体线性分类器构成的集合,对于全部8种标签情况,都能从中找到一个h,使得所有样本都被正确分类:
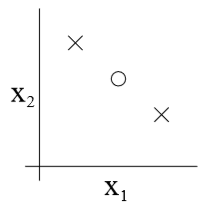
但是,另外取一个如下图所示的,大小为3的集合S,就找不到一个h能够使得所有样本被正确分类
下面不加证明地给出一个重要定理及其推论:
定理: 对于给定的假设函数集合\(\mathcal H\),令\(d=\mathrm{VC}(\mathcal H)\),则至少有\(1-\delta\)的概率,\(\forall h\in\mathcal H\),下面的不等式成立:
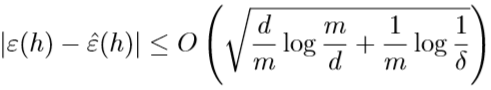
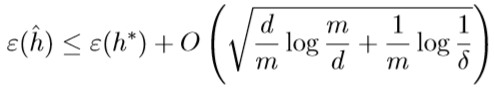
该定理表明,若假设函数集合\(\mathcal H\)是有限VC维的,那么只要m足够大,就能找到上界\(\gamma\),实现一致收敛
推论: 要想至少有\(1-\delta\)的概率实现一致收敛,并找到上界\(\gamma\),从而\(\forall h\in \mathcal H\),有\(|\varepsilon(h)-\hat \varepsilon(h)|\leq \gamma\),\(\varepsilon(\hat h) \leq \varepsilon(h^*)+2\gamma\),则训练集大小\(m=O_{\gamma,\sigma}(d)\)
推论表明,在给定\(\mathcal H\)的前提下,学习算法要想得到好的结果,所需的训练集大小\(m\)是\(O(\mathrm {VC}(\mathcal H))\)级别的