电子科技大学——知识表示与推理（包含prolog运行逻辑说明部分）

prolog语言的运行逻辑说明
主要对于郑旭老师上课提到的重难点以及考试的重点做学习回顾

考试重点内容

• 使用贝叶斯网络做后验概率计算
• 不确定性推理
• prolog语言
• 使用递归分析法做prolog递归分析
• 语义网络
• 一阶逻辑推理

使用贝叶斯网络做后验概率计算

仍以所示的贝叶斯网络为例，假设目前观察到的一个事件s = { c, e }，求在该事件的前提下碰见难题的概率P( D | c, e )是多少？

按照精确推理算法，该询问可表示为：

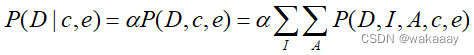
其中，α是归一化常数，D取d和﹁d，应用贝叶斯网络的概率分布公式：
$$P(x1,x2,...,xn)={\Pi }^n(P(x_i|par(X_i)))$$
当D取值d时，有

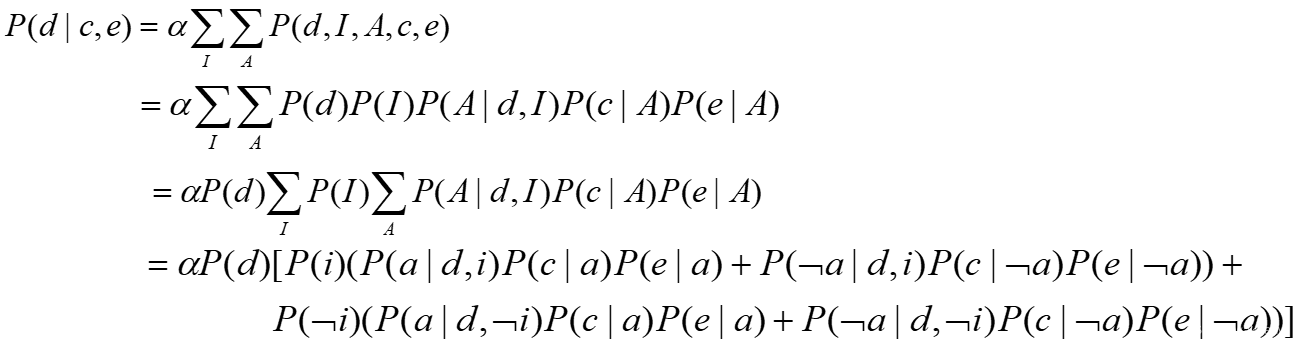
=α×0.15×[0.05×(0.8×0.9×0.9 + 0.2×0.1×0.1)+

​ 0.95×(0.4×0.9×0.9 + 0.6×0.1×0.1)]

​ =α×0.15×[0.05×0.65+0.95×0.33] =α×0.15×0.346

​ =α×0.0519

不确定性推理

当有多条知识支持同一个结论，且这些知识的前提相互独立，结论的可信度又不相同时，可利用不确定性的合成算法求出结论的综合可信度。

设有知识：
IF E1 THEN H (CF(H, E1))
IF E2 THEN H (CF(H, E2))

则结论H 的综合可信度可分以下两步计算：

(1) 分别对每条知识求出其CF(H)。即
​ CF1(H)=CF(H, E1) ×max{0, CF(E1)}
​ CF2(H)=CF(H, E2) ×max{0, CF(E2)}

(2) 用如下公式求E1与E2对H的综合可信度

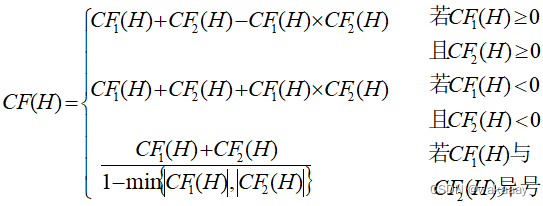
例题1.
设有如下一组知识：
r1：IF E1 THEN H (0.9)
r2：IF E2 THEN H (0.6)
r3：IF E3 THEN H (-0.5)
r4：IF E4 AND ( E5 OR E6) THEN E1 (0.8)
已知：CF(E2)=0.8，CF(E3)=0.6，CF(E4)=0.5，CF(E5)=0.6, CF(E6)=0.8
求：CF(H)=?

解：由r4得到：

CF(E1)=0.8×max{0, CF(E4 AND (E5 OR E6))}

​ = 0.8×max{0, min{CF(E4), CF(E5 OR E6)}}

​ =0.8×max{0, min{CF(E4), max{CF(E5), CF(E6)}}}

​ =0.8×max{0, min{CF(E4), max{0.6, 0.8}}}

​ =0.8×max{0, min{0.5, 0.8}}

​ =0.8×max{0, 0.5} = 0.4
由r1得到：CF1(H)=CF(H, E1)×max{0, CF(E1)}

​ 　　　　　 =0.9×max{0, 0.4} = 0.36

由r2得到：CF2(H)=CF(H, E2)×max{0, CF(E2)}

​ 　　　　　=0.6×max{0, 0.8} = 0.48

由r3得到：CF3(H)=CF(H, E3)×max{0, CF(E3)}

​ 　　　　　 =-0.5×max{0, 0.6} = -0.3

根据结论不精确性的合成算法，CF1(H)和CF2(H)同号，有：

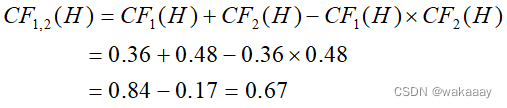
CF_1,2(H)和CF3(H)异号，有：

即综合可信度为CF(H)=0.53

prolog语法（重点——但考试内容一般不会超过五行）

这里我还是放几个供大家做理解哈，基本能够代表考试的一般难度

1. Write a 3-place predicate combine1 which takes three lists as arguments and
   combines the elements of the first two lists into the third as follows:
   ?- combine1([a,b,c],[1,2,3],X).
   X = [a,1,b,2,c,3]
   ?- combine1([foo,bar,yip,yup],[glub,glab,glib,glob],Result).
   Result = [foo,glub,bar,glab,yip,glib,yup,glob]

combine1([],[],[]).
combine1([H31|T1],[H32|T2],[H31,H32|T3]):- combine1(T1,T2,T3).

2. Now write a 3-place predicate combine2 which takes three lists as arguments
   and combines the elements of the first two lists into the third as follows:
   ?- combine2([a,b,c],[1,2,3],X).
   X = [[a,1],[b,2],[c,3]]
   ?- combine2([foo,bar,yip,yup],[glub,glab,glib,glob],Result).
   Result = [[foo,glub],[bar,glab],[yip,glib],[yup,glob]]

combine2([],[],[]).
combine2([H31|T1],[H32|T2],[[H31,H32]|T3]):- combine2(T1,T2,T3).

3. Finally, write a 3-place predicate combine3 which takes three lists as arguments
   and combines the elements of the first two lists into the third as follows:
   ?- combine3([a,b,c],[1,2,3],X).
   X = [join(a,1),join(b,2),join(c,3)]
   ?- combine3([foo,bar,yip,yup],[glub,glab,glib,glob],R).
   R = [join(foo,glub),join(bar,glab),join(yip,glib),join(yup,glob)]

combine3([],[],[]).
combine3([H31|T1],[H32|T2],[join(H31,H32)|T3]):- combine3(T1,T2,T3).

4. Write a predicate addone2/ whose first argument is a list of integers, and whose second argument is the list of integers obtained by adding 1 to each integer in the first list. For example, the query addone([1,2,7,2],X). should give X = [2,3,8,3].

addone([],[]).
addone([H1|T1], [H2|T2]) :-is(H2,+(H1,1)),addone(T1,T2).

这个题基本上考试是不会考的。。。太难了👇

5. Write a Prolog program to implement the predicate frequencies(L,M), which takes as input a list L and returns a list of pairs [x,n], where x is an element of L and n is the number of times x appears in L. Here are some sample runs in SWI Prolog:
   ?- frequencies([a,b,a,c,a,c,d,a],L).
   L = [[a, 4], [b, 1], [c, 2], [d, 1]]
   Yes
   ?- frequencies([],L).
   L = []
   Yes

frequencies([],[]).
frequencies([H|Y],L) :-frequencies(Y,L1),check(H,L1,L).check(H,[],[[H,1]]).
check(H,[[Y,K]|L],[[Y,K1]|L]):- H = Y, K1 is K +1.
check(H,[[Y,K]|L],[[Y,K]|M]) :-H \== Y,check(H,L,M).
check(H,[[H,K]],[[H,K1]]):- K1 is K +1.
check(H,[[Y,K]],[[Y,K]|[H,1]]) :-H \== Y.

对prolog 语言做递归推理分析（网上很难找到，需要自己做充分的理解）

主要思想：跟着prolog的语句逻辑，先向下进行分析，对于每一次提出的数据，将其加入栈内，直到满足所给的终止条件，开始倒着进行——从语句右边到左边，同时将数据栈中的元素加入进来，最终得到推理结果。

qsort([],[]).qsort([H|T],S) :- 
​	qsplit(H,T,A,B),
​	qsort(A,A1),
​	qsort(B,B1),append(A1,[H|B1],S).# 补充
qsplit(H,[A|X],[A|Y],Z) :- A =< H, qsplit(H,X,Y,Z).
qsplit(H,[A|X],Y,[A|Z]) :- A > H, qsplit(H,X,Y,Z).
qsplit(_,[],[],[]).

我们以以上代码为例，假设对qsort（[3,2,1],X）做递归分析，如下：

1. 寻找递归分析语句（哪些语句讲列表中元素做了取出处理）：

qsort([H|T],S) :-         ------------------------------------Ⅰ
​	qsplit(H,T,A,B),      
​	qsort(A,A1),
​	qsort(B,B1),append(A1,[H|B1],S).qsplit(H,[A|X],[A|Y],Z) :- A =< H, qsplit(H,X,Y,Z). ----------Ⅱ（①）
qsplit(H,[A|X],Y,[A|Z]) :- A > H, qsplit(H,X,Y,Z).------------Ⅱ（②）

ps：这里类似于一个选择语句，Ⅱ中只会有①或②执行

2. 找到递归终止条件语句：

qsort([],[]). ------------------------------------------------- （a）
qsplit(_,[],[],[]).-------------------------------------------- （b）

3. 利用分析栈做递归分析（这里是qsort（[1，3，2],X）做递归分析，请大家尝试使用别的例子做分析）——这个例子本身就比较复杂，只需要明白其思想，因为全部过程都是由计算机内部执行的靠人来分析，可能会忘记每个变量的值，也会出错考试不会有这么复杂的题，一般不会递归嵌套递归，请放心
   
   就如大家所见，此图并没有作完，但是相信大家已经理解了下推递归分析的精髓orz
4. 考试的时候不可能需要大家画出这样的图，只需要对于每个重要步骤的结果，做不动图了手写一个（虽然不一定是最标准的），请大家海涵，我们还是以上述内容为例子：
   
   再次说明一下，这个已经很复杂很复杂了，考试一般不会考这么难，希望能够帮助大家理解prolog的递归运行逻辑。

语义网络——主要理解蕴含关系

在蕴含关系中，有两条指向蕴含节点的弧，一条代表前提条件，标记为ANTE；另一条代表结论，标记为CONSE。

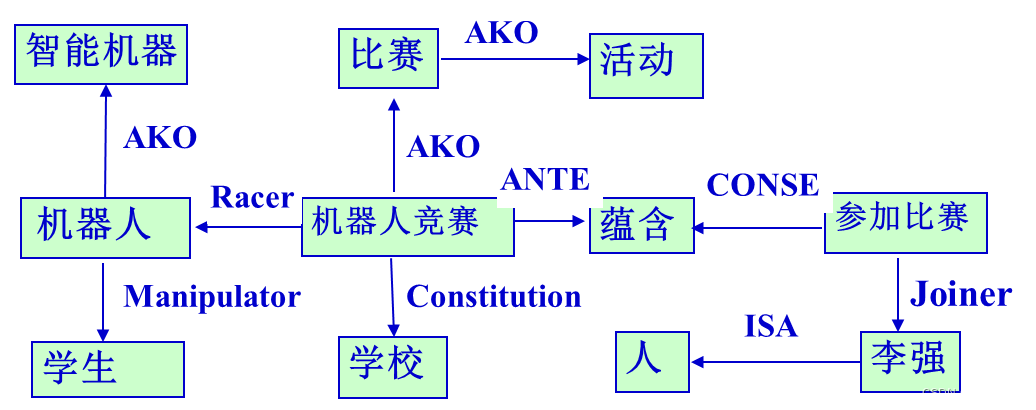
1. 用语义网络表示如下知识：“如果学校组织大学生机器人竞赛活动，那么李强就参加比赛”

该蕴含关系的语义网络如下图。其中，在前提条件中，机器人竞赛的组织者是学校，参赛对象是学生操纵的机器人，而机器人只不过是一种智能机器。

一阶逻辑推导（不打算再这里细说了）