阿亮的算法之路——5. 最长回文子串

本文主要是介绍阿亮的算法之路——5. 最长回文子串，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

题目详情

题目详情
题目链接：https://leetcode-cn.com/problems/longest-palindromic-substring/

初次完成

老规矩，确保自己的第一思路能先完成功能。反正是各种运行调试，有问题就debug

    public String longestPalindrome(String s){String maxSubstr = "";int in;a:for (int i = 0; i < s.length(); i++){String s1 = s.substring(i);char ch = s.charAt(i);b:while ((in = s1.lastIndexOf(ch)) != -1){s1 = s1.substring(0,in+1);for (int n = 0; n < s1.length()/2; n++){if (s1.charAt(n) != s1.charAt(s1.length()-n-1)){s1 = s1.substring(0,s1.length()-1);continue b;}}maxSubstr = maxSubstr.length()>s1.length()?maxSubstr:s1;continue a;}}return maxSubstr;}

感觉能想到的都是最笨的办法，完全没有什么利用算法的思想，幸好没给我说什么超时，不过这效率是真的低
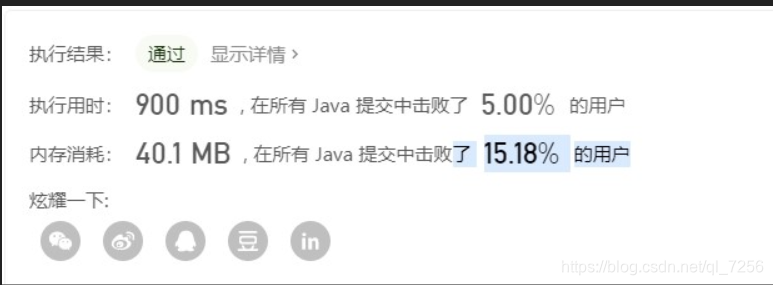第一轮提交思路就是：先定义一个最长的回文串为空字符，从头遍历这个字符串，每个字符，都从后面去找和它相同的字符，如果找到了相同的字符，再往中间判断是否为回文串，是就比较更新最长回文串，不是就再找下一个相同的字符……处理好各种边界条件就OK。

首次优化

关于优化，我首先想到的就是，我第一次提交成功的代码里面，每层循环里使用了很多的字符串截取操作，每遍历一个字符，下一次遍历我都将它截取为一个新的字符串。我觉得字符串的截取，应该挺浪费时间和空间的，所以我决定用StringBuilder来替换有字符串截取的地方。
将能替换的地方都替换为StringBuilder之后(有的地方无法替换)，第二轮代码出来了：

    public String longestPalindrome(String s){StringBuilder st = new StringBuilder("");int in;a:for (int i = 0; i < s.length(); i++){String s1 = s.substring(i);char ch = s.charAt(i);b:while ((in = s1.lastIndexOf(ch)) != -1){s1 = s1.substring(0,in+1);int length = s1.length();for (int n = 0; n < length/2; n++){if (s1.charAt(n) != s1.charAt(length-n-1)){s1 = s1.substring(0,length-1);continue b;}}st = st.length()>s1.length()?st:new StringBuilder(s1);continue a;}}return st.toString();}

然而效果并没很理想：
第二轮提交效率方面有点提升，内存方面还是和原理差不多，我不是将String原生的截取方法换成了StringBuilder吗？按道理内存方面应该会更优秀一些的，这是为什么呢？难道是因为多次创建StringBuilder对象的原因？

再次优化

这次我就在想：我为什么要进行字符串截取操作呢？这些所有的东西，不都可以用字符串的下标来完成吗？只需要最后在返回最长回文子串的时候截取一次不就行了吗？
又开始改了，主要思路不变，只不过全都改成了对字符串索引进行操作

    public String longestPalindrome(String s){int l;if (s == null || (l =s.length()) < 1) return "";int  a = 0,b = 0,c;a:for (int i = 0; i < l; i++){int e = l-1;char f = s.charAt(i);b:while ((c = s.lastIndexOf(f,e)) != -1 && c != i){e = c-1;for (int n = i,m=0; m < (c-i)/2; n++,m++){if (s.charAt(n+1) != s.charAt(c-1-m)){ continue b; }}if (b - a < c - i){ a = i;b = c; }continue a;}}return s.substring(a,b+1);}

这次有那么一丢丢的进步，不过总体来说还是不是很理想
第三次提交
我觉得这已经是我这个思路的极限了，想要再提升，就应该从优化思路考虑了。

大佬思路：

这题的解法，大致有四种：暴力算法、动态规划、中心扩散、Manacher 算法。
我上面的应该就是暴力算法了，思路清晰，好理解，但是缺点就是效率比较低。
动态规划和中心扩散，作为面试者，一定要掌握。至于Manacher 算法，当扩宽视野就好，鉴于目前的水平，也就不拓宽了。就动态规划和中心扩散吃透就好。

动态规划

没系统的学过这个算法，有点烧脑，借大佬的一张图：
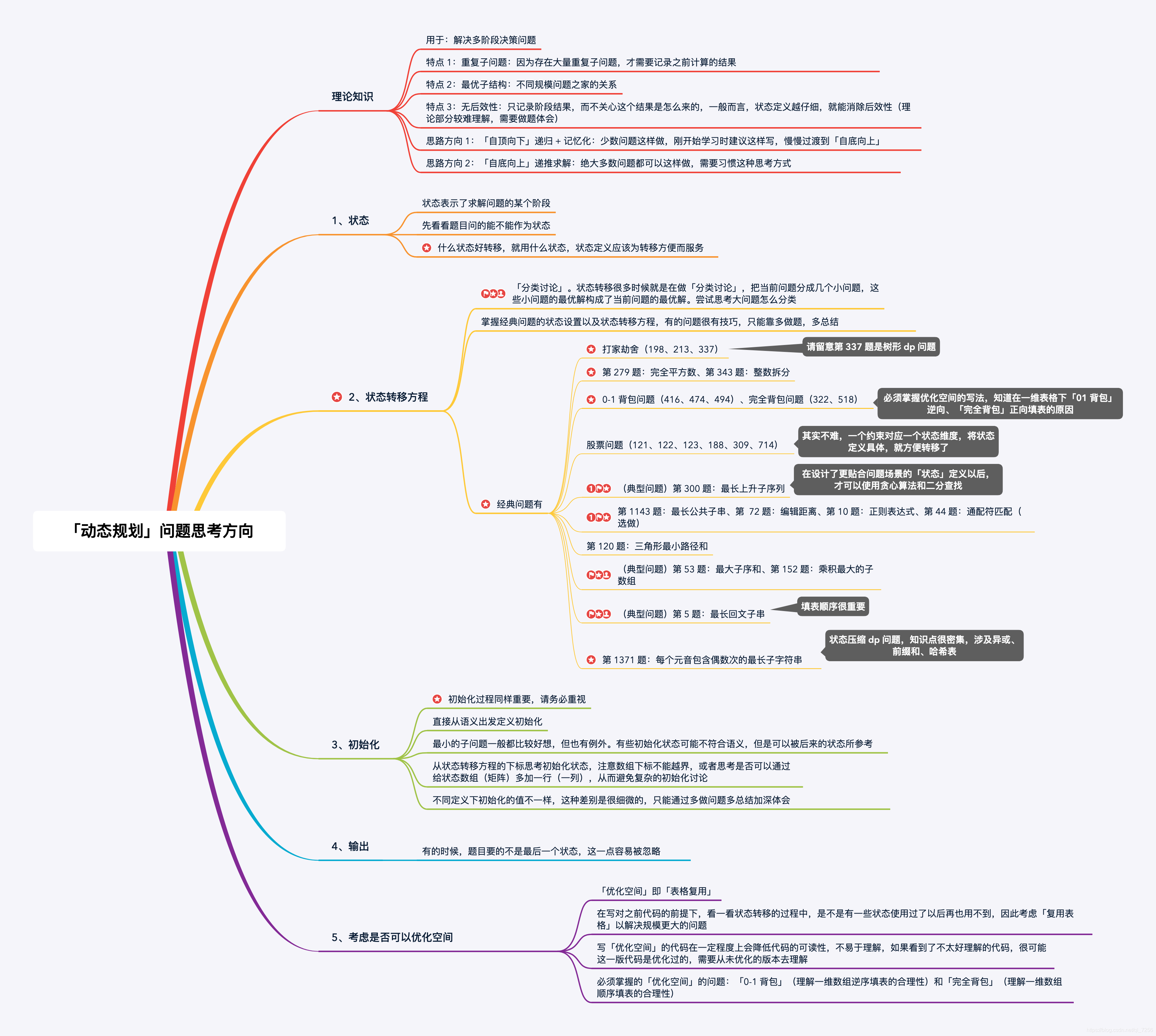动态规划思路主要思路就是：后一个情况的状态是由前面某个情况的状态确定的。具体的细节可以去看这位大佬写的题解：大佬题解，上面这张图片就是在那里保存的。
看了大佬的思路和代码，我自己再写了一遍：

    public String longestPalindrome(String s){//特判int length;if (s == null || (length = s.length()) < 2){ return s; }int start = 0;int end = 0;boolean[][] dp = new boolean[length][length];char[] chars = s.toCharArray();//对角线肯定为truefor (int i = 0; i < length; i++){ dp[i][i] = true; }for (int j = 1; j < length; j++){for (int i = 0; i < j; i++){if (chars[i] == chars[j] ){if (j- i < 3) { dp[i][j] = true; }else{ dp[i][j] = dp[i+1][j-1]; }}if (dp[i][j] && (j-i) > (end-start) ){start = i;end = j;}}}return s.substring(start,end+1);}