本文主要是介绍计算机组成原理-进位计数制(进制表示 进制转换 真值和机器树),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
文章目录
- 现代计算机的结构
- 总览
- 最古老的计数方法
- 十进制计数法
- 推广:r进制计数法
- 任意进制->十进制
- 二进制<--->八进制,十六进制
- 各种进制常见的书写方式
- 十进制->任意进制
- 整数部分
- 小数部分
- 十进制->二进制(拼凑法)
- 真值和机器数
- 小结
- 中国古代的二进制系统
现代计算机的结构

总览
最古老的计数方法
一条竖线对应一个苹果,但数量太多竖线太多画不下
后来用横线表示5,所画的线可以少些
表示数字越大,符号表示越繁琐

十进制计数法

推广:r进制计数法
符号指的是0,1,2,3……这些
注意
二进制1.1+0.1=10.0
八进制5.4+0.4=6.0
十六进制5.8+0.8=6.0
r进制的数对应的小数部分也要记得逢r进1
注意基数是个数

任意进制->十进制
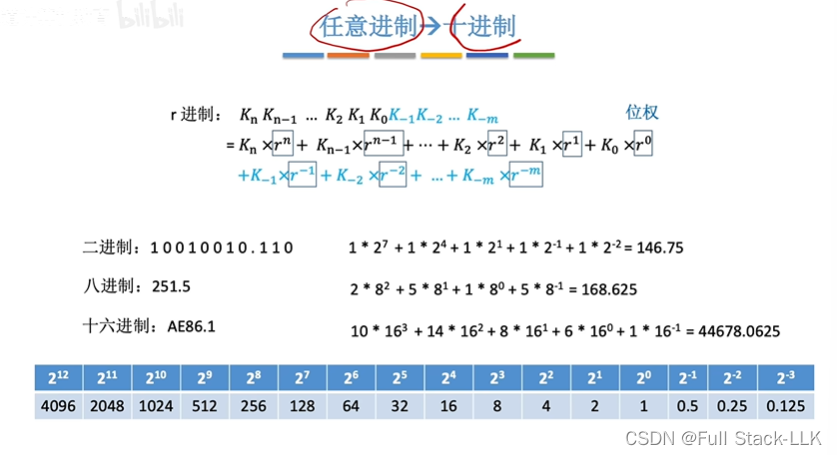
二进制<—>八进制,十六进制
二进制转八进制和十六进制
小数部分位不够往后补0,整数部分位不够往前补0
补到能够取对应位数的个数即可,转换依旧是从取的位数部分右边为低位,左边是高位,然后转换为对应的进制的数值

各种进制常见的书写方式
B:binary

十进制->任意进制
十进制的整数部分对应转换后的进制的整数部分
十进制的小数部分对应转换后的进制的小数部分
这样十进制和转换后进制值的计算出的大小不会变
整数部分

小数部分

十进制->二进制(拼凑法)
找该数等于二进制的那些位的权值的和(或者2的多少次方的和)
转换为二进制后,再转化为八进制和十六进制更方便

真值和机器数

小结
注意补位和小数可能无法用其他进制精确表示
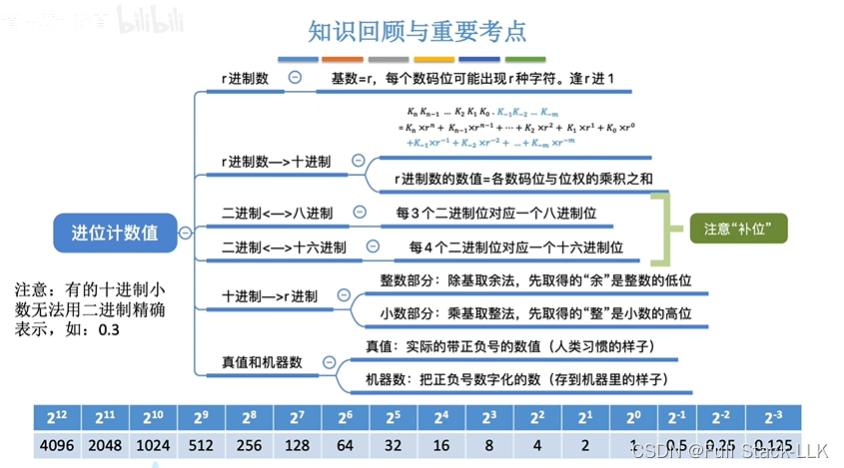
中国古代的二进制系统
太极树的分支对应0和1
这篇关于计算机组成原理-进位计数制(进制表示 进制转换 真值和机器树)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





