本文主要是介绍算法训练day60|单调栈part0,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
参考:代码随想录
84.柱状图中最大的矩形
要求当前柱形的左右两边第一个比他小的位置

对于高度为5的柱子(index为2) mid
他的左边第一个比他小的柱子为1,index为1 left
他的右边第一个比他小的柱子高度为2,index为4 right
对5来说,(left,right)范围内(不包括left,right)都是比5高的柱,所以对5的体积可以是5(h[mid])*(right-left-1)
双指针解法
题要记录记录每个柱子 左边第一个小于该柱子的下标,而不是左边第一个小于该柱子的高度
所以需要循环查找,也就是下面在寻找的过程中使用了while
class Solution {
public:int largestRectangleArea(vector<int>& heights) {vector<int> minLeftIndex(heights.size());vector<int> minRightIndex(heights.size());int size = heights.size();// 记录每个柱子 左边第一个小于该柱子的下标minLeftIndex[0] = -1; // 注意这里初始化,防止下面while死循环for (int i = 1; i < size; i++) {int t = i - 1;// 这里不是用if,而是不断向左寻找的过程while (t >= 0 && heights[t] >= heights[i]) t = minLeftIndex[t];minLeftIndex[i] = t;}// 记录每个柱子 右边第一个小于该柱子的下标minRightIndex[size - 1] = size; // 注意这里初始化,防止下面while死循环for (int i = size - 2; i >= 0; i--) {int t = i + 1;// 这里不是用if,而是不断向右寻找的过程while (t < size && heights[t] >= heights[i]) t = minRightIndex[t];minRightIndex[i] = t;}// 求和int result = 0;for (int i = 0; i < size; i++) {int sum = heights[i] * (minRightIndex[i] - minLeftIndex[i] - 1);result = max(sum, result);}return result;}
};单调栈
但是为了能够计算所有情况,我们需要在首尾都加一个0
本题是要找每个柱子左右两边第一个小于该柱子的柱子,所以从栈头(元素从栈头弹出)到栈底的顺序应该是从大到小的顺序
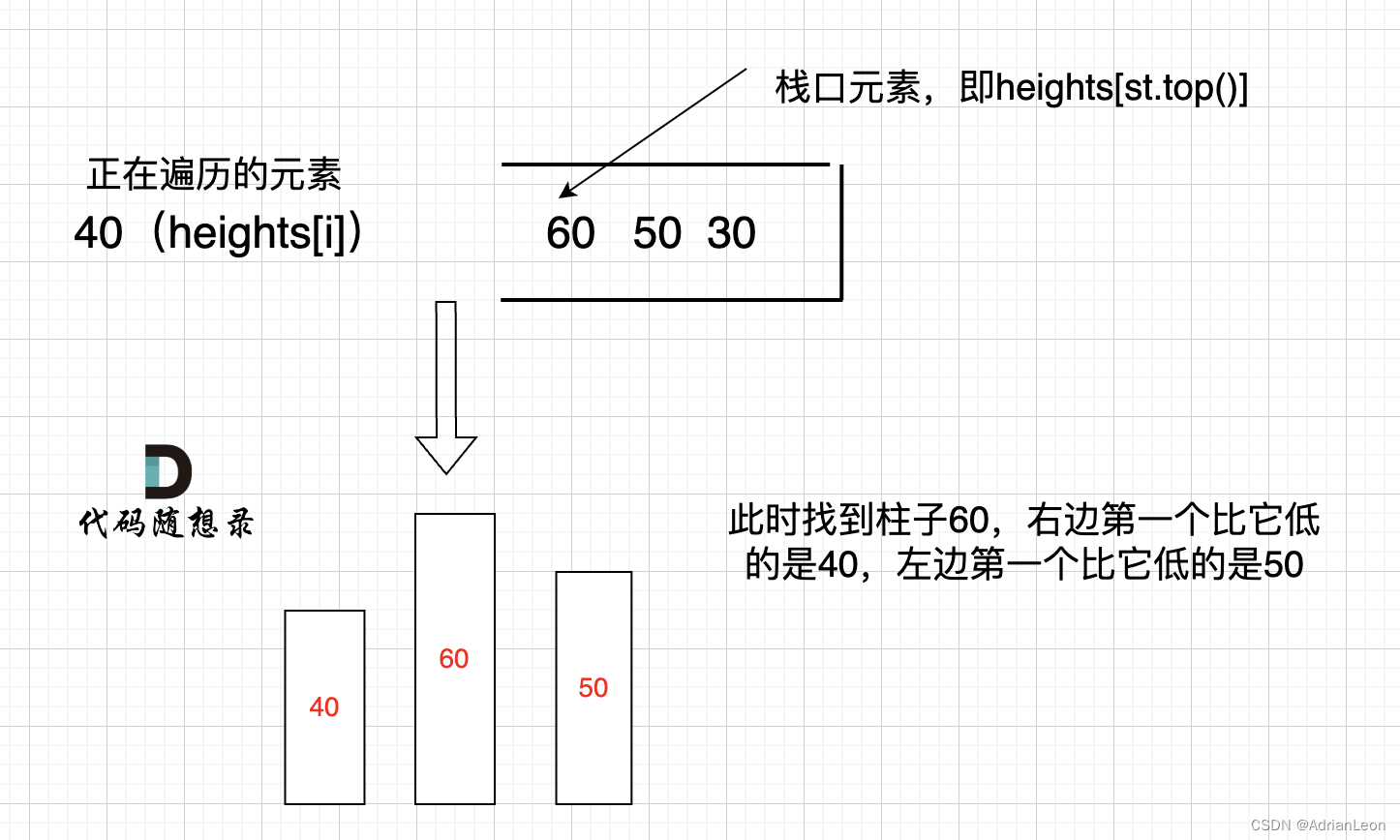
其实就是栈顶和栈顶的下一个元素以及要入栈的三个元素组成了我们要求最大面积的高度和宽度
但是首尾处都要加上一个0:
首先来说末尾为什么要加元素0?
如果数组本身就是升序的,例如[2,4,6,8],那么入栈之后 都是单调递减,一直都没有走 情况三 计算结果的哪一步,所以最后输出的就是0了。 如图:

那么结尾加一个0,就会让栈里的所有元素,走到情况三(出栈:计算面积)的逻辑。
开头为什么要加元素0?
如果数组本身是降序的,例如 [8,6,4,2],在 8 入栈后,6 开始与8 进行比较,此时我们得到 mid(8),rigt(6),但是得不到 left。
(mid、left,right 都是对应版本一里的逻辑)
因为 将 8 弹出之后,栈里没有元素了,那么为了避免空栈取值,直接跳过了计算结果的逻辑。
之后又将6 加入栈(此时8已经弹出了),然后 就是 4 与 栈口元素 8 进行比较,周而复始,那么计算的最后结果resutl就是0。 如图所示:
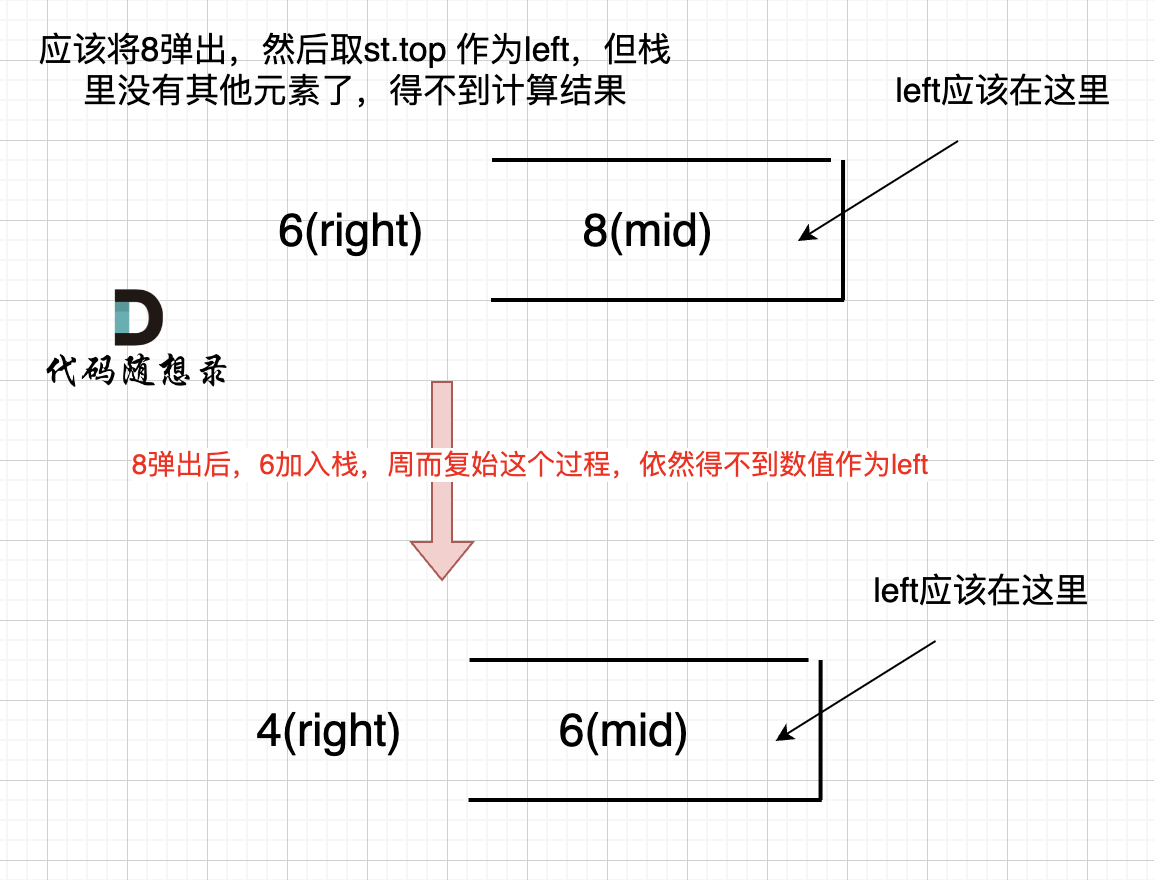
所以我们需要在 height数组前后各加一个元素0。避免原数组为单调递增或者递减的情况无法计算最大面积
这篇关于算法训练day60|单调栈part0的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!









