【林轩田】机器学习基石（八）——噪声和误差

本文主要是介绍【林轩田】机器学习基石（八）——噪声和误差，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

ppt
video

Lecture 8: Noise and Error 噪声和误差

8.1 Noise and Probabilistic Target 噪音和概率目标

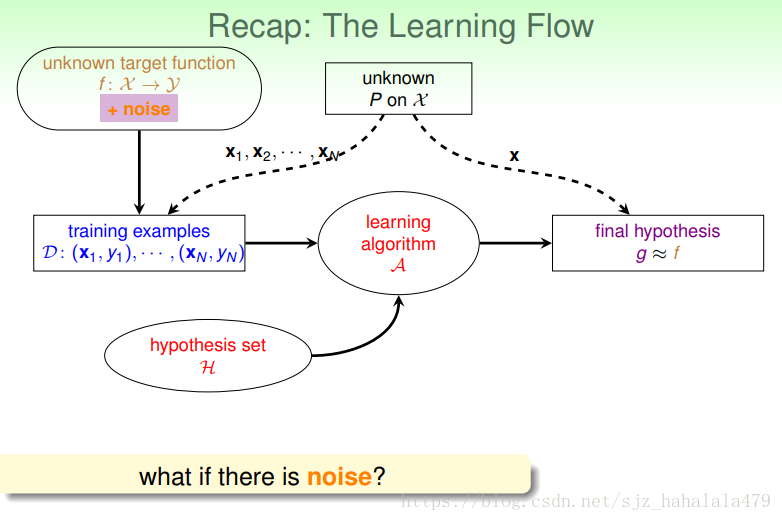
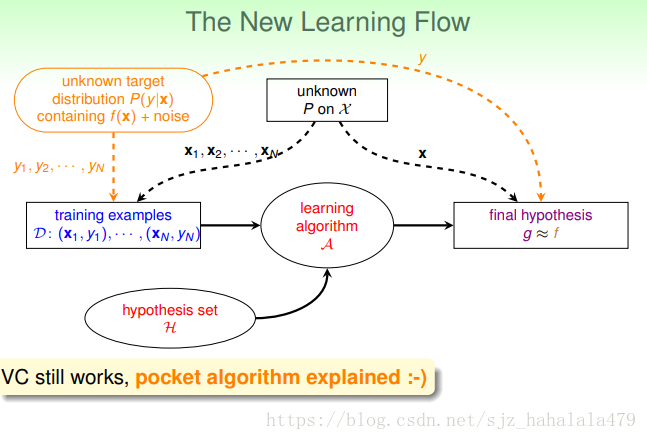
我们原有的机器学习流程如下图：

• 有一个未知的目标函数$f(x)$，还有一个未知的分布$P$，训练样本的输入$X$根据$P$生成，训练样本的输出$Y$根据$f$生成。
• 我们要给机器学习系统一个比较好的假设空间$H$，也就是说，这个$H$，要保证$d_{vc}$有限，但是$d_{vc}$也不能过小，要适当。
• 然后我们要给机器学习系统同喂一个演算法$A$，$A$会在$H$中找到它认为最接近目标$f$的$g$
• 找到这个$g$后，我们的机器学习流程就走完了。

但是，我们之前考虑的，都是没有噪声和杂质的训练数据；如果有噪声，这个机器学习流程还适用吗？我们之前计算的$vc \ bound$还适用吗？

之前在$PLA$的$pocket$算法里简短地介绍了噪声。这里，我们更加全面地描述噪声。噪声一般分为三种情况：

1. $noise\ in\ y$:被误标记的输出
2. $noise\ in\ y$:同样的输入，被标记为不同的分类
3. $noise\ in \ x$：输入特征本身不准确

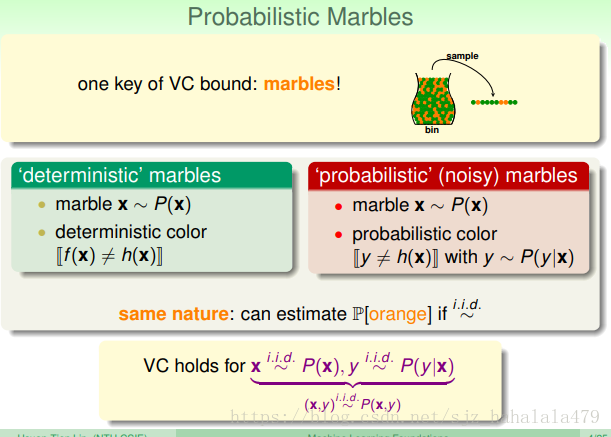
我们回过头来，看之前计算$vc \ bound\ $时，使用的“从桶中抽取橘色球和绿色球”的例子：

• 之前，从桶中取球，取出的球的颜色是确定的，即“deterministic”的。
• 之前，我们取弹珠，是按照分布$P$取的；弹珠的颜色，根据假设$h(x)$与$f(x)$是否相等，不一样，漆橘色，一样，漆绿色
• 如果加上了噪声，取出的球的颜色就不是确定的了，而是概率性的，因为我们也不知道，这个球它的颜色是本身就应该是这个颜色，还是说本不该是这个颜色，被误涂成了这个颜色。也就是说，我们无法完全通过球的颜色判断$h(x)$与$f(x)$的关系。
• 但是，由于噪声还是少数情况，所以，我们还是可以通过不同球颜色的比例来推断$h(x) \ne f(x)$的概率。
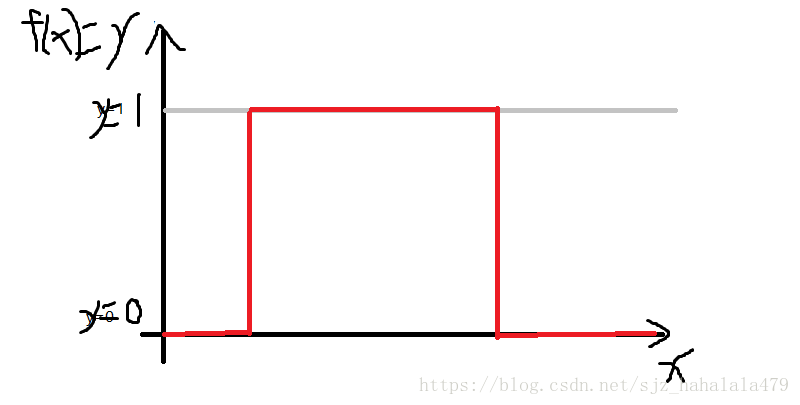
• 现在，$y$的分布是服从$P(y|x)$的。$P(y|x)$,指在$X$的条件下$Y$出现的概率分布。我们还是举二分类的例子，如果是$y=f(x)$函数分布，$y$的值只有1和0两种，即：
  
  可以看到上图，y的值只有1和0。
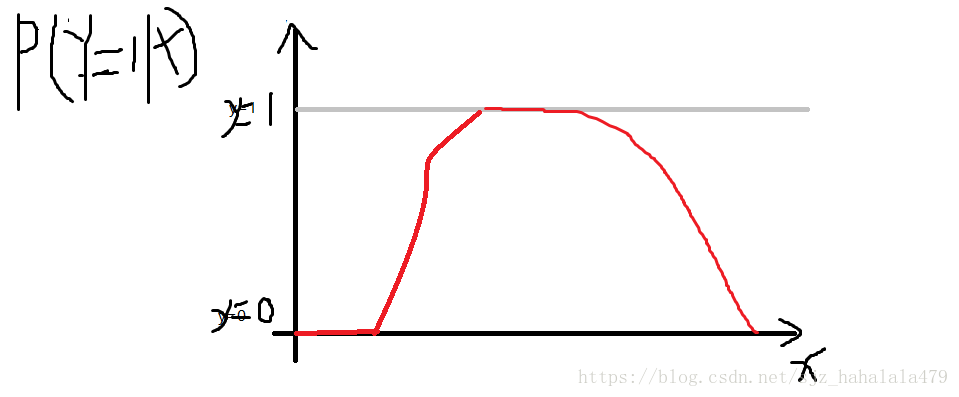
  而如果是$Y \backsim P(Y|X)$，也就是Y是服从一个条件概率分布的话，效果如图：
  

图中可以看到这个$P(Y=1|X)$的概率随着x的变化时不断变化的。我们可以看成，由于噪声的作用，使得$y=1$这件事情变得不确定起来。

• 但是，由于$y$的取值是相互独立的，也就是$Y$服从于$P(Y|X)$，且是独立同分布的；之前也说道$X$服从于分布$P$，也是独立同分布的。我们仍可以通过数学方法证明，存在噪声的$(x,y)$对，同样适用于$vc \ bound$

  

我们把$P(y|x)$叫做目标分布，这个目标分布，他描述的是，在一个$x$上，我们理想的“迷你目标”是什么。

举个图上的例子，在某个点$x$上

$$P(\circ|x) = 0.7; P(\times|x)=0.3$$
我们说，这个点的理想目标是 $f(x)= \circ$
剩下 $0.3$的概率，我们视为噪声误差。

确定的目标函数$f$，可以看作目标分布$P(y|x)$的特殊情况。
还是以“桶中橘色绿色球”为例，如果

• $y=f(x),P(y|x)$就是1
• $y \ne f(x),P(y|x)$就是0

所以，机器学习的目标变成了：
在输入$X$上，预测它的理想化迷你目标分布$P(y|x)$

所以，新的机器学习流程图如上。
它的变化，就是左上角的目标函数，变成了目标分布。

这个Fun Time问题还是很值得思考的。首先1是不对的，因为如果我们事先可以确定样本$D$是线性分割的，那么我们顺便可以确定那条线长什么样，就不需要PLA了；2也不正确，因为$D$可能有噪声的存在，使得不线性分割，但目标函数仍有可能是线性函数；3不正确的原因是，$D$样本可能存在样本偏差，万一换一个$D$就不线性可分了呢？

8.2 Error Measure 错误度量

机器学习的目标是使学习到的假设$g$尽可能地接近于目标函数$f$，如何去衡量$g和f$的相近程度呢？我们之前给出的方法是计算$E_{out}(g)$，$E_{out}(g)$越小，代表在训练样本$D$外，$g和f$的表现就越相似。

这里$E_{out}$我们使用的$g$，有三个特性

1. out-of-sample:我们考虑的$x$是训练样本外抽样的$x$或未知的$x$。
   • pointwise: 我们可以在每个点$x$上对$E$进行评估。
   • classification:我们之前限定在二元分类方法，即判断$[prediction =? target]$。我们常常把”classification error” 也叫做 “0/1 error”。

   • 更一般地，我们将$g和f$之间的错误衡量，称为$E(g,f)$。

     很多时候，我们进行错误衡量的方式，是先计算每个点上的错误度，然后把这些错误加起来，再平均，我们把这种错误衡量的方式叫做”Pointwise error measure”。

     

     如果是“in-sample”，我们的平均计算方法，就是求和再比上样本量。如果有噪声的话，这里的$f(x_n)$可以用$y_n$替换。
     如果是“out-of-sample”，我们就是计算这个分布的期望。如果有噪声的话，使用$y$替代$f(x)$；使用$P(y|x)$替代$P$。

     大多时候，使用“pointwise err”就足够了。

     有两种重要的”pointwise err”衡量方式：
     

     一种是”0/1 error”，主要用在分类问题上；
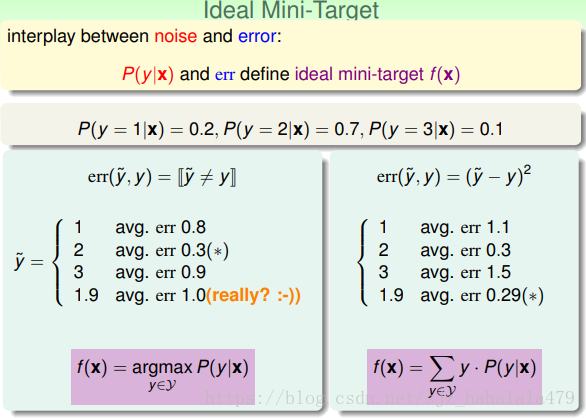
     一种是”squared error”，主要用在回归问题上。

     我们需要慎重地考虑错误衡量的选择方式。上节提到，我们为每个点$x$给出了一个理想的”mini-target”。这个点最终是如何被机器学习演算法选取出来的呢？和$P(y|x)$和”err”有关。

     

     如图所示的例子，同样的$P(y|x)$配上不同的错误衡量方式，选取的”ideal mini-target”也是不同的。
     一般来说，如果是分类问题，“ideal mini-target”是概率最大的那个$y$；而如果是回归问题，”ideal mini-target”是平均值/加权平均值。

     
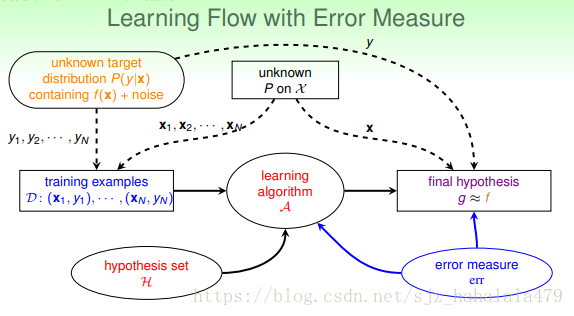
     更新后的学习流程，增加了错误衡量组件；即我们需要告诉演算法如何衡量错误。

     

     最后，林教授提到，扩展的”vc bound”对于大多数假设和错误衡量都是适用的。但是具体的推导过于繁琐和复杂，这里不再赘述。

     8.3 Algorithmic Error Measure 演算法的错误衡量

     根据不同的应用，我们需要选择不同的错误衡量方式。
     比如同样是分类问题，超市销售的指纹识别和CIA安保的指纹识别衡量是不同的。
     二元分类问题，有两种分类错误的情形。

     • false accept: 错误地接受；根据结果本来应该拒绝的，系统却错误地接受了。即$f(x) = -1, g(x) = 1$。

     • false reject:错误地拒绝；根据结果本来应该接受的，系统却错误地拒绝了。即$f(x)=1,g(x)=-1$。

     • 下图是描述二元分类四种情况的混淆矩阵。

       

       “0/1 error “对两种类型的错误等价地进行处罚。

       但是如上文所说，不同的分类问题，错误衡量的方式是不同的。

       • 比如，超市打折：一个顾客被错误地拒绝打折，和一个顾客被错误地接收打折，给超市带来的损失是不同的。错误地拒绝，顾客会很生气，超市会损失客源；错误地接受，超市只是少赚点钱，而且可以通过另外的渠道追回损失。这样看来，给”false reject”类型的错误应该设置更高的权重，因为犯这种错误的损失更大。
       • 如果是CIA门禁系统识别人员呢。一个人员被错误地接收进入系统，比一个人员被错误地拒绝进入系统，造成的损失大多了。所以，这种情形，给”false accept”类型的错误，应设置更高的权重。

       

       所以，我们说：错误衡量”err”是依赖于应用的，也是依赖于客户的选择的。在设计演算法的错误衡量$\hat{err}$时

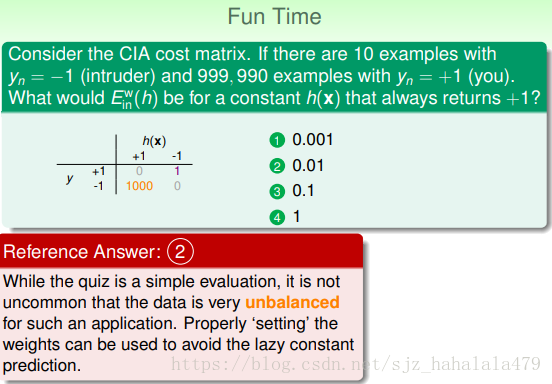
       • 最好的情形就是需要什么样的错误衡量”err”，就让$\hat{err} = err$即可。但是，很多时候，无法使用“err”作为我们的$\hat{err}$。因为，客户一般很难将自己需要的“err”用数学化的语言表现出来。比如，我们跑去问CIA，“false accept”错误的权重你们觉得多少合理，1000或5000？他们自己其实也没概念。
       • 所以，在设计演算法的$\hat{err}$时，通常采用替代的办法。有两种替代方式，一种是plausible的，即说服我们自己的有意义的错误替代：
         
         • “0/1 error”：之前有提到，使用这种错误衡量方法。是最小化”flipping noise”。
         • “squared error”：如果我们相信噪声服从高斯分布，那么我们可以通过最小化“Gaussian noise”来最小化错误度。
       • 但是，“0/1 error”的优化是NP hard的，不好优化。我们可以选用另一种friendly的替代方式，方便优化。
         
         • 凹凸函数
         • 封闭的解

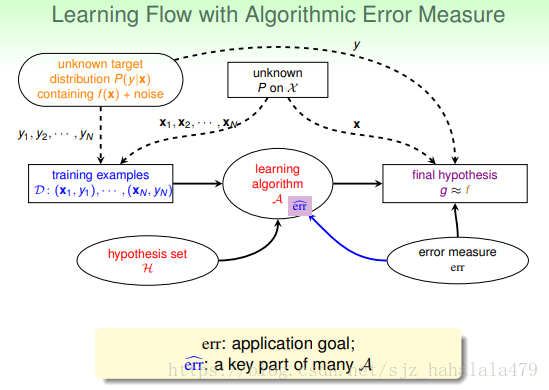
       现在我们将系统的学习流程再做一个更新。加入了$\hat{err}$。这里$err$是我们真正的错误衡量目标；而$\hat{err}$是我们认为的$err$的有效替代。

       

       8.4 Weighted Classification 带权重的分类

       在二元分类中，根据不同的应用情景，有不同的错误衡量方式。对于“false reject”和“false accept”两种类型的错误，也会赋予不同的权重。
       

       这种带权重形式的分类问题，应该如何学习呢？
       

       直观的想法是

       • PLA可以直接用。因为我们没有改变样本的分布，只要样本线性可分，我们总能使找到$E_{in} = 0$的那条线。
       • 大多数情况样本会有噪声，这时候要用到pocket。pocket算法修改一部分步骤也可以直接用。
         
         • 就是当$w_{t+1}$得到了比$\hat{w}$更小的$E_{in}^{w}$时，将$w_{t+1}赋给\hat{w}$。这里其实就是用新的$E_{in}^{w}$替代了元算法中的$E_{in}^{0/1}$。
         • 虽然我们直观上认为这样做是没问题的。但是我们能给出理论上的证明吗？

       

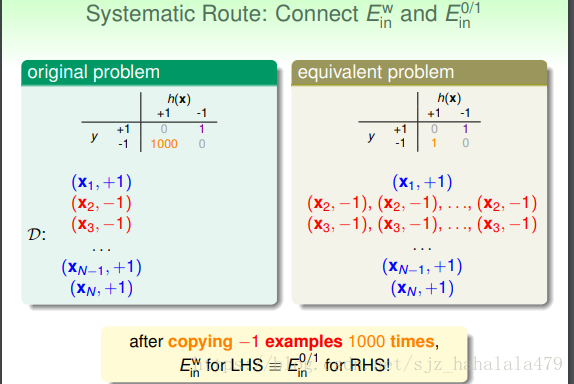
       如图，我们可以看到，将$y=-1$的点复制1000遍后（即扩大了数据样本空间$D$），左式的$E_{in}$和右式是相等的。

       

       但是，直接copy（硬拷贝）很费计算机空间。我们可以使用“虚拷贝”的方法，在概率上给check到“-1”样本的机会扩大1000倍，这样使用“weighted pocket algorithm”，我们就可以解决“weighted classification”的问题。

       

       Fun Time这个问题涉及到机器学习实战中的很普遍的一个情景，就是正负样本不平衡。调整正负样本的权重是一个很有效的解决方式。

这篇关于【林轩田】机器学习基石（八）——噪声和误差的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---