动态规划略有所得数字三角形(POJ1163)

本文主要是介绍动态规划略有所得数字三角形(POJ1163)，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

(二) POJ1163，DP的入门级题目。和上面的POJ1088有些相似，也可以看成从上往下滑。不过起点是确定的，只能( 1, 1 )开始。

题目分析：

要使和最大，关键是确定终点。不妨设以( i, j )为起点，现在求滑行的最长路径。

如果( i, j )为终点，则前一个点只可能是( i-1, j-1 )或者( i-1, j )。选择的标准，还是看哪个点更优。如果假设( i, j )--->( i-1, j-1 )，则问题又变成了：以( i-1, j-1 )为终点求最大和的问题。

状态转换方程：

dp( i,j ) = Max( dp( i-1, j-1 ), dp( i-1, j) ) + data[i][j];

其中：dp( i,j )表示以( i, j )为终点，所得到的最大和。

data[i][j]表示三角矩阵中第i行第j列的值

编程实现：

同样，要注意三角矩阵的边界。边界的有些点不能用状态方程就去。如图2所示，(3,1)和(3,3)要单独处理。

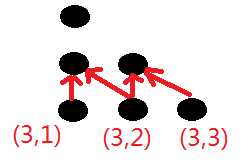
在上面的数字三角形中寻找一条从顶部到底边的路径，使得路径上所经过的数字之和最大。路径上的每一步都只能往左下或右下走。只需要求出这个最大和即可，不必给出具体路径。三角形的行数大于1小于等于100，数字为 0 - 99

输入格式：

5 //表示三角形的行数接下来输入三角形

Sample Output

这道题属于入门级DP，从下往上计算比较方便，递推公式F[i][j]=max{F[i+1][j],F[i+1][j+1]}+num[i][j]，初始把最后一行数据赋给F数组，或者直接在num数组上计算。。。

从下至上，首先计算最底层。底层是无需计算的，保存即可。

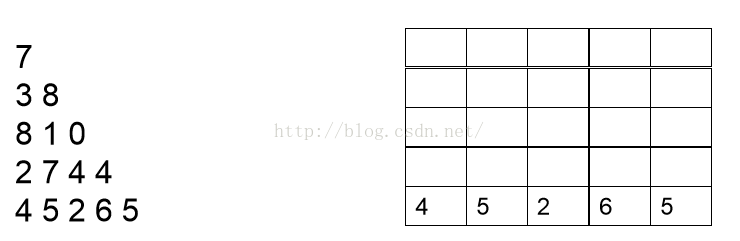
下一步计算倒数第二层。


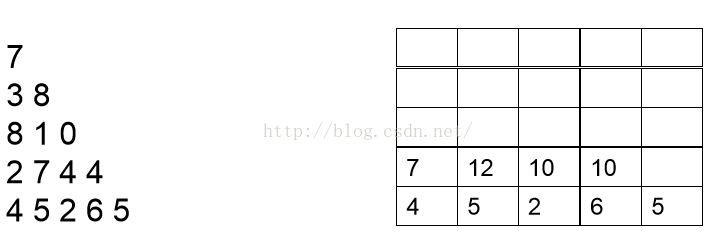
import java.util.Scanner;/*这道题属于入门级DP，从下往上计算比较方便，递推公式F[i][j]=max{F[i+1][j],F[i+1][j+1]}+num[i][j]，初始把最后一行数据赋给F数组，或者直接在num数组上计算。。。
这个算法是从最后一层开始向上进行计算输入 
5
7
3  8
8  1  0
2  7  4  4
4  5  2  6  5输出
30  
23  21  
20  13  10  
7  12  10  10  
4  5  2  6  5  */
public class TheTriangle
{public static void main(String[] sure){Scanner sc = new Scanner(System.in);int n = sc.nextInt();int[][] num = new int[n][n];int[][] cal = new int[n][n];int i = 0;// 初始化while (i < n){int j = 0;while (j <= i){num[i][j] = sc.nextInt();j++;}i++;}// 先把最后一列赋值过去给calfor (int j = 0; j < n; j++){cal[n - 1][j] = num[n - 1][j];}for (int j = n - 2; j >= 0; j--){for (int k = n - 2; k >= 0; k--){cal[j][k] = Math.max(cal[j + 1][k], cal[j + 1][k + 1]) + num[j][k];}}//打印出结果，其中第一行数字就是结果的值int i1 = 0;while (i1 < n){int j1 = 0;while (j1 <= i1){System.out.print(cal[i1][j1]+ "  " );j1++;}System.out.println();i1++;}System.out.println(cal[0][0]);}
}

这篇关于动态规划略有所得数字三角形(POJ1163)的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！