本文主要是介绍算法导论复习——CHP22 分支限界法,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
LIFO和FIFO分枝-限界法
采用宽度优先策略,在生成当前E-结点全部儿子之后再生成其它活结点的儿子,且用限界函数帮助避免生成不包含答案结点子树的状态空间的检索方法。两种基本设计策略: FIFO检索:活结点表采用队列;LIFO检索:活结点表采用栈。
如采用FIFO分支-限界法检索4-皇后问题的状态空间树:

LC-检索(Least Cost,A*算法)
LIFO和FIFO分枝-限界法存在的问题
对下一个E-结点的选择规则过于死板。对于有可能快速检索到一个答案结点的结点没有给出任何优先权,如结点30。
解决:做某种排序,让可以导致答案结点的活结点排在前面 。
如何排序? 寻找一种“有智力”的排序函数C(·),来选取下一个E 结点,加快到达一答案结点的检索速度。
如何衡量结点的优先等级?
对于任一结点,用该结点导致答案结点的成本(代价) 来衡量该结点的优先级——成本越小越优先。
对任一结点X,可以用两种标准来衡量结点的代价:
1)在生成一个答案结点之前,子树 X 需要生成的结点数。
2)在子树 X 中离 X 最近的那个答案结点到 X 的路径长度。
C(x)
“有智力”的排序函数,依据成本排序,优先选择成本最小的活结点作为下一个E结点进行扩展。 C(·)又称为“结点成本函数” n 结点成本函数C(X)的取值:
1)如果X是答案结点,则C(X)是由状态空间树的根结点到X 的成本(即所用的代价,可以是级数、计算复杂度等)。
2) 如果X不是答案结点且子树X不包含任何答案结点,则 C(X)=∞
3) 如果X不是答案结点但子树X包含答案结点,则C(X)应等于子树X中具有最小成本的答案结点的成本。
计算结点X的代价通常要检索子树X才能确定,因此 计算C(X)的工作量和复杂度与解原始问题是相同的。 n 计算结点成本的精确值是不现实的——相当于求解 原始问题。怎么办? n 结点成本的估计函数包括两部分:h(X)和
是由X到达一个答案结点所需成本的估计函数。
性质:单纯使用选择E结点会导致算法偏向纵深检查。
故引进h(X)改进成本估计函数:h(x)=根结点到结点X的成本——已发生成本。
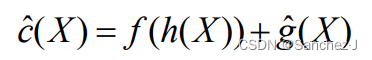
f(·)是一个非降函数。 非零的f(·)可以减少算法作偏向于纵深检查的可能性, 它强使算法优先检索更靠近答案结点但又离根更近的结点。
LC-检索:选择值最小的活结点作为下一个E-结点的状态空间树检索方法。
特例:
BFS: 依据级数来生成结点,![]() ;
;
D-Search:令f (h(X)) =0;所以当Y是X的一个儿子时, 总有![]() ;
;
LC分支-限界检索:带有限界函数的LC-检索

LEAST(E):在活结点表中找一个具有最小成本估计值的活结点,从活结点表中删除这个结点,并将此结点放在变量E中返回。
ADD(X):将新的活结点X加到活结点表中。
活结点表:以优先队列存放
不同估算函数对于结果的影响
1、当估算的距离等于实际距离时,一路下去,肯定就是最优的解,而且基本不用扩展其它的点。
2、如果估算距离小于实际距离时,则到最后一定能找到一条最短路径,但是有可能会经过很多无效的点。(过于乐观,以h(X)为主)
3、如果估算距离大于实际距离时,有可能就很快找到一条通往目的地的路径,但是却不一定是最优的解。(过于悲观,以g(X)为主)
成本函数在分支-限界算法中的应用
假定每个答案结点X有一个与其相联系的c(X),且找成本最小的答案结点。
1)最小成本的下界为X的成本估计函数。当![]() 时,
时, 给出了由结点X求解的最小成本的下界,作为启发性函数,减 少选取E结点的盲目性。
2)最小成本的上界 。最小成本的上界 定义U为最小成本解的成本上界,则对具有![]() 的所有活结点可以被杀死,从而可以进一步使算法加速,减少求解的盲目性。
的所有活结点可以被杀死,从而可以进一步使算法加速,减少求解的盲目性。
最小成本上界U的求取:
1)初始值:利用启发性方法赋初值,或置为∞
2)每找到一个新的答案结点后修正U,U取当前最小成本值。 注:只要U的初始值不小于最小成本答案结点的成本,利用U就不会杀死可以到达最小成本答案结点的活结点。
利用分枝-限界算法求解最优化问题
可行解:类似于n-元组的构造,把可行解可能的构造过程用 “状态空间树”表示出来。
最优解:把对最优解的检索表示成对状态空间树答案结点的 检索。
成本函数:每个结点赋予一个成本函数c(X) ,并使得代表最优解的答案结点的c(X)是所有结点成本的最小值 。
这篇关于算法导论复习——CHP22 分支限界法的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








