详解卡尔曼滤波（Kalman Filter）

本文主要是介绍详解卡尔曼滤波（Kalman Filter），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

1. 从维纳滤波到卡尔曼滤波

黑盒（Black Box）思想最早由维纳（Wiener）在1939年提出，即假定我们对从数据到估计中间的映射过程一无所知，仅仅用线性估计（我们知道在高斯背景下，线性估计能达到克拉美劳下界，是最优估计）来掩盖我们的无知。

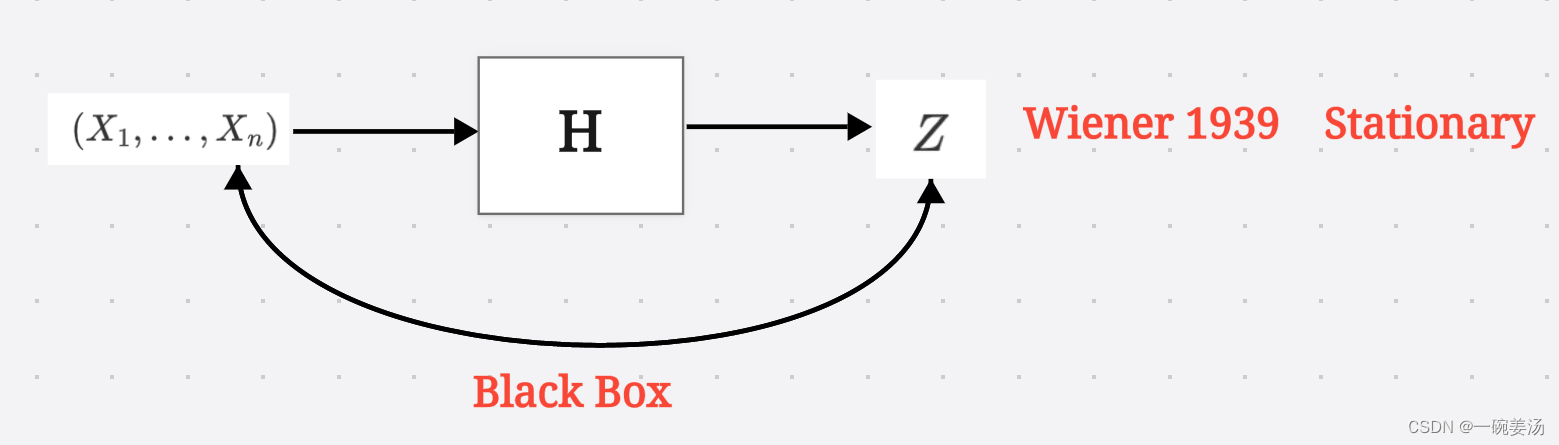
但是，到了二十年以后的1960年卡尔曼的年代，我们对于红框内的事（prior knowledge），很有可能是知道的，并且知道得很详细，很清楚。再这样的情况下，我们还不能有效地利用这一部分先验知识来帮助我们把估计做的更好就没有任何道理了。卡尔曼就是从红框入手，将这部分先验信息表达出来。至于怎么表达，就用到了状态空间表达（State Space Representation）

2. 状态空间表达（State Space Representation）

我们可以写出如下一组方程：

$\begin{cases}Z_n=g(Z_{n-1},v_n) & \mbox{State \ Equation}\quad (\mbox{Non-observable}) \\ X_n=h(Z_n,w_n)& \mbox{Observation\ Equation} \end{cases}$

状态方程（State Equation）：是决定研究对象行为的关键量 $Z_n$ 随时间的变化情况。 $Z_n$ 我们是不能直接观测到的（因为采样的时候根本采不到这些状态，状态是隐含在观测量背后的）；
观测方程（Observation Equation）：是状态 $Z_n$ 通过某种形式、窗口、途径，让我们看到关于它的某种表现，而这种表现反映在观测量 $X_n$ 当中。 $X_n$ 是我们能直接观测到的。

由此可以发现，从维纳到卡尔曼有两点本质区别：

状态空间表达是我们注入先验知识的重要窗口，自此黑箱变成了白箱（White Box）：因为数据 $\{X_n\}$ 和估计量 $\{Z_n\}$ 之间的关联关系已经完全展现在我们的面前了。
$Z_n$ 为时变的（Time varied），这就使得问题从平稳（Stationary）的变为非平稳的（Non-Stationary）的。

值得一提的是：状态空间表达还有别的称呼，比如HMM（Hidden Markov Model）隐马尔科夫模型。

3. 界定滤波问题

首先把状态空间表达进一步细化：

$\begin{cases} Z_n=G_nZ_{n-1}+v_n\\ X_n=H_nZ_n+w_n \end{cases}$

$\quad E(v_n)=E(w_n)=0,Cov(v_n)=R_n,Cov(w_n)=S_n ,$

$\{v_n\},\{w_n\} \mbox{ are Independent both and between}$

在此线性基础上我们来界定卡尔曼滤波的滤波问题：

这里解释一下图里的逻辑脉络：

我们想用 $(X_1,...,X_n)$ 估计 $Z_n$ ；
虽然我们知道，条件期望是均方意义下的最优估计，但是通常在非高斯背景下我们很难求出条件期望；
于是我们转而去求一个最优线性估计，本质也就是把 $Z_n$ 投影到由 $(X_1,...,X_n)$ 张成的线性子空间里；
$z_{n|n}$ 中两个 $n$ 的含义：第二个 $n$ 表示用 $x_1,...,x_n$ 的数据，第一个 $n$ 表示要估计的状态是 $z_n$ 。做的是线性估计，也就是上面说的投影。
卡尔曼滤波为了实现 $z_{n|n}\leftarrow z_{n-1|n-1}$ ，采用了两步走策略：第一步预测（Prediction）；第二步矫正（Correction）。所以该策略也被称为预测-矫正（Prediction-Correction）策略。

4. 推导细节

上面这里头核心的一步就是正交化，因为xn 和 x(1:n-1) 当然不正交，因为如果正交的话，就是高斯白噪声了。除非设备坏了，不然采出来的数据几乎不可能是个白噪声。

可以看到，方差不断地减小，这个过程是自适应完成的，非常精巧。

5. 卡尔曼滤波总结

大名鼎鼎的卡尔曼滤波可以总结如下：

6. 理论应用

卡尔曼滤波怎么用呢？只需要给定初值 $\Sigma_{0|0}=I$ ，（其实初值取什么不太重要别是0就行），和参数取值 $G_n,H_n$ ，就可以随着数据的到来不断递推下去，获得越来越精准的结果，因为数据当中的信息是会不断地吸收进你的滤波器当中，这个其实也就是机器学习。

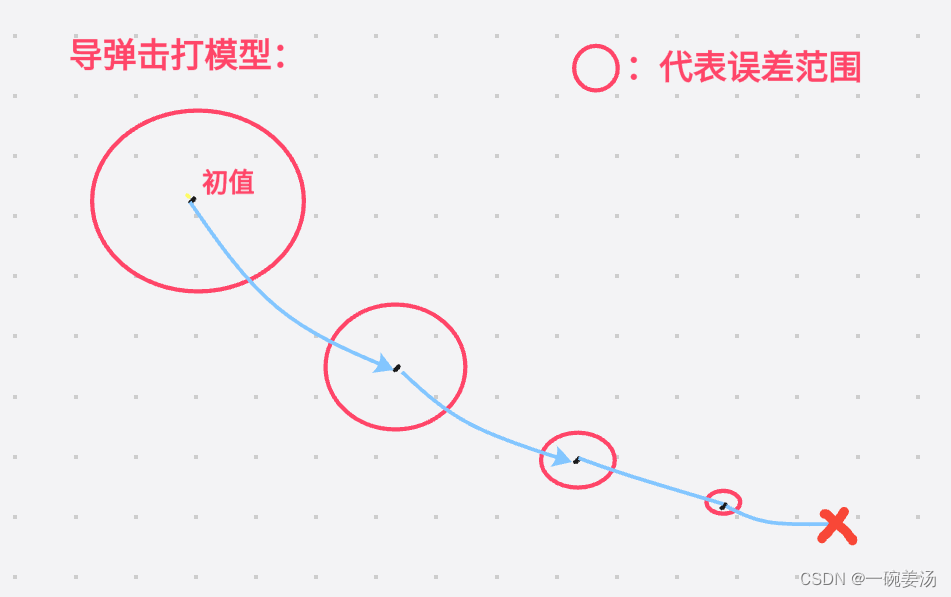
追踪模型（Target Tracking）： $[Z_n,Z_n^{'},Z_n^{''}]$

状态方程：

假设物体做匀加速直线运动：

$\left[\begin{matrix} Z_n\\ Z_n^{'}\\ Z_n^{''} \end{matrix}\right] =\left(\begin{matrix} 1&\Delta t&\frac{1}{2}(\Delta t)^2\\ 0&1&\Delta t\\ 0&0&1 \end{matrix}\right) \left[\begin{matrix} Z_{n-1}\\ Z_{n-1}^{'}\\ Z_{n-1}^{''} \end{matrix}\right] +v_n$

观测方程：

$X_n=[1,0,0]\left[\begin{matrix} Z_n\\ Z_n^{'}\\ Z_n^{''} \end{matrix}\right]+w_n$

7. 卡尔曼滤波的优缺点（Pros and Cons）

我们平常形容某一门信号处理技术或者别的什么技术成熟了，是什么意思？

要知道成熟绝不等于热门，热门的意思是：现在研究的人特别的多，文章特别多，对于这个方法的各种各样的扩充改进更新等等层出不穷，这个叫热门，但这个时候一定是不成熟的，原因很简单，是因为大家还没有看到这个方法的缺点。当大家知道的不仅仅是它能干什么，还有它不能干什么，那么这个方法就成熟了。卡尔曼滤波的缺点主要体现在以下三个方面：

1. 模型失配（Model Mismatch）

卡尔曼滤波说到底，虽然后面的推导看起来那么复杂，但其实就干了正交化这一件事而已。

另一方面，卡尔曼滤波极度依赖状态空间表达。在上述的追踪模型中，如果物体做的不是匀加速直线运动，是由模型失配导致 $Z_{n|n}$ 中的误差项 $(X_n-H_nZ_{n|n-1})$ 增大，而卡尔曼滤波却依旧坚持认为这个误差项是由于噪声造成的，并且不断增大卡尔曼增益，导致错上加错，最后乱套。

对付模型失配，有一个技术叫做IMM（交互式多模型Interacting Multiple Models），其实就是准备了很多个模型，总有一款适合你。模型之间有交互，是为了确认你究竟处于哪个模型当中。

2. 非线性（Non-Linear）

卡尔曼滤波线性性。但是现实情况大多是非线性的：

$\begin{cases} Z_n=g(Z_{n-1},v_n)\\ X_n=h(Z_n,w_n) \end{cases}$

比如，导航信号在穿过大气层的时候，是会有很严重的电离层的散射和畸变。（因为导航星很高，要飞两万公里以上过大气层，没到3万6的同步轨道，也不是几百公里侦查星）具有很强的非线性。那么，在非线性的情况下如何使用卡尔曼滤波？

一个很简单的办法就是线性化：EKF（扩展的卡尔曼滤波 Extended Kalman Filtering）

$\begin{cases} Z_n=J_g^{(1)}Z_{n-1}+J_g^{(2)}v_n)\\ X_n=J_h^{(1)}Z_n+J_h^{(2)}w_n) \end{cases}$

线性化只能局部做，所以模型要隔一段时间变一下，很正常。

3. 分布本身的推演（Distribution Propagation）

我们知道高斯能够完全由均值和方差确定，而卡尔曼滤波推演的只有均值和协方差阵，是因为我们假设噪声是高斯分布。要是噪声的情况非高斯，我们面临每一时刻，状态的分布情况都不一样，所以我能不能设计一种方法，使得这个状态的分布本身（不是一阶矩、二阶矩）能够随时间演化。这个问题，人们也解决了，靠的是粒子滤波技术（Particle Filtering）

这篇关于详解卡尔曼滤波（Kalman Filter）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！