本文主要是介绍leetcode 474. Ones and Zeroes | 474. 一和零(双约束背包问题),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
题目
https://leetcode.com/problems/ones-and-zeroes/
题解
这是一个双约束的背包问题。此题需要的前置知识,可以参考我之前的博客:算法设计与分析 0-1背包问题 动态规划解法【超详细】
针对本题,思路如下:
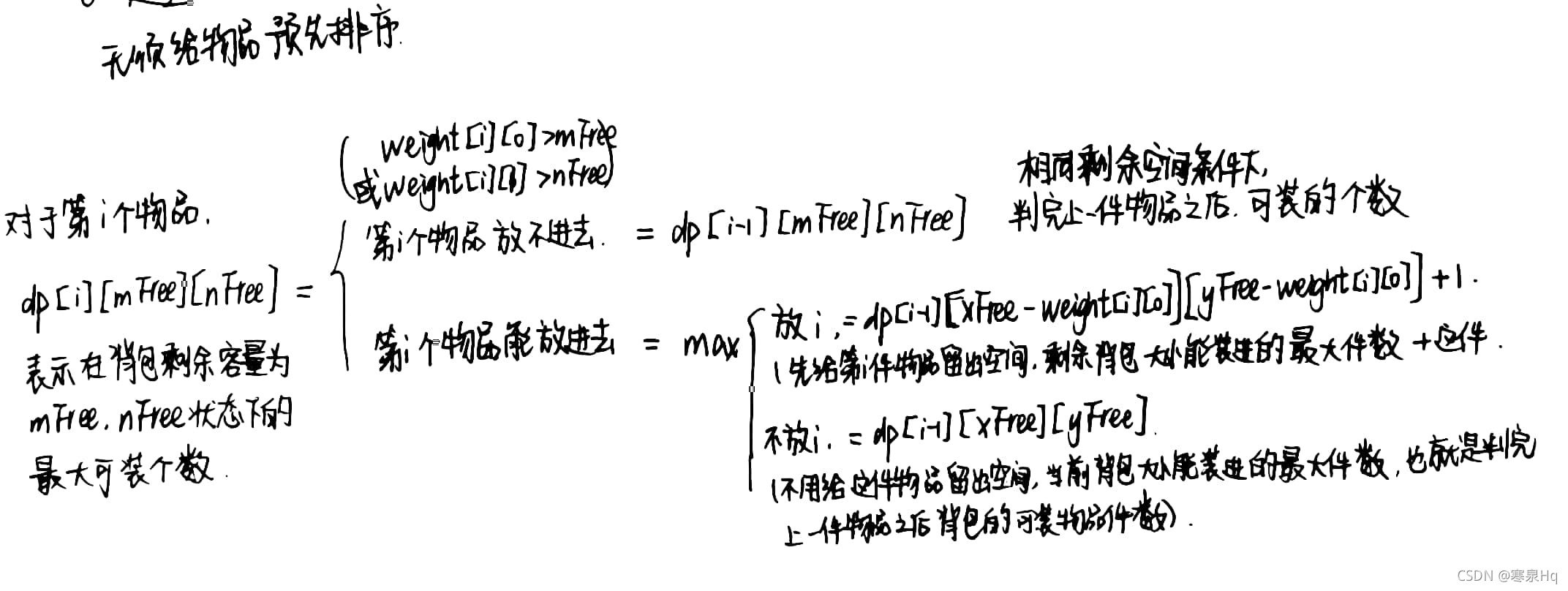
在实现上,为了避免 i-1 的越界判断,将整个数组的 i=0 位置空出来,显得更整洁一些。
class Solution {public int findMaxForm(String[] strs, int m, int n) {int L = strs.length;int[][] weight = new int[L + 1][2];for (int i = 0; i < L; i++) {int z = 0;int o = 0;for (int j = 0; j < strs[i].length(); j++) {if (strs[i].charAt(j) == '0') {z++;} else {o++;}}weight[i + 1][0] = z;weight[i + 1][1] = o;}int[][][] dp = new int[L + 1][m + 1][n + 1];for (int i = 1; i <= L; i++) { // 第i个物品(序号从1开始)for (int mFree = 0; mFree <= m; mFree++) { // 背包剩余x容量for (int nFree = 0; nFree <= n; nFree++) { // 背包剩余y容量if (weight[i][0] > mFree || weight[i][1] > nFree) {dp[i][mFree][nFree] = dp[i - 1][mFree][nFree];} else {dp[i][mFree][nFree] = Math.max(dp[i - 1][mFree - weight[i][0]][nFree - weight[i][1]] + 1, dp[i - 1][mFree][nFree]);}}}}return dp[L][m][n];}
}

这篇关于leetcode 474. Ones and Zeroes | 474. 一和零(双约束背包问题)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!









