本文主要是介绍背包密码体制原理大白话讲解及Python实现,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
一、背包密码体制介绍
提到背包密码体制,我们首先就想到为什么这个密码体制和背包有什么关系,背包二字的由来是因为在1978年Merkle与Hellman提出的MH背包问题,这个问题的总体思路是这样的,现在有许多不同重量的物体,从中可以任意选择n件物品放入背包。披露背包中物品的总重量和物品堆;但是所选项目的类型不是公开的。针对这种问题Merkle与Hellman合作设计了一种使用背包问题对信息进行加密的方法,因为该加密算法涉及到背包问题,所以背包密码因此得名。
二、背包加密算法原理
背包加密算法的总体思路是这样的,假如A想发送一条信息,A首先要具有私钥,并且该密钥是通过背包问题传递的,该私钥可以生产一个公钥,发送消息之前必须先使用公钥进行加密,消息的合法接收者使用私钥等已知信息进行解密,这就是背包加密算法的总体思路。
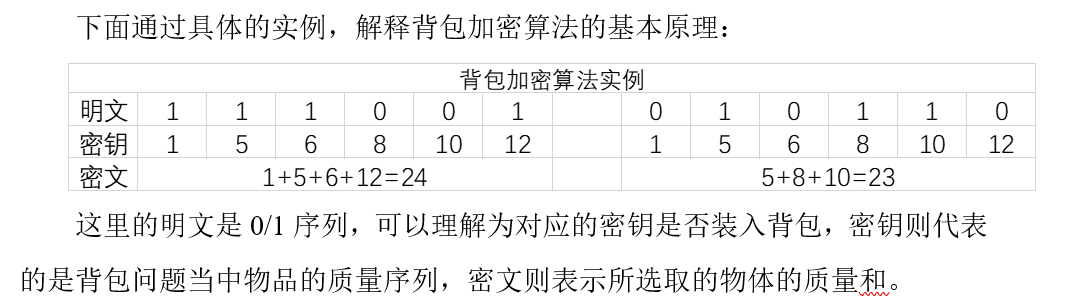
三、背包加密算法步骤
3.1 构造递增序列背包
在背包问题当中,若物品的重量列表是一个超递增序列,这个问题是很容易的出答案的,解决超递增序列的背包问题主要有以下几个步骤:假如有一个背包,背包的重量已知,将这个背包的重量与我们已知的超递增序列中的最大值进行比较,如果背包的重量小于这个数,那么这个数不在背包中,如果重量大于或等于这个数,那么这个数在背包中,用背包的重量减去这个数,得出的结果继续与序列中的下一个数进行比较,重复比较直到比较完为止。如果背包的总重量减到0则该背包问题得出解,反之则无解。

3.2 以私钥为基础构造公钥

3.3 使用公钥进行加密
通过以私钥为基础构造公钥,此时当我们拿到公钥的时候,我们开始使用公钥进行加密数据,假如我们拿到一个二进制的数据011000110101101110,背包加密算法对该二进制数据加密的主要流程是:


3.4 解密
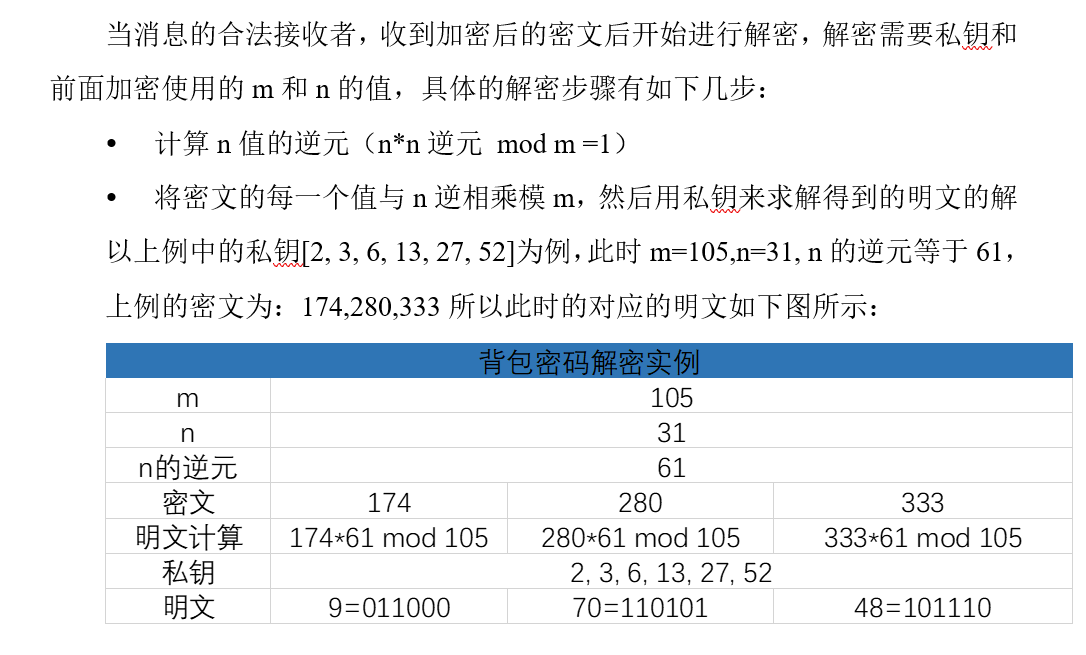
四、背包密码体制Python实现
4.1 以私钥构造公钥
def create_pubkey(data):# 构造m 此时m应大于超递增序列的所有和# m = sum(data) + 2# m = 250m =<这篇关于背包密码体制原理大白话讲解及Python实现的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






