本文主要是介绍文章:LIME:Why Should I Trust You?,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
本文结合文章 “Why Should I Trust You?” Explaining the Predictions of Any Classifier 主要阐述一下内容:
- LIME 算法意义
- LIME 算法原理
- LIME 算法效果
原文参见:https://arxiv.org/pdf/1602.04938v1.pdf
一、LIME 算法意义
LIME 是解释模型的算法,目的为了解模型的预测原理。所以 LIME 算法意义即为解释模型的意义。
1. 信任模型及其预测结果
信任问题涉及到两个方面:1. 信任模型,2. 信任预测结果。我们可以通过验证集来评估模型整体的预测精度,但却无法判定模型对测试集中特定样本的预测是否准确。而在如医疗诊断等许多领域中,误判所带来的风险太大,只知道模型的预测精度是不足够的,从业者还需要知道每次预测的判据是什么,来分析预测结果是否可靠。所以即使模型预测准确率达到95%,许多领域的从业者也是不敢使用的。所以,解释模型可以令使用者信任模型及其预测结果,有助于算法、模型的推广。
2. 提高判断模型优劣的准确性
一方面,由于诸多因素限制,训练集、验证集、测试集往往都是有偏的,但却难以被察觉。另一方面,训练集与验证集、测试集之间可能存在一定程度的无意的数据泄露,即验证集、测试集中包含一部分训练集。所以在验证集和测试集上效果良好的模型未必在实际应用中也效果良好。同时,由于模型中计算和优化的指标(如准确性)与实际关注的指标之间可能是不匹配的。所以,仅通过预测精度来判断模型的优劣是不充分的,还需要了解模型的预测原理,根据先验知识,选择在实际应用中可能效果更优的模型。
例1:下图展示了用 LIME 算法对不同模型预测同一样本的结果的分析。两个模型均是由 SVM 算法在 20 个新闻组数据集上做训练得到的分类器,用于区分文章主题是 “基督教” 还是 “无神论” 。条形图的长短表示特征(单词)对预测结果的贡献,越长说明贡献越大;颜色表明了特征对预测结果类别的贡献,紫红色表明该单词的出现有助于模型预测文章的主题是 “无神论”,而绿色则表明 “基督教”。

Algorithm 2 模型在测试集上的准确度为 94%,而 Algorithm 1 的准确度较低。如果只以准确度作为评判模型优劣的标准,那么 A2 优于 A1。但我们在知晓模型的预测原理后发现,A2 中对预测有帮助的特征都是与 “基督教” 或 “无神论” 无关的词,如 Posting,Host,Re。经研究发现,训练集中有 22% 的样本包含 Posting,而其中 99% 是 “无神论” 标签,所以 A2 学到了特征 Posting。相对的,A1 则找到的最重要的单词是 GOD,这使得使用者更愿意相信低精度的 A1 在实际中会有更好的表现。从本例中可以看出,通过对模型预测结果的分析,不仅可以选择出更优秀的模型,同时能发现训练集是有偏的。
3. 提高模型预测精度
对于如预测植物株高、产量等这类预测任务,由于经费问题,生物学数据面临着鱼和熊掌不可兼得的问题:数据多样性与排除无关变量无法兼得。若测定的样本集中于一个群体,则变量控制的好,无种群结构,但训练出来模型的迁移能力差,难以预测其他群体样本的表型;若测定的样本集多样性高,如以种质库作为训练集,则训练出来的模型迁移能力强,但由于无法排除无关变量,预测精度不高且找到的可能是与群体结构相关的SNP位点。所以需要研究者通过先验知识手动去除被模型重用的无关变量,重新训练,提高模型的预测精度。
4. 挖掘重要特征,研究现象形成的内在原因
二、LIME 算法原理
LIME 全称 Local Interpretable Model-Agnostic Explanations,是以使用者可理解(Interpretable)的方式解释(Explanations)任何类型(Model-Agnostic)的模型的预测结果(Local)的算法。可以发现,LIME 算法只提到了如何解释模型的预测结果,而没有提及如何解释模型。作者通过次模采样的方法,以样本代表总体的思路,完成对模型整体的解释。下面分别对 LIME 的可理解、模型无关、局部吻合和次模采样进行介绍。
1. 可理解(Interpretable)
首先,对模型预测结果的解释能被人们所理解。由于人类理解能力有限,LIME 通过以下 4 个方面达到模型及预测结果可被理解的目的
- 模型足够简单,如线性模型,各项之间是加性关系,每项的重要性以权重体现,易于理解。
- 特征足够简单。无论特征在模型中如何被使用,如词嵌入,LIME 只用 “存在” 或 “不存在” 表示特征并解释预测结果。若样本 x 在原模型中的值域为 x ∈ Rd,则在 LIME 算法构建出的新模型中 x′ ∈ {0,1}d′。其中 d、d′ 表示维度,x ∈ Rd 表示 x 是 d 维向量,各维度的值域为实数 R,x′ ∈ {0,1}d′ 表示 x′ 是 d′ 维向量,各维度的值域为 {0,1}。注意,由于模型 f 内部对特征的利用未必是人们容易理解的特征,而 LIME 使用人们方便理解的形式来解释预测结果,所以 d 可能 ≠ d′。如处理文本时,f 使用词嵌入加工输入特征进行预测,d = 词嵌入的维度,而 LIME 对预测结果进行解释时,使用的是文章中包含哪些单词,d′ = 训练集中总单词数(相同单词只计数一次),参见 fig 1。
- 特征数足够少,特征之间的关系足够简单。假设预测结果由100个特征所构成,部分特征之间还存在相关性,构建出来的线性模型有几百项,那么对于使用者来说也是难以理解的。所以 LIME 只解释决定样本预测结果的 K 个重要特征,非重要特征不予呈现。
- 样本数足够少。LIME 算法是用有代表性的样本来代表总体,使用者通过对有代表性样本的预测结果的解释,来判断模型对这些有代表性样本的预测是否正确,进而判断模型是否正确。如果需要分析的样本过多,无疑会增加使用者的负担,提高理解模型的难度。所以 LIME 通过次模采样,只提供 B 个样本的预测结果的解释,其余样本不予呈现。
由于人类理解能力有限,或者说人脑算力有限,复杂的基因组、转录组、代谢组、蛋白组网络及他们之间的交互网络,即使清晰的呈现在人类面前,人类是否能够加以合理利用?所以我认为,生物组学分析最终必须借用机器的算力来完成。
2. 模型无关(Model-Agnostic)与局部吻合(Local)
LIME 算法可以用于解释任何机器学习算法所构建出的模型,具体算法如下:
- 设待解释的模型为 f,f 的输入为 x,x ∈ Rd
- 设 G 为简单模型集合,简单模型包含线性回归、决策树等,g 为集合 G 中的一个简单模型,在本论文中 g 均为线性模型,设 g 的权重为 wg,有 g(x) = wg · x
- 对样本 xi 构建简单模型 gi,为使 gi 便于理解,gi 的输入不再是 xi,而是 x′i,x′i ∈ {0,1}d′,其中 x → x′ 是通过特定的函数完成的映射。令 gi(x′i) 逼近于 f(xi),从而实现用简单模型 gi 解释任何复杂模型 f 对样本 xi 的预测结果 f(xi)。 由于简单模型 gi 是针对于特定样本 xi 所构建出来的,所以 g 是对 f 特定位点的拟合,即 g 是 f 的局部最优拟合而非全局最优。
- 对 x′i 中非 0 特征随机赋 0,得到新样本 z′i,将 z′i 重新映射为 zi,得到 f(zi),视 〈z′i, zi, f(zi)〉 为对 x′i 和 xi 的一次附近采样,存入集合 Zi 中,如此总共进行 N 次附近采样。
- 以集合 Zi 中 z′i 为自变量,f(zi) 为因变量,用 K-Lasso 算法(详见文末注释)求解 gi 中的 wgi ,算法的伪代码见下图 Algorithm 1。注:K-Lasso 算法有关知识参见 附:K-Lasso 算法简介。

- 设函数 L(f, gi, πxi) = ∑zi∈Z,z′i∈Z′i πxi(zi) ( f(zi) − g(z′i) )2,其中 g(z′i) = wgi · z′i,( f(zi) − g(z′i) )2 表示用 g(z′i) 拟合 f(zi) 的损失 ,πxi (zi) = exp( −D(xi, zi)2 / σ2 ),D(x, z) 为计算 x,z 之间距离的函数,即πx (z) 表示 x,z 之间的距离并作为 ( f(zi) − g(z′i) )2 的权重,表示距离 x 越近的取样 z 所对应的损失越重要,所以函数 L(f, gi, πxi) 表示模型 g 在 xi 处对 f 的拟合效果
- 设函数 ξ(xi) = argmingi∈G L(f, gi, πxi) + Ω(gi),其中 argmingi∈G L(f, gi, πxi) 表示函数 L(f, gi, πxi) 取最小值时 gi 的值。Ω(gi) 表示模型 g 的复杂度(复杂度越高的模型 g 越难以被人所理解),为函数 L 添加了正则化向,若 ‖wgi‖0 > K,Ω(gi) = ∞,若 ‖wgi‖0 ≤ K,Ω(gi) = ‖wgi‖0,其中 ‖wgi‖0 表示 wgi 的 0 范数( 0 范数表示向量中非零元素的个数,即为其稀疏度)。LIME 通过令函数 ξ(xi) 最小,实现 g 在精确度与复杂度之间的平衡。
下图简单展示了 LIME 用简单模型 g 拟合复杂模型 f。复杂黑箱模型 f 由蓝色/粉红色背景表示,可以看出用简单线性模型难以在全局角度很好的拟合 f,所以使用局部拟合。亮红色的十字表示采样 xi,暗红色十字和圆点表示对 xi 进行附近采样得到的样本 zi,构成集合 Zi。十字和圆点大小表示 zi 与 xi 的接近程度 πxi ,用于加权。虚线为通过集合 Zi,运用 K-Lasso 算法 拟合出的简单线性模型 g。

3. 次模采样(Submodular Pick)
LIME 算法是通过对大量样本预测结果的解释,从而判断整体模型的好坏,即通过大量的局部情况反映总体情况。又由于人的理解能力、时间有限,所以要通过尽可能少的样本预测,反映尽可能多的模型情况。论文作者通过次模采样达到上述目的。
次模是指边际效应递减,其中边际效应是指现状态的效益和前一个状态的差值。次模采样是指边际效应递减的采样方法:从空集开始,每次都选择使得边际收益最大的元素加入集合S。Nemhauser 等人证明了次模采样能够达到 (1-1/e) · f(OPT),其中 OPT 表示该问题的最优集合,1-1/e 约为 63%。在本论文中 OPT 表示最能反映模型整体的样本集合。可以看出,次模采样是贪心算法解决 NP-hard 问题的一种应用。
下面说明了 SP-LIME 的具体算法:
- 设模型 f 的训练集为 X,使用者在有限的时间、精力下愿意通过至多 B 个样本的预测结果分析来了解模型 f 的整体预测原理。
- 对 X 中所有样本的预测结果进行 LIME 算法分析,得到 m × d′ 维的权重矩阵 W,其中 m 表示 X 中的样本数量。由上一节对 LIME 算法的描述可知,W 的每行中只有 K 个元素不为 0。
- 设 Ij 表示特征 j 的全局重要性,Ij 2 = ∑i Wij
- 设函数 c(V, W, I) = ∑j 1[∃i∈V:Wij>0]Ij 表示采样得到的样本的特征覆盖度,其中 V 表示从 X 采样得到集合, 1[∃i∈V:Wij>0]Ij 表示:若采样集合 V 里存在样本 xi,其预测结果对应的模型 g 中特征 j 的权重 Wij > 0,有 1 · Ij = Ij,认为 V 中包含特征 j;否则为 0 · Ij = 0,认为 V 中不包含特征 j。
- 通过次模采样,令每次采样使得 c(V∪ {i}, W, I) − c(V, W, I) 最大,直至 V 中样本数等于 B 或 V 覆盖了所有特征时采样结束,得到集合 V。算法伪代码见下图 Algorithm 2。

- 设函数 Pick(W, I) = argmaxV,|V|≤B c(V, W, I),表示希望通过尽可能少的样本(≤ B)覆盖尽可能多的特征,反映尽可能完整的模型时的采样集合 V 所包含的 W、I。
三、LIME 算法效果
1. 对模型预测结果的解释是否准确?
数据集为书评和影评,两个数据集各有 2000 条评论,使用决策树算法(DT)和 L2 正则的线性回归算法(Sparse LR)分别训练模型,这两种算法可以直观反映模型预测时所依据的特征。用 LIME、parzen、greedy、random 四种算法解释模型预测时所依据的特征,并模型真正使用的特征作比较,计算准确率,结果如图 Figure 6、Figure 7。
PS:(i) 所有算法均只使用 10 个特征解释预测结果,即 K = 10;(ii) greedy 算法是指通过逐个移除对原模型预测结果影响最大的特征,直至移除特征达到 10 个;(iii) random 算法是指从总特征中随机挑选 10 个用于解释预测结果;(iiii) 图中纵坐标为 Recall 指解释算法得到的 10 个特征中被真正用于原模型预测的比例的平均值。


在不同数据集合不同算法下,LIME 对结果解释的准确性有一定波动,但都维持在 90% 以上,即 LIME 找到的 10 个特征中有至少 9 个是真实被模型使用的。虽然 90% 的准确率很高,但 需要注意:此例中 LIME 解释的是如线性模型、决策树等简单模型,所以准确率偏高。
上面实验只说明了 LIME 找到的特征与模型 f 预测时使用的特征契合度高,但比重 wij 未必正确。为了说明 wij 正确,即在 f 和 g 中对特定样本的预测结果的贡献相同,作者通过删除某些共有的特征后观察 f 与 g 的预测结果是否同时改变来证明。作者设计了如下实验:在上个实验的基础上,从总特征中随机选择 25% 的特征标记为 “不可靠特征”,其余特征标记为 “可靠特征”,随机选取 “不可靠特征” 的目的是为了让模型 f、g 预测任意样本 xi 时,所用到的特征中都会或多或少的包含一定数量的 “不可靠特征”;然后移除样本 xi 中所有 “不可靠特征”,若移除后模型 f 的预测结果改变,说明样本 xi 中的 “不可靠特征” 对预测结果重要,将样本 xi 标记为 “不可靠样本”,若结果不变,则样本 xi 标记为 “可靠样本”;同理移除 g 中在 f、g 中均出现的 “不可靠特征”,并根据预测结果是否改变对样本 xi 进行标注;计算 xi 在不同模型 f、g 中标签的吻合度,结果见下表 Table 1。注意:由于 greedy 算法导致移除 “不可靠特征” 不会改变预测结果,所以改为出现 “不可靠特征” 即将样本标注为 “不可靠样本”。

从结果可以看出,LIME 解释线性回归(LR)、近邻分类(NN)、随机森林(RF)和支持向量机(SVM)四种算法时生成的简单模型 g 中的权重 W 都是很准确的。虽然 90% 的准确率很高,但 需要注意:此例中 LIME 解释的都是简单模型,所以准确率偏高。
2. 用局部代替总体的效果怎样?
我们知道 SP-LIME 算法是用局部代表总体,所以我们必须了解局部代替总体的效果。如果局部代替总体的效果越好,则通过对不同模型 B 个样本预测结果的解释以找到最优模型的概率就越高。作者通过比较不同方法的采样、解释下,选择最优模型的概率来评判局部代替总体的效果。设计实验如下:
- 将数据集中 1280 条评论作为训练集,320 条评论作为验证集,400 条评论作为测试集。
- 人工生成 10 个噪音特征,向训练集和测试集中 10% 的样本中添加噪音特征,向验证集中 20% 的样本中添加噪音特征。
- 在训练集上用随机森林算法建模,生成多组由 30 棵树构成的随机森林模型,直到找到两组在验证集上预测精度差小于 0.1% 、在测试集上预测精度差大于 5% 的模型,这一对模型无法通过准确率判断模型优劣。
- 从验证集中采样出 B 个样本并查看其预测结果的解释,如果解释中包含噪音特征,则认为此预测结果不可信。选择不可信样本较少的模型作为最优模型,若最优模型在测试集上的预测精度较高,则标记为选择正确。
- 重复步骤 2-4 800 次,计算最优模型选择的正确率,结果见下图 Figure 8。

从结果中可以看出,LIME 的选择正确率始终优于 greedy,次模采样(SP)优于随机采样(random pick,RP),B = 10 时基本达到选择正确率的上限,说明 SP-LIME 算法用局部代替整体效果较好。
3. 是否能够用于提高模型的预测精度?
LIME 算法可以解释模型预测样本结果时所使用的特征,是否可以通过去除模型中使用的无关特征(噪音)而提高模型的预测精度?作者设计实验如下:
- 训练集和待解释模型与 例一 中一致,由于 20 新闻组数据集是有偏的,所以训练得到的模型会使用很多与 “基督教” 和 “无神论” 语义无关的词语(即无关特征)。测试集为作者从 819 个 “基督教” 和 “无神论” 网站中下载的文章。
- 通过 SP-LIME、RP-LIME(K = 10,B = 10)算法将模型的预测原理呈现给受试者,受试者选择出预测结果中与“基督教” 和 “无神论” 语义无关的词语,程序会将这些词语在下一轮训练前从训练集样本中删除。注:受试者均不了解机器学习和特征工程的相关知识。
- 首先将同一模型在不同算法采样下的预测结果解释交给 10 位受试者,受试者根据自己的知识对特征进行筛选。由于不同受试者判断存在差异,所以在第一轮交互后会训练生成 10 个模型。再将这 10 个模型交给 5 位受试者,在第二轮交互后训练生成 50 个模型。最后将 50 个模型再交给这 5 位受试者,在第三轮交互后训练生成 250 个模型。模型在测试集上的预测精度如下图。

图中浅色的线表示 10 个模型在每轮交互后预测精度的均值,如第二轮时表示 5 个模型的精度均值,第三轮时表示 25 个模型的精度均值;深色的线表示模型总预测精度的均值,如第二轮表示 50 个模型的精度均值,第三轮表示 250 个模型的精度均值。从图中可以看出,虽然不同受试者对模型的优化程度存在差异,但总体上模型预测精度都在随着无关特征的筛除而不断上升,其中 SP-LIME 算法尤为明显。说明 SP-LIME 能够用于提高模型的预测精度。
附:K-LASSO 算法简介
Lasso 是 Least Absolute Shrinkage and Selection Operator 的简称,是一种采用了L1正则化(L1-regularization)的线性回归方法。采用了L1正则会使得部分学习到的特征权值为0,从而达到稀疏化和特征选择的目的。
首先,一般的线性回归问题为:给定 n 个样本点 {(x1, y1), (x2, y2), …, (xn, yn)} ,其中 xi ∈ Rd,yi ∈ R,根据观察到的样本点找到一个映射 f:Rd → R,使得误差平方和最小。此时优化目标为:
![[公式]](https://img-blog.csdnimg.cn/2020060211052048.png#pic_center)
其中, β ∈ Rd,β0 ∈ R 是需要优化的系数。一般来说 β0 可以看作是一个偏置 (bias),固定住 β 的值,那么利用一阶导数求最优 β0,得到:
![[公式]](https://img-blog.csdnimg.cn/20200602111527225.png#pic_center)
将得到的结果代入原优化目标得到:
![[公式]](https://img-blog.csdnimg.cn/2020060211190549.png#pic_center)
从上面式子可以看出,假如我们事先对数据进行标准化(中心化),即每个样本数据减去均值,从而得到零均值的数据样本,此时做线性回归就可以不使用偏置。下面假定给定的 n 个样本点是零均值的,即 Σ xi = 0,那么线性回归的优化目标就可以记为:
![[公式]](https://img-blog.csdnimg.cn/20200602112038156.png#pic_center)
上面也可以表示为矩阵形式,记 X = [x1; x2; …; xn]T,这里把每个数据点 xi 当作列向量,则有 X ∈ Rn*d;记 y = (y1, y2, …, yn)T;由于平方和可以写成 L2 范数形式,|| x ||2 = √ Σ xi2,那么矩阵形式的优化目标为:
![[公式]](https://img-blog.csdnimg.cn/20200602113355407.png#pic_center)
一般来说,回归问题是一个函数拟合的过程,我们希望模型不要太复杂,否则很容易发生过拟合现象,所以我们要加入正则化项。不同的正则化项就产生了不同的回归方法,其中以 Ridge Regression (岭回归)和 Lasso最为经典,前者是加入了 L2 正则化项,后者加入的是 L1 正则化项。下面分别给出其优化目标。
Lasso 的优化目标为:

Ridge Regression 的优化目标为:

当我们对正则化项施加限制时,如本论文的 K-Lasso 中要求使用的使用的特征数 ≤ K,即 || β ||1 ≤ K。我们可以将正则化项从目标函数中移除,转变为约束条件。
Lasso 的优化目标变为:
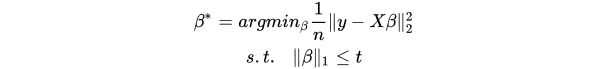
Ridge Regression 的优化目标为:
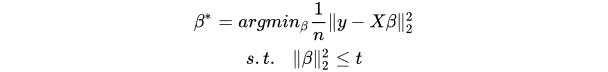
为了说明限制条件与优化目标之间的关系,设 d = 2,有 β = (w1, w2)T。此时 L2 正则化与 L1 正则化的不同见下图。

图中左边解释的是 L1 正则化的几何意义,右边是 L2 正则化。图中椭圆形的彩色线是优化目标关于参数 β = (w1, w2)T 的等高线。假设没有约束条件,那么最小值是椭圆的中心点,但是由于加入了正则化项,相当于是对参数 β 施加了约束,其中左边 L1 正则化将参数限制在一个菱形中,而 L2 正则化则将参数限制在一个圆形区域中。那么从图中可以看出,L1 正则化施加的约束会使得最优值在菱形顶点处取得,即 w1 = 0;而右边L2 正则化项则没有这种倾向。
上面的图从几何意义上解释了 L1 与 L2 正则化的区别,同时这也解释了 L1 与 L2 最大的不同:L1 可以带来稀疏的结果,即 L1 会使得部分参数为零。一方面,可以用来选择特征,一方面可以用来降维压缩数据等等。L1 正则化是和稀疏挂钩,与 L2 正则化挂钩的则是权值衰减(Weight Decay)。简单地说,岭回归倾向于在相关特征之间均匀分布权重,Lasso 则倾向于从相关特征中选取出一个,其余特征权值为零。另外,正则化的目的也可以理解为使模型权重之间的方差较小
上述内容摘自 https://zhuanlan.zhihu.com/p/46999826
有关 Lasso 中参数的解法,也可参见 https://www.cnblogs.com/pinard/p/6018889.html
这篇关于文章:LIME:Why Should I Trust You?的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!