复现国赛数学建模题目解法第一弹——2004年B题：电力市场的输电阻塞管理

python/C++/matlab三选二复现题目解法

国赛历年赛题下载地址：全国大学生数学建模竞赛 (mcm.edu.cn)

一、概括题目要求，写出大致思路

此题题目如下，截取一些关键信息：

整理一下思维导图，大概是这么一个过程 

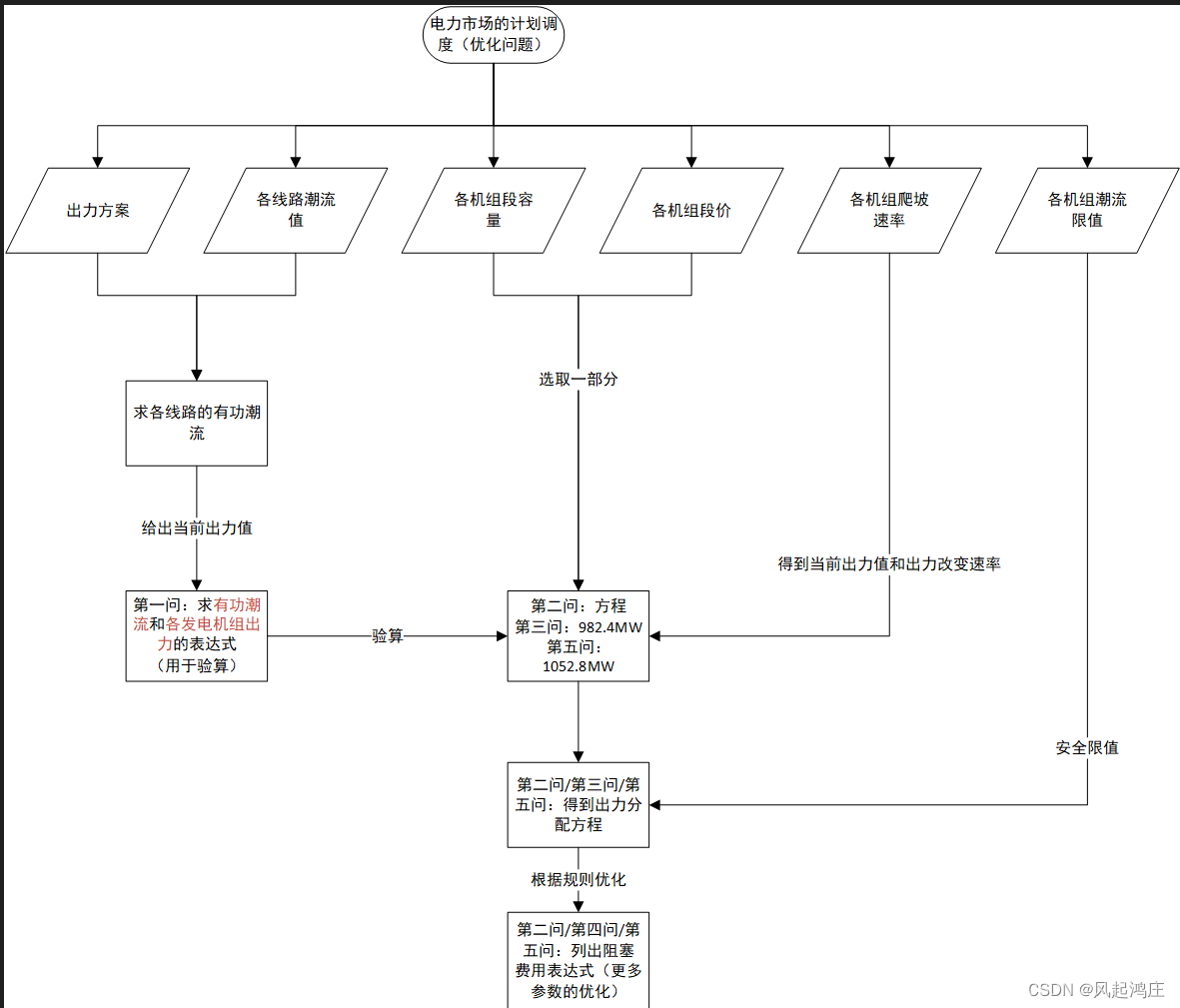
私以为，

其中第一问线性规划

第二问设计全局思路

第三问规划得出方程

第四问单目标规划列表达式

第五问多目标规划

这是一个典型的优化问题，第二问是全局设计的灵魂

二、与相关论文思路进行比对与思路更正

参考了相关的博文和当年的优秀论文，发现自己思考不细致，也有错漏之处，在此进行说明

第一问两篇优秀博文采用的都是多元线性回归的方式，原因是数据太多，没有变量数据，可以直接通过数据拟合方程。

第二问主要就是语言表述，定下解决问题的方案，需要利用费用分摊法，或者是自己建立苏纳法

第三问是单目标规划模型，需要建立两个模型，一个是阻塞费用计算模型，一个是可消除输电阻塞的调整方案的非线性规划模型

第四问我们加入了安全裕度输电的非线性规划模型，给出安全与经济约束下的调整模型，这是一个多目标规划模型

第五问其实是对第三问第四问解法的验证与补充，为此我们需要再建立一个拉闸限电模型，防止用其他模型也找不到输电阻塞的出力分配方案

我们发掘有如下几个难点：

1.八个机组和六个各线路潮流值的关系

2.由段容量确定段价

3.由段价求出清算价

4.读懂输电阻塞规则

三、复现论文解法

matlab版：

第一问：多元线性回归

所谓多元线性回归，其实就是数据拟合之后进行统计分析。我们需要找到表一和表二数据之间的关系，因为是要求有功潮流对各发电机组出力的表达式，我们可以列6个式子，其中每个式子具有8个参数。这里我们采用regress()进行拟合。

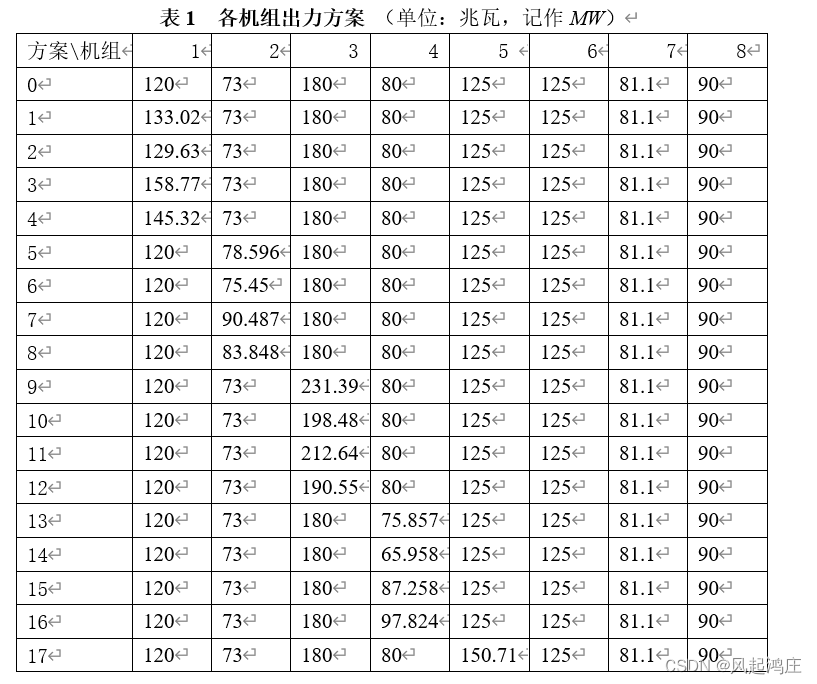
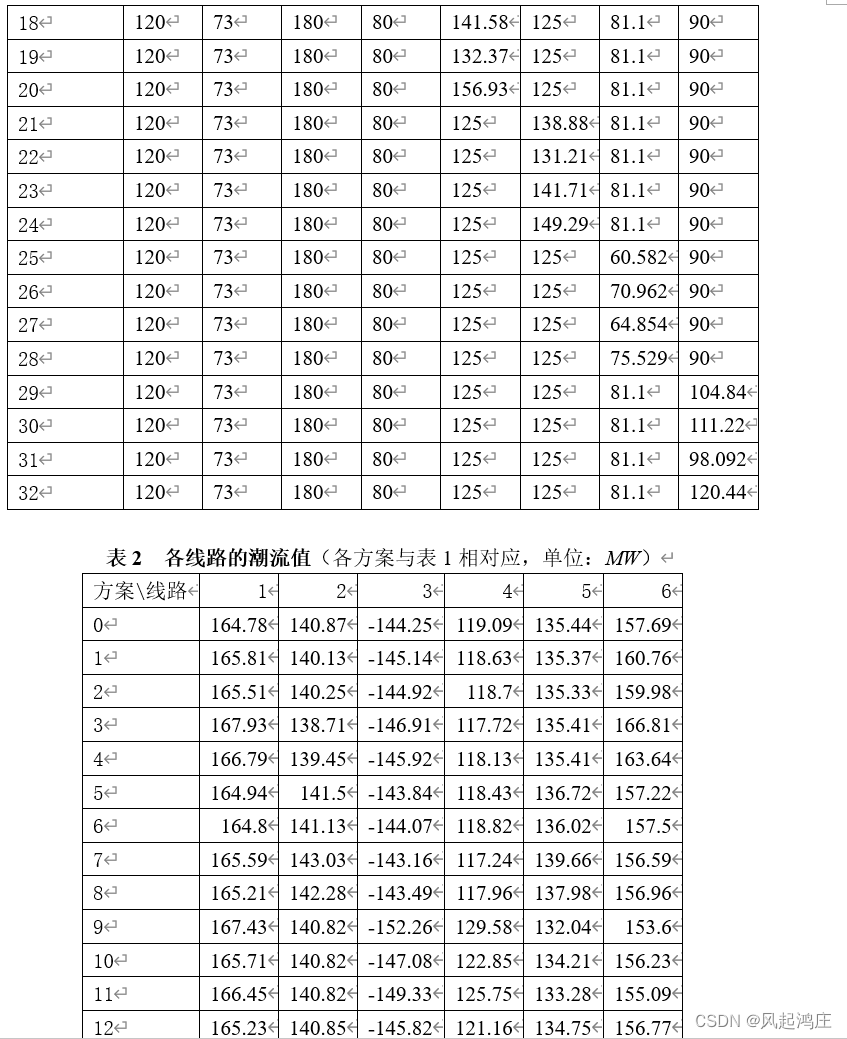
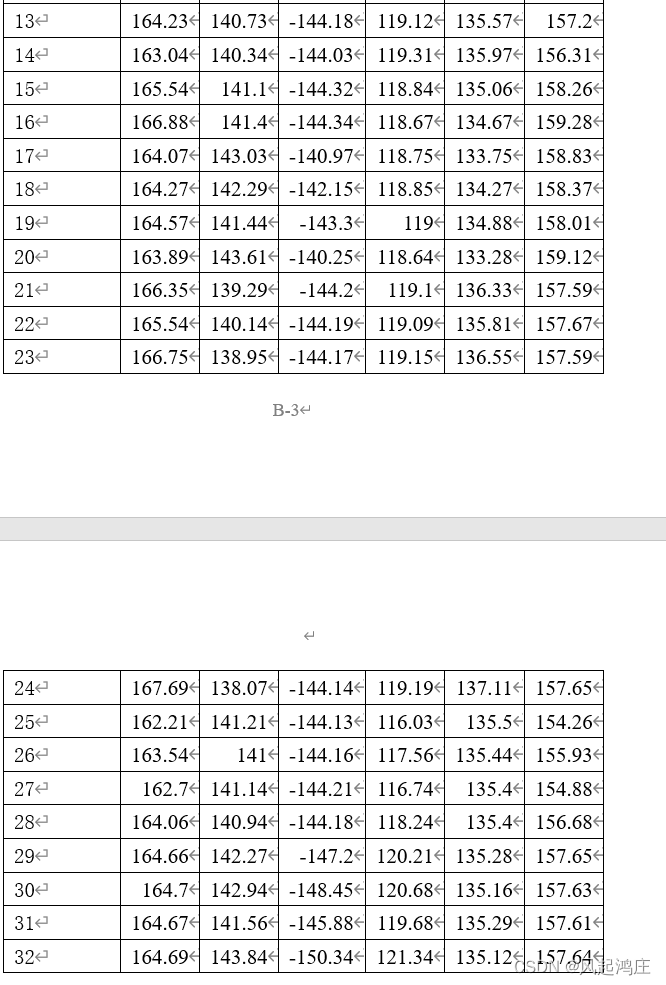
可以看出我们两个表格都是有32个方案，方案0属于对照组，可以用它来进行验证。

我们可以把两个表格合在一起分析。y是各线路的有功潮流值，x1到x8代表8个机组，系数由这32个方案决定。下面的代码是算y1时列的，其他同理。

clc;
clear all;
data1=xlsread('2004_b1.xlsx');
x1=xlsread('2004_b1.xlsx','B3:B34');
x2=xlsread('2004_b1.xlsx','C3:C34');
x3=xlsread('2004_b1.xlsx','D3:D34');
x4=xlsread('2004_b1.xlsx','E3:E34');
x5=xlsread('2004_b1.xlsx','F3:F34');
x6=xlsread('2004_b1.xlsx','G3:G34');
x7=xlsread('2004_b1.xlsx','H3:H34');
x8=xlsread('2004_b1.xlsx','I3:I34');
y=xlsread('2004_b2.xlsx','B3:B34');
%在这里各个机组之间其实是互不影响的，所以没必要计算具有交互效应项的线性模型的回归系数（向量点乘），这里列下式子不予运行
%X1=[ones(size(x1)) x1 x2 x1.*x2];
%X2=[ones(size(x3)) x3 x4 x3.*x4];
%X3=[ones(size(x5)) x5 x6 x5.*x6];
%X4=[ones(size(x5)) x7 x8 x7.*x8];
%但各个方案之间是影响的，所以要计算它们之间的回归系数
X1=[ones(32,1),x1];
X2=[ones(32,1),x2];
X3=[ones(32,1),x3];
X4=[ones(32,1),x4];
X5=[ones(32,1),x5];
X6=[ones(32,1),x6];
X7=[ones(32,1),x7];
X8=[ones(32,1),x8];
b1=regress(y,X1);
b2=regress(y,X2);
b3=regress(y,X3);
b4=regress(y,X4);
b5=regress(y,X5);
b6=regress(y,X6);
b7=regress(y,X7);
b8=regress(y,X8);
b_1=[b1(1)+b2(1)+b3(1)+b4(1)+b5(1)+b6(1)+b7(1)+b8(1)]/8
x1fit = min(x1):32:max(x1);
x2fit = min(x2):32:max(x2);
x3fit = min(x3):32:max(x3);
x4fit = min(x4):32:max(x4);
x5fit = min(x5):32:max(x5);
x6fit = min(x6):32:max(x6);
x7fit = min(x7):32:max(x7);
x8fit = min(x8):32:max(x8);
YFIT = b_1 + b1(2)*x1fit + b2(2)*x2fit +b3(2)*x3fit + b4(2)*x4fit+b5(2)*x5fit + b6(2)*x6fit +b7(2)*x7fit + b8(2)*x8fit

算出的拟合式子为：

 另外四个式子也是这么列出来的

我发现算出的结果其实比方案0的值大，比如说方案0中，线路1的值是160，但我们算出来的总结果是200。对照示例论文中的式子发现是b_1值偏差比较大，但我也没想到解决方式，因为理应来说b1(1)到b8(1)的值都比120大，但我发现示例论文的b_1值居然才110多，所以一直没想懂哪出现了问题，欢迎评论区指正

算出的结果与方案0结果比较：

方案0：

算出的结果:

之后还会补充文章继续复现，敬请期待