算法与数据结构：AOE网与关键路径

前言

这次来介绍一下AOE网和关键路径，应该在工程等领域应用的很多。

什么是AOE网？

不要搞混了，这次说的不是AOV网（activity on vertex），而是AOE网（activity on edge）。顾名思义，这个新东西的【边】占的重要性要更多一些，AOE网是一个【带权】有向图，主要描述现实世界的工程预计进度。其中顶点表示事件，有向边表示活动的过程，而边上的权一般表示活动所用的时间。

同时，AOE网还有两个特殊的顶点，就是有一个入度为0的顶点（源点）表示开始事件（比如开工仪式）；一个出度为0的顶点（汇点）表示工程结束事件。

什么是关键路径？

说起AOE网和工程，就必须要提一下【关键路径】了。关键路径是从源点到汇点的【最长】路径。而关键路径上的活动被称为“关键活动”。

注意，由于可能出现两种路径有相同的长度，所以关键路径可能【不唯一】。

关键路径演示如下：

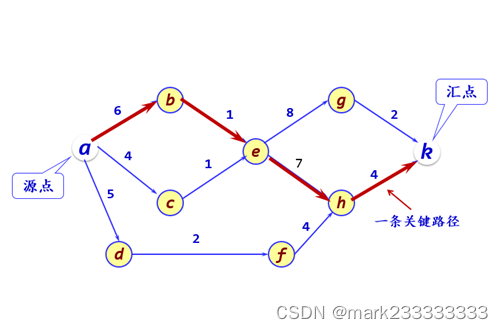
算法与应用

在实际工程应用时，我们通常会解决两个问题：

1 . 估算整个工程需要多少时间。

2 . 判断哪些活动是关键活动，如何确定关键路径？

对于如何确定关键路径这个问题，我们需要清楚四个问题：

【事件】的最早发生时间、最迟发生时间 和 【活动】的最早发生时间、最迟发生时间。

1.【事件】的最早发生时间

如果求事件的最早开始时间：方便起见，我们可以规定源点事件的最早开始时间为0。对于其他点（v），那么事件v的最早发生时间是从【源点】到v的最大路径长度。

定义图中任一事件vi的最早开始时间ve(i)如下：

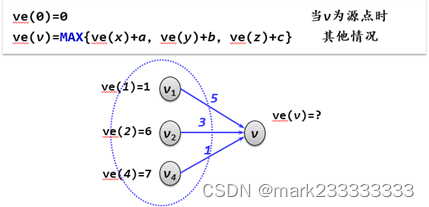
注：源点不用多说。对于其他点v，前面【所有】的事儿（v的前驱节点的最早发生时间加活动的时间）办完了，它才能开始。也就是前面最晚的事儿办完的这一刻，然后它刚好开始，就是v最早的时间了。

2.【事件】的最迟发生时间

定义图中任一事件vi的最迟开始时间vl(i)如下：（不影响整个工程进度的情况下，v发生的最晚时间）

 

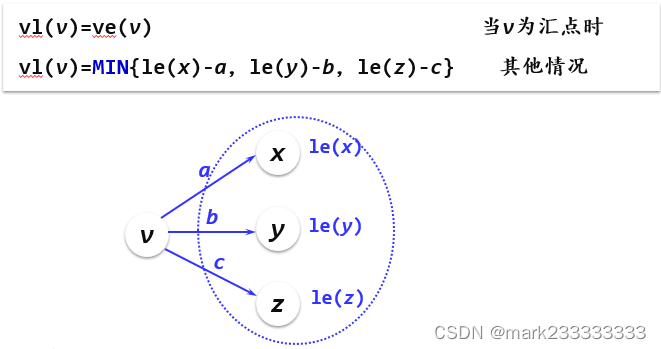
注：要注意汇点最迟发生时间正是【最早】发生时间，对于其他点v，也就是后面紧接活动时刻的最小值。（如果v的发生时间大于这个最小值，意味着后面的活动也要推迟。递归来讲，完工时期也要推迟，也就是【影响】了总工期）

3.【活动】的最早、最迟开始时间

定义：

活动ai的最早开始时间e(i)指该活动起点事件vj的最早开始事件。（e(i)=ve(j)）

活动ai的最迟开始时间l(i)指活动的终点事件vk的最迟开始时间【减去】ai的持续时间wjk。

4.关键路径与关键活动

对于每个活动a，求出d(a)=l(a)-e(a)，若d(a)为0，则称活动a为关键活动。

说到这里，可能很多同学要问了：为什么按照这个法子求出的活动就是关键活动呢？

其实，对于每个AOE网来说，关键路径的意义也在于整个工程的最早完成时间。

我们的第一步就是先求了每个事件的最早发生时间。

那么又一个问题来了：每个AOE网一定有它的关键路径吗？其实是的，不妨先看一下汇点vn（结束事件），它的的前驱节点里【至少】有一个点vi，vi的最早开始时间加上后接边权值都等于汇点的【最早开始时间】（也就是都等于【最大值】）。那么取满足条件的vi，，它的前驱节点里【至少】有一个点va，va的最早开始时间加上后接边的权值达到了vi的【最早开始时间】（也就是都等于【最大值】）。再取满足条件的va，做同样操作，递归到源点。所以“v0 … va, vi, vn”加上其边就可以被当作一条关键路径。

显而易见，可以这么被推下来的路径（一步紧接一步，总路径长就为活动总时间）都是关键路径；反之亦然（关键路径的若在这种情况可以不是一步接一步，则允许缩短其路径长即工期，与原来假设工期最短矛盾）。

也就是说，关键路径的充要条件为其关键活动是一步紧接一步的（工程结束时间为最早时），即活动最迟开始时间必须等于最早开始时间。

最后，把满足条件的关键活动连接起来，就构造出关键路径了。