本文主要是介绍第 4 章 数据的概括性度量,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
重点及知识点总结:
众数:可能无众数,一个众数,多个众数。
中位数:排完序,若是偶数个则需要将中间两个数相加除以2,而不是向上取整。
四分位数:排序后出于25%和75%的数,分别叫做下分位数和上分位数。
平均数:也叫做均值。
加权平均数:一般用于分组数据。
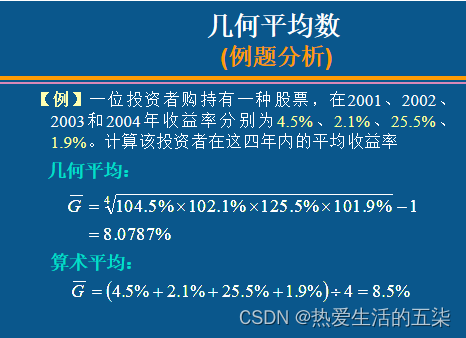
几何平均数:主要用于计算平均增长率,是n个变量值乘积的n次方根。
左偏分布:数据小的值多。右偏分布:数据大的值比较多。
异众比率:不是众数的频数占总频数的比例。如总数个数占30%,则异众比率则是1-30% = 70%。
极差:一组数据的最大值和最小值之差。
平均差:各变量值于平均数的差 的绝对值的平均数。平均差一般不用,性质不好。
方差和标准差:是重点。注意对于样本差和方差,分母对应总体是n,样本是n-1。注意分组数据的公式有点变化。
样本标准差为12.58,样本标准差的含义是:每一天的销售量与平均数相比,平均相差21.58台。
自由度:自由度是指一组数据中可以自由取值的个数。按着这一逻辑,如果对n个观测值附加的约束个数为k个,自由度则为n-k。
标准分数:
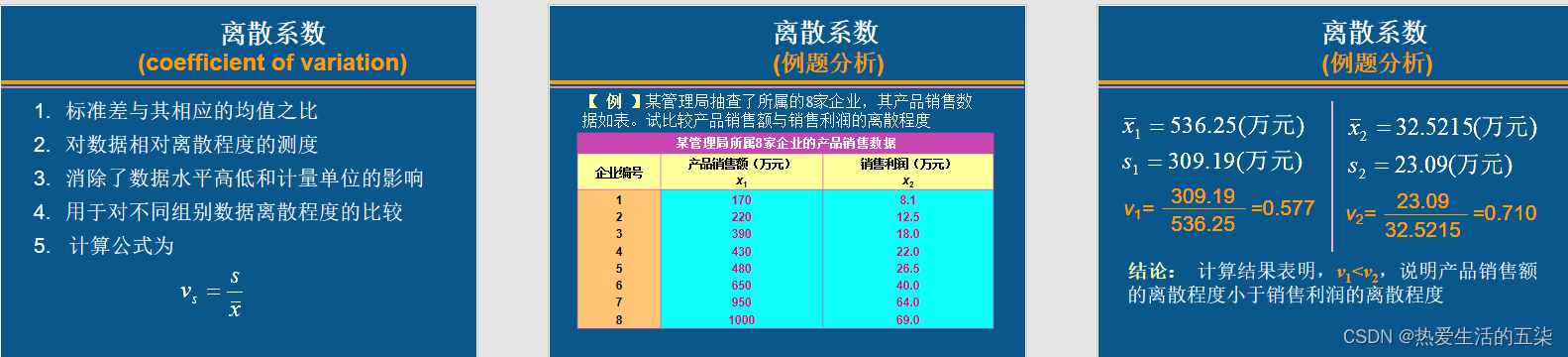
离散系数:标准差与其相应的均值之比v=s/x拔
经验法则:对称分布,平均数加减标准差分别对应概率。
对称分布的经验法则,123标准差对应68%,95%,99%。
切比雪夫不等式:非对称分布,2,3,4标准差对应75%,89%,94%。
具体内容:
4.1集中趋势的度量









平均收益率要用几何平均数来算,不能用平均数来算:

4.2离散趋势的度量
异众比率:不是众数的频数占总频数的比例。如总数个数占30%,则异众比率则是1-30% = 70%。
极差:一组数据的最大值和最小值之差。
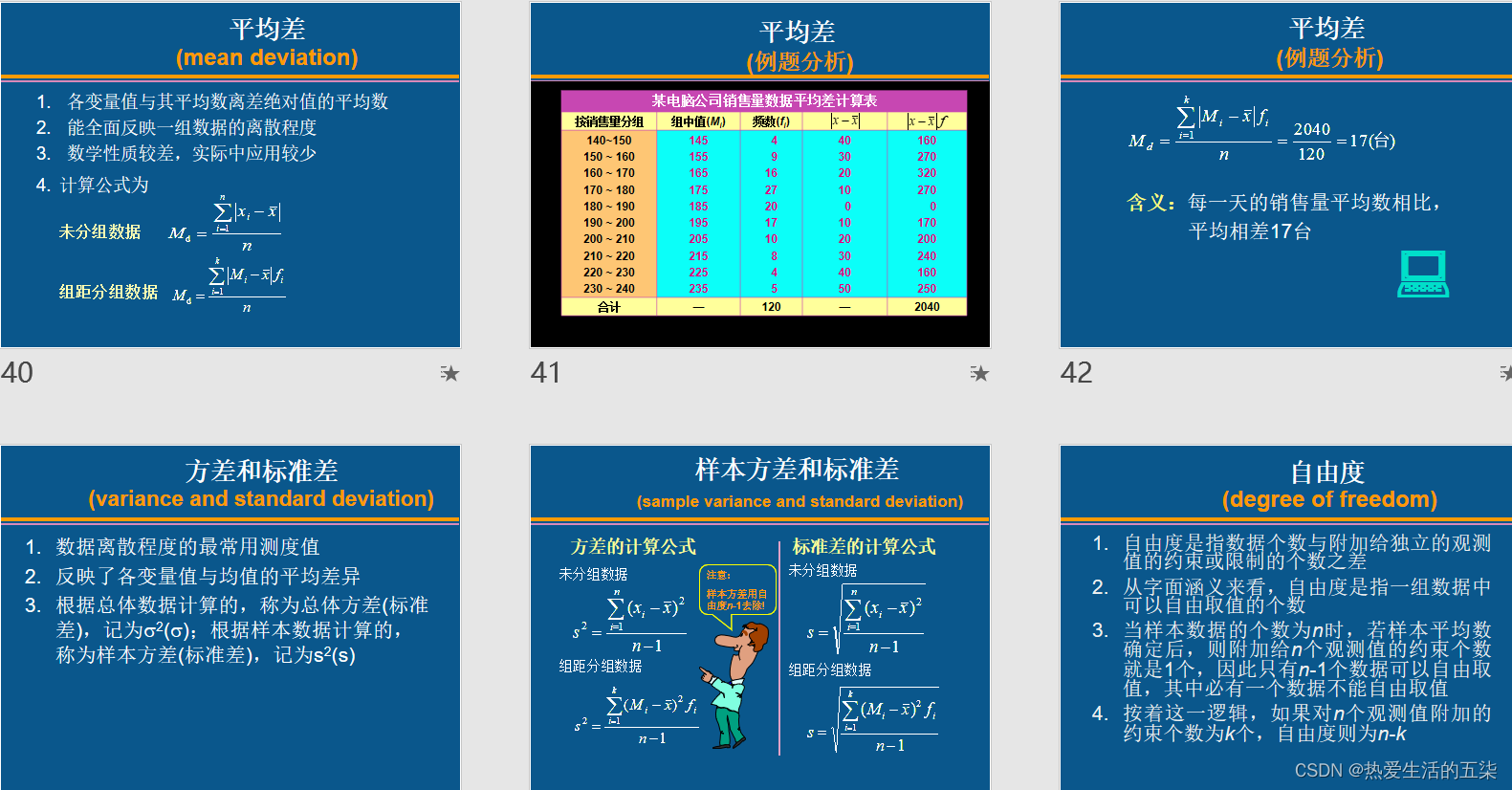
平均差:各变量值于平均数的差 的绝对值的平均数。平均差一般不用,性质不好。
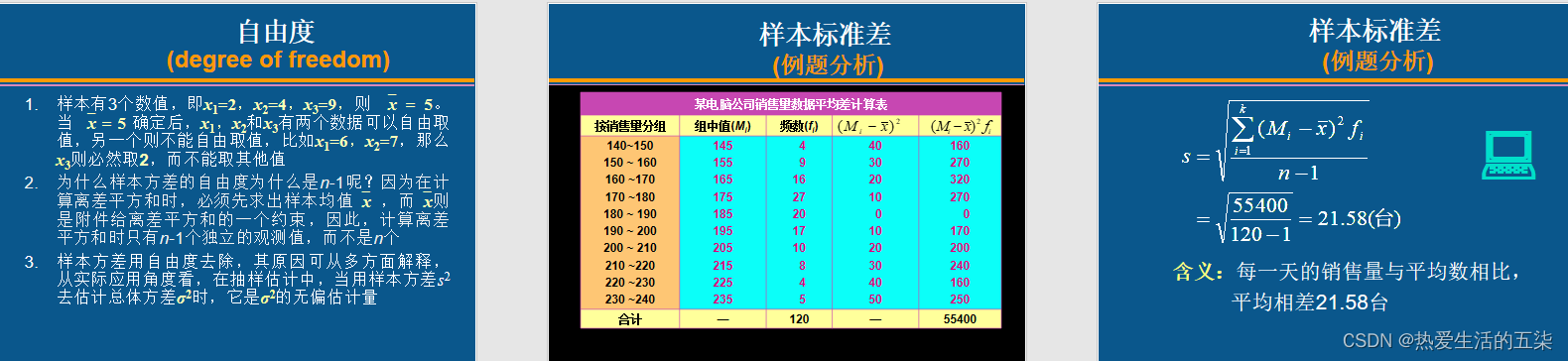
方差和标准差:是重点。注意对于样本差和方差,分母对应总体是n,样本是n-1。注意分组数据的公式有点变化。
样本标准差为12.58,样本标准差的含义是:每一天的销售量与平均数相比,平均相差21.58台。
自由度:自由度是指一组数据中可以自由取值的个数。按着这一逻辑,如果对n个观测值附加的约束个数为k个,自由度则为n-k。







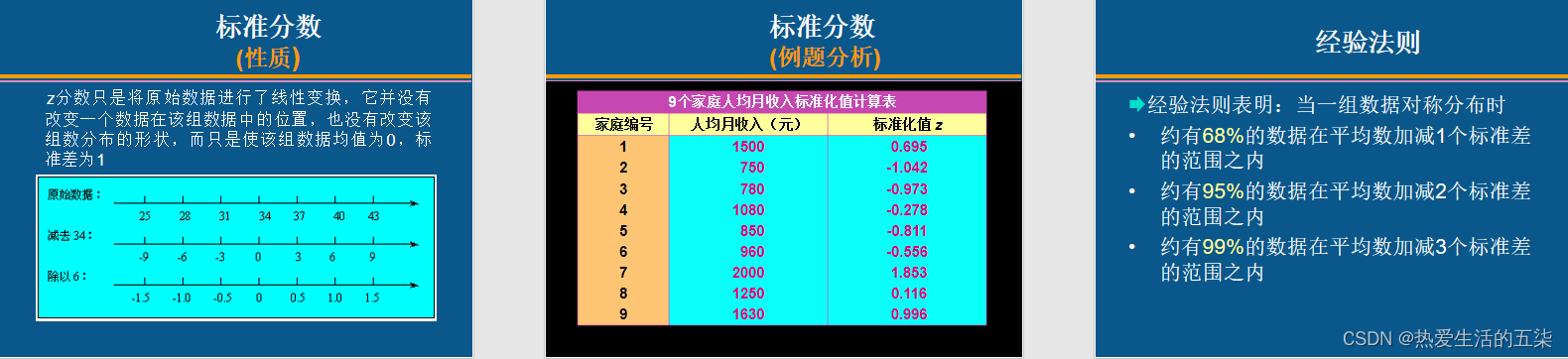

离散系数:标准差与其相应的均值之比v=s/x拔
经验法则:对称分布,平均数加减标准差分别对应概率。
切比雪夫不等式:非对称分布,2,3,4标准差对应75%,89%,94%。
这篇关于第 4 章 数据的概括性度量的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




