本文主要是介绍惯性导航学习过程记录(旋转矩阵部分),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
坐标系变换经常弄混淆,这里记录一下相关旋转的过程,代码是CSDN上下的,链接找不到了,直接搜索惯性导航程序,然后随便买一个就行了,程序大家写的都差不多。
最近从CSDN上下载的MATLAB程序都会出现中文显示乱码问题,解决方法:用记事本打开.m文件,重新另存为,格式改成ANSI,然后回到matlab里面就能打开了。

1.绕单轴旋转
1.1 绕x轴旋转
function angleInRadians = deg2rad(angleInDegrees)
% 将角度从度转换为弧度。
% DEG2RAD(X) converts angle units from degrees to radians for each
% element of X.
%
% See also RAD2DEG.% Copyright 2015 The MathWorks, Inc.if isfloat(angleInDegrees)angleInRadians = (pi/180) * angleInDegrees;
elseerror(message('MATLAB:deg2rad:nonFloatInput'))
endfunction Cb2n = ch_rotx(theta)
% 3D初等旋转, theta为旋转角度,rad
Cb2n = [1 0 0; 0 cos(theta) -sin(theta); 0 sin(theta) cos(theta)];
endtheta = deg2rad(30);
Cb2nX = ch_rotx(theta);
fprintf("b系到n系,绕X轴旋转%.3f ° 的旋转矩阵 Cb2nX 为\n", rad2deg(theta));
Cb2nX
运行结果:
b系到n系,绕X轴旋转30.000 ° 的旋转矩阵 Cb2nX 为
Cb2nX =
1.0000 0 0
0 0.8660 -0.5000
0 0.5000 0.8660
1.2 绕y轴旋转
function Cb2n = ch_roty(theta)
% 3D鍒濈瓑鏃嬭浆锛� theta涓烘棆杞搴︼紝rad
Cb2n = [cos(theta), 0 sin(theta); 0 1 0; -sin(theta) 0 cos(theta)];
endtheta = deg2rad(40);
Cb2nY = ch_roty(theta);
fprintf("b系到n系的,绕Y轴旋转%.3f ° 的旋转矩阵 Cb2nX为\n", rad2deg(theta));
Cb2nY运行结果:
b系到n系的,绕Y轴旋转40.000 ° 的旋转矩阵 Cb2nX为
Cb2nY =
0.7660 0 0.6428
0 1.0000 0
-0.6428 0 0.7660
1.3 绕z轴旋转
function Cb2n = ch_rotz(theta)
% 3D鍒濈瓑鏃嬭浆锛� theta涓烘棆杞搴︼紝rad
Cb2n = [cos(theta) -sin(theta) 0; sin(theta) cos(theta) 0; 0 0 1];
endtheta = deg2rad(50);
Cb2nZ = ch_rotz(theta);
fprintf("b系到n系的,绕Z轴旋转%.3f ° 的旋转矩阵 Cb2nX为\n", rad2deg(theta));
Cb2nZ
运行结果:
b系到n系的,绕Z轴旋转50.000 ° 的旋转矩阵 Cb2nX为
Cb2nZ =
0.6428 -0.7660 0
0.7660 0.6428 0
0 0 1.000
1.4 利用旋转矩阵对一点进行旋转
Ab = [0 0 1]';
fprintf("b系下有点 A:%.3f %.3f %.3f\n", Ab(1), Ab(2), Ab(3));An = Cb2nX*Ab;
fprintf("b系下点A经过Cb2nX旋转到n系为: %.3f %.3f %.3f\n",An(1), An(2), An(3));An = Cb2nY*Ab;
fprintf("b系下点A经过Cb2nY旋转到n系为: %.3f %.3f %.3f\n",An(1), An(2), An(3));An = Cb2nZ*Ab;
fprintf("b系下点A经过Cb2nZ旋转到n系为: %.3f %.3f %.3f\n",An(1), An(2), An(3));运行结果:
b系下有点 A:0.000 0.000 1.000
b系下点A经过Cb2nX旋转到n系为: 0.000 -0.500 0.866
b系下点A经过Cb2nY旋转到n系为: 0.643 0.000 0.766
b系下点A经过Cb2nZ旋转到n系为: 0.000 0.000 1.000
上述重点:
- 角度需要先经过函数 deg2rad ()化成弧度
- 旋转过程为旋转矩阵*b系下一点的坐标
- 旋转矩阵尺寸是3x3,因此b系下的点坐标为3行1列的格式
2.绕多个轴旋转
2.1 312旋转方式
先绕z轴旋转50度,再绕x轴旋转30度,最后绕y轴旋转40度,也就是312
eul = [30 40 50]';fprintf("按312顺序(先转Z-然后X-最后Y)旋转,其中X,Y,Z旋转角度为%d° %d° %d° 得到对应的坐标变换矩阵:\n", eul(1), eul(2), eul(3));eul_rad = deg2rad(eul);
Cb2n_312 = ch_rotz(eul_rad(3)) * ch_rotx(eul_rad(1)) * ch_roty(eul_rad(2));
Cb2n_312
运行结果:
按312顺序(先转Z-然后X-最后Y)旋转,其中X,Y,Z旋转角度为30° 40° 50° 得到对应的坐标变换矩阵:
Cb2n_312 =
0.2462 -0.6634 0.7066
0.7934 0.5567 0.2462
-0.5567 0.5000 0.6634
2.2 321旋转方式
fprintf("按321顺序(先转Z-然后Y-最后Z)旋转,其中X,Y,Z旋转角度为%d° %d° %d° 得到对应的坐标变换矩阵:\n", eul(1), eul(2), eul(3));Cb2n_321 = ch_rotz(eul_rad(3)) * ch_roty(eul_rad(2)) * ch_rotx(eul_rad(1));
Cb2n_321运行结果:
按321顺序(先转Z-然后Y-最后Z)旋转,其中X,Y,Z旋转角度为30° 40° 50° 得到对应的坐标变换矩阵:
Cb2n_321 =
0.4924 -0.4568 0.7408
0.5868 0.8029 0.1050
-0.6428 0.3830 0.6634
旋转方式不同得到的旋转矩阵也不相同!
2.3 b系转n系-n系转b系
fprintf("从n系到b系的坐标变换矩阵Cn2b:(既Cb2n的转置)\n");
Cn2b_312 = Cb2n_312';
Cn2b_312运行结果:
从n系到b系的坐标变换矩阵Cn2b:(既Cb2n的转置)
Cn2b_312 =
0.2462 0.7934 -0.5567
-0.6634 0.5567 0.5000
0.7066 0.2462 0.6634
n转到b,是Cn2b,注意角标,n to b
2.4 欧拉角反求Cn2b
fprintf("Cn2b也可以通过欧拉角计算:, 注意矩阵的旋转顺序 和 欧拉角 符号都要变\n");
Cn2b_312 = ch_roty(-eul_rad(2)) * ch_rotx(-eul_rad(1)) * ch_rotz(-eul_rad(3));
Cn2b_312
运行结果:
Cn2b也可以通过欧拉角计算:, 注意矩阵的旋转顺序 和 欧拉角 符号都要变
Cn2b_312 =
0.2462 0.7934 -0.5567
-0.6634 0.5567 0.5000
0.7066 0.2462 0.6634
快捷记法:312 倒过来 - 213
3. 从姿态角 pitch, roll, yaw 到旋转矩阵
pitch,roll,yaw绕哪一个轴并不固定,每个地方的习惯不同
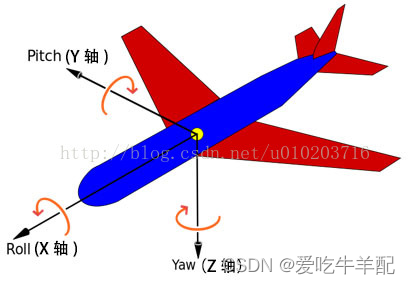
pitch - 俯仰角 - 绕y轴
roll - 横滚角 - 绕x轴
yaw - 航向角 - 绕z轴(有的地方也写heading)
3.1 pitch 是x轴的情况,312
function [Cb2n_312, Cb2n_321] = ch_eul2m(att)
% 将欧拉角转换为姿态阵
% 复用严龚敏老师的a2mat
%
% Input: att 单位:rad
% 对于312((Z->X->Y))顺序,对应att = [pitch(绕X轴) roll(绕Y轴) yaw(绕Z轴)]
% 对于321(Z->Y->X)顺序,对应att = [roll(绕X轴) pitch(绕Y轴) yaw(绕Z轴)]
% Outputs:
% Cb2n_312: 312欧拉角顺序下转换后的Cb2n
% Cb2n_321: 321欧拉角顺序下转换后的Cb2ns = sin(att); c = cos(att);si = s(1); sj = s(2); sk = s(3); ci = c(1); cj = c(2); ck = c(3);Cb2n_312 = [ cj*ck-si*sj*sk, -ci*sk, sj*ck+si*cj*sk;cj*sk+si*sj*ck, ci*ck, sj*sk-si*cj*ck;-ci*sj, si, ci*cj ];if nargout==2 % dual Euler angle DCMCb2n_321 = [ cj*ck, si*sj*ck-ci*sk, ci*sj*ck+si*sk;cj*sk, si*sj*sk+ci*ck, ci*sj*sk-si*ck;-sj, si*cj, ci*cj ];endfunction [eul_312, eul_321] = ch_m2eul(Cb2n)
% 将姿态阵转为欧拉角
% 复用严龚敏老师的m2att
%
% Input: 姿态阵Cb2n: b系->n系的坐标变换矩阵
% Outputs:
% eul_312: 312(Z->X->Y)旋转顺序下的欧拉角: att = [pitch(绕X轴) roll(绕Y轴) yaw(绕Z轴)]
% eul_321: 321(Z->Y->X)旋转顺序下的欧拉角: att = [roll(绕X轴) pitch(绕Y轴) yaw(绕Z轴)]eul_312 = [ asin(Cb2n(3,2));atan2(-Cb2n(3,1),Cb2n(3,3)); atan2(-Cb2n(1,2),Cb2n(2,2)) ];if nargout==2 % dual Euler angleseul_321 = [ atan2(Cb2n(3,2),Cb2n(3,3)); asin(-Cb2n(3,1)); atan2(Cb2n(2,1),Cb2n(1,1)) ];endeul_312 = [30, 40, 50]; % [pitch(绕X轴) roll(绕Y轴) yaw(绕Z轴)]fprintf("按312顺序(先转Z-然后X-最后Y)旋转,其中X,Y,Z旋转角度为%.3f° %.3f° %.3f° 得到对应的坐标变换矩阵:\n", eul_312(1), eul_312(2), eul_312(3));eul_312rad = deg2rad(eul_312);
[Cb2n_312, ~] = ch_eul2m(eul_312rad);
Cb2n_312
运行结果:
按312顺序(先转Z-然后X-最后Y)旋转,其中X,Y,Z旋转角度为30.000° 40.000° 50.000° 得到对应的坐标变换矩阵:
Cb2n_312 =
0.2462 -0.6634 0.7066
0.7934 0.5567 0.2462
-0.5567 0.5000 0.6634将Cb2n_312转回欧拉角:
坐标变换矩阵转欧拉角:30.000°(Pitch) 40.000°(Roll) 50.000°(Yaw)
3.2 roll 是x轴的情况,321
eul_321 = [30, 40, 50]; % [roll(绕X轴) pitch(绕Y轴) yaw(绕Z轴)]fprintf("\n按321顺序(先转Z-然后Y-最后X)旋转,其中X,Y,Z旋转角度为%.3f° %.3f° %.3f° 得到对应的坐标变换矩阵:\n", eul_321(1), eul_321(2), eul_321(3));eul_321rad = deg2rad(eul_321);
[~, Cb2n_321] = ch_eul2m(eul_321rad);
Cb2n_321fprintf("将Cb2n_321转回欧拉角:\n");
[~, eul_321] = ch_m2eul(Cb2n_321);
eul_321 = rad2deg(eul_321);fprintf("坐标变换矩阵转欧拉角:%.3f°(Roll) %.3f°(Pitch) %.3f°(Yaw)\n", eul_321(1), eul_321(2), eul_321(3));
运行结果:
按321顺序(先转Z-然后Y-最后X)旋转,其中X,Y,Z旋转角度为30.000° 40.000° 50.000° 得到对应的坐标变换矩阵:Cb2n_321 =
0.4924 -0.4568 0.7408
0.5868 0.8029 0.1050
-0.6428 0.3830 0.6634将Cb2n_321转回欧拉角:
坐标变换矩阵转欧拉角:30.000°(Roll) 40.000°(Pitch) 50.000°(Yaw)
反正就是旋转顺序永远是,yaw ,pitch,roll
4. 四元数与等效旋转矢量
4.1 利用旋转矩阵实现向量的不同坐标系转化
function q = ch_qmul(q1, q2)
% 四元数相乘
%
% Inputs: Q1 Q2, 四元数和矩阵一样,不满足交换律
% Outputs: Q
% q = [ q1(1) * q2(1) - q1(2) * q2(2) - q1(3) * q2(3) - q1(4) * q2(4);q1(1) * q2(2) + q1(2) * q2(1) + q1(3) * q2(4) - q1(4) * q2(3);q1(1) * q2(3) + q1(3) * q2(1) + q1(4) * q2(2) - q1(2) * q2(4);q1(1) * q2(4) + q1(4) * q2(1) + q1(2) * q2(3) - q1(3) * q2(2) ];function Qb2n = ch_m2q(Cb2n)
% 姿态阵转四元数
%
% Input: Cb2n
% Output: Qb2n
%C11 = Cb2n(1,1); C12 = Cb2n(1,2); C13 = Cb2n(1,3); C21 = Cb2n(2,1); C22 = Cb2n(2,2); C23 = Cb2n(2,3); C31 = Cb2n(3,1); C32 = Cb2n(3,2); C33 = Cb2n(3,3); if C11>=C22+C33q1 = 0.5*sqrt(1+C11-C22-C33);q0 = (C32-C23)/(4*q1); q2 = (C12+C21)/(4*q1); q3 = (C13+C31)/(4*q1);elseif C22>=C11+C33q2 = 0.5*sqrt(1-C11+C22-C33);q0 = (C13-C31)/(4*q2); q1 = (C12+C21)/(4*q2); q3 = (C23+C32)/(4*q2);elseif C33>=C11+C22q3 = 0.5*sqrt(1-C11-C22+C33);q0 = (C21-C12)/(4*q3); q1 = (C13+C31)/(4*q3); q2 = (C23+C32)/(4*q3);elseq0 = 0.5*sqrt(1+C11+C22+C33);q1 = (C32-C23)/(4*q0); q2 = (C13-C31)/(4*q0); q3 = (C21-C12)/(4*q0);endQb2n = [q0; q1; q2; q3];function Cb2n = ch_q2m(Qb2n)
% 四元数转姿态阵
%
% Input: Qb2n
% Output: Cb2n
%q11 = Qb2n(1)*Qb2n(1); q12 = Qb2n(1)*Qb2n(2); q13 = Qb2n(1)*Qb2n(3); q14 = Qb2n(1)*Qb2n(4); q22 = Qb2n(2)*Qb2n(2); q23 = Qb2n(2)*Qb2n(3); q24 = Qb2n(2)*Qb2n(4); q33 = Qb2n(3)*Qb2n(3); q34 = Qb2n(3)*Qb2n(4); q44 = Qb2n(4)*Qb2n(4);Cb2n = [ q11+q22-q33-q44, 2*(q23-q14), 2*(q24+q13);2*(q23+q14), q11-q22+q33-q44, 2*(q34-q12);2*(q24-q13), 2*(q34+q12), q11-q22-q33+q44 ];function qout = ch_qconj(qin)
qout = [qin(1); -qin(2:4)];function vo = ch_qmulv(q, vi)
% 向量通过四元数做3D旋转
%
% Inputs: q - Qb2n
% vi - 需要旋转的向量
% Output: vout - output vector, such that vout = q*vin*conjugation(q)
%
% See also q2mat, qconj, qmul.% qi = [0; vi];
% qo = ch_qmul(ch_qmul(q,qi),ch_qconj(q));
% vo = qo(2:4,1);qo1 = - q(2) * vi(1) - q(3) * vi(2) - q(4) * vi(3);qo2 = q(1) * vi(1) + q(3) * vi(3) - q(4) * vi(2);qo3 = q(1) * vi(2) + q(4) * vi(1) - q(2) * vi(3);qo4 = q(1) * vi(3) + q(2) * vi(2) - q(3) * vi(1);vo = vi;vo(1) = -qo1 * q(2) + qo2 * q(1) - qo3 * q(4) + qo4 * q(3);vo(2) = -qo1 * q(3) + qo3 * q(1) - qo4 * q(2) + qo2 * q(4);vo(3) = -qo1 * q(4) + qo4 * q(1) - qo2 * q(3) + qo3 * q(2);
clear;
clc
close all;%% 已知
Vn = [0 0 1];
Qa2n = [0.981 0.010 -0.191 0.011]'; % a系转到n系的四元数
Qb2n = [0.936 -0.259 -0.233 -0.046]'; % b系转到n系的四元数Va = [0.375 0.021 0.876]'; % a 系上的一点
Vb = [0.465 -0.447 0.712]'; % b 系上的一点%% 四元数转成矩阵
Ca2n = ch_q2m(Qa2n); % a系转到n系的旋转矩阵
Cb2n = ch_q2m(Qb2n); % b系转到n系的旋转矩阵%%计算 Ca2b, Qa2b
Ca2b = Cb2n' * Ca2n; % a系 转到 b系 = 先 a系到 n系,然后n 系到b系(用b系转到n系的旋转矩阵的转置求)
Qa2b = ch_m2q(Ca2b);%% 转换并显示结果
fprintf("a2b的四元数为:%.3f %.3f %.3f %.3f\n", Qa2b(1), Qa2b(2), Qa2b(3), Qa2b(4));
Vb_ = Ca2b*Va;
fprintf("通过Ca2b 将Va转成Vb: %.3f %.3f %.3f, 约等于: %.3f %.3f %.3f \n", Vb_(1), Vb_(2), Vb_(3), Vb(1), Vb(2), Vb(3));
运行结果:
a2b的四元数为:0.960 0.275 0.047 0.004
通过Ca2b 将Va转成Vb: 0.455 -0.432 0.716, 约等于: 0.465 -0.447 0.712
4.2 利用四元数实现向量的不同坐标系转化
Qa2b = ch_qmul(ch_qconj(Qb2n), Qa2n);
Vb_ = ch_qmulv(Qa2b, Va);fprintf("通过Qa2b 将Va转成Vb: %.3f %.3f %.3f, 约等于: %.3f %.3f %.3f \n", Vb_(1), Vb_(2), Vb_(3), Vb(1), Vb(2), Vb(3));Qb2a = ch_qconj(Qa2b);Va_ = ch_qmulv(Qb2a, Vb);fprintf("通过Qb2a 将Vb转成Va: %.3f %.3f %.3f, 约等于: %.3f %.3f %.3f \n", Va_(1), Va_(2), Va_(3), Va(1), Va(2), Va(3));运行结果:
通过Qa2b 将Va转成Vb: 0.455 -0.432 0.716, 约等于: 0.465 -0.447 0.712
通过Qb2a 将Vb转成Va: 0.384 0.006 0.879, 约等于: 0.375 0.021 0.876
a系 转到 b系 = 先a系到n系,然后n系到b系
- n系到b系的旋转矩阵 = b系转到n系的旋转矩阵的转置
- n系到b系的四元数 = b系转到n系的四元数取负,后三位取负
然后就是旋转矩阵相乘,或是四元数相乘,这里需要注意顺序: b>n * a>n = a>n
这篇关于惯性导航学习过程记录(旋转矩阵部分)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





