CFD可压缩流（一）

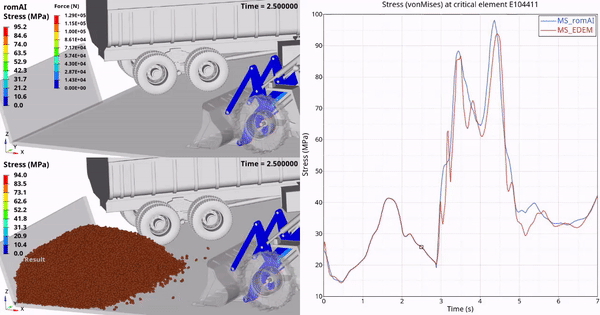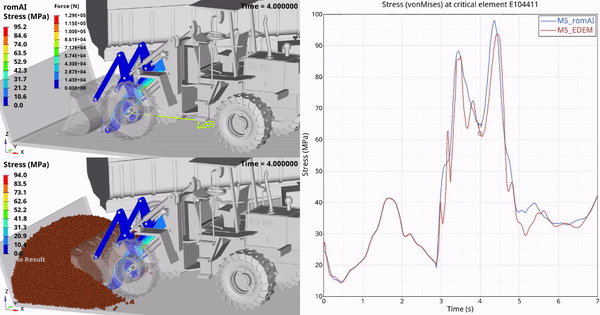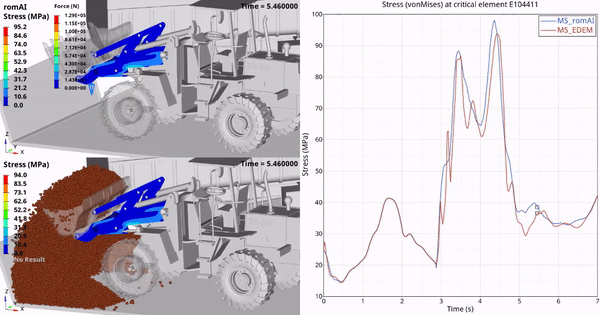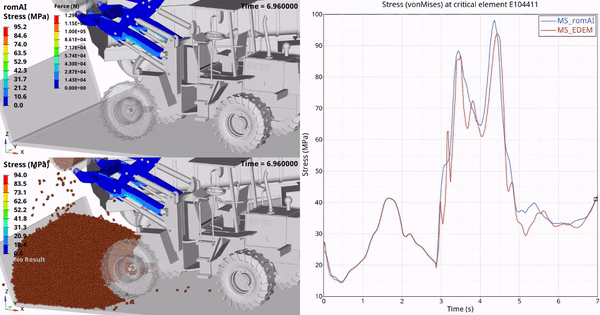
本文主要是介绍CFD可压缩流（一），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

课程名称	时间	地点	备注
微分拓扑选讲	周一（10-11）单周五5-6	二教314
计算流体力学	周三7-9	三教507
偏微分方程选讲	周二1-2 双周四1-2	理教412

考虑$u_t+au_x=0,x \in \mathbb{R},x_j=jh,j\in \mathbb{Z}$
设$\tau$表示时间步长，$h$表示空间步长，写出它的三种格式：

• 左偏心差分格式 $$u_j^{n+1}=u_j^n-\frac{a\tau}{h}(u^n_j-u^n_{j-1})\tag{2.5}$$ 稳定条件$0\leqslant ar<1$

  • 右偏心差分格式：

    un+1j=unj−aτh(unj+1−unj)(2.6)
    $$u_j^{n+1}=u_j^n-\frac{a\tau}{h}(u^n_{j+1}-u^n_{j})\tag{2.6}$$ 稳定条件$-1 \leqslant ar <0$

  • 中心差分格式：

    un+1j=unj−aτ2h(unj+1−unj−1)(2.7)
    $$u_j^{n+1}=u_j^n-\frac{a\tau}{2h}(u^n_{j+1}-u^n_{j-1})\tag{2.7}$$ 恒不稳定

  • CIR格式：将（2.4）（2.5）统一写成： $$u_j^{n+1}=u_j^n-\frac{a\tau}{2h}(u^n_{j+1}-u^n_{j-1})+\frac{|a\tau|}{2}(u^n_{j+1}-2u^n_j+u^n_{j-1})\tag{2.9}$$ ;CIR 格式就是在（2.7）的基础上添加了二阶差分项$\frac{|ar|}{2}\delta_x^2 u^n_j$作数值粘性项。
  • Lax-Friedrichs 格式： $$u_j^{n+1}=\frac{1}{2}(u^n_{j+1}+u^n_{j-1})-\frac{a\tau}{2h}(u^n_{j+1}-u^n_{j-1})\tag{2.12}$$ 等价的写成带粘性项的 $$u_j^{n+1}=u^n_{j}+\frac{1}{2}(u^n_{j+1}+u^n_{j-1}-2u^n_{j})-\frac{a\tau}{2h}(u^n_{j+1}-u^n_{j-1})\tag{2.14}$$ 其实就是将（2.7）的$u^n_j$写成了$\frac{1}{2}(u^n_{j+1}+u^n_{j-1})$,它的稳定性条件是 $$|a|r\leqslant 1\tag{2.13}$$ .观察（2.14）就相当于添加了数值粘性项$1/2\delta^2_{x}u^n_j$
  • Lemma在条件（2.13）下，CIR格式（2.9）和LF格式（2.12）的数值解$\{u^{n+1}_j\}$均满足$TV(u^{n+1}) \leqslant TV(u^n)$.其中$TV:=\sum_{j\in\mathbb{Z}}|u_{j+1}-u_j|$表示查分接的总变差。

这篇关于CFD可压缩流（一）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---