static void Main(string[] args){ForeachLeft();//韩信点兵 }public static void ForeachLeft(){int[] arr = new int[5] { 1, 3, 5, 8, 6 };int[] result = loopleft(3, arr);foreach (var item in result){Console.WriteLine(item);}Console.ReadKey();}public static int[] loopleft(int n, int[] arr){if (arr==null||arr.Length==0){return arr;}reverse(0, n - 1, ref arr);reverse(n , arr.Length - 1, ref arr);reverse(0, arr.Length - 1, ref arr);return arr;}public static void reverse(int left, int right, ref int[] arr){int temp = 0;while (left < right){temp = arr[left];arr[left] = arr[right];arr[right] = temp;left++;right--;}}
自从“韩信点兵,多多益善”事件之后,韩信的麻烦事就来了。这不,今天刘邦又找他麻烦了。
刘邦:爱将,近日朕看你早早就下班了,怎么回事呀?
韩信:陛下明鉴,臣点兵时有技巧,效率极高,陛下安排的工作任务臣均已完成。而本朝建立以来实行弹性工作制,于是臣就回家了。
刘邦:你小子是真不知道朕的苦衷啊!朕的大汉朝刚刚建立,百废待兴,你就不能为朕分忧,为大汉朝多做点贡献吗?
韩信:何事叨扰陛下?请陛下明示,臣必当竭尽全力!
(刘邦心理活动:我哪有什么事情让你去做呀?让你办事只是借口啦!只不过是担心你下班那么早,空闲下来谋划策反之事罢了。不得不防啊!为了不让你那么早下班,是得随便找个事拖拖你。)
突然,刘邦想了个法子。
刘邦:既然你点兵是个能手,朕就交你一事。从明天上班开始,你在点兵之前,要先将你的士兵循环左移,左移完毕,让我审查,再开始点兵。
说着,刘邦用木棍在地上画了起来。
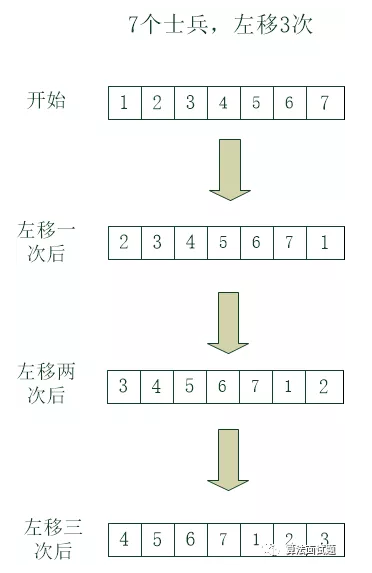
刘邦:假如现在有7个士兵,循环左移3次,移动结果如上图。
韩信:陛下,这好办,在移动时,我只要先让前三个士兵出列,然后让后面的兵依次向前移动三个位置,最后把前三个兵插入到队尾即可。
刘邦:那我如果让你左移4次、5次,你是不是要分别出列4个、5个人呢?不行,限制你每次只能出列1个人。
(注:从算法角度分析,这其实是限制了空间复杂度为O(1))
(韩信心理活动:如果每次只能出列一个人的话,我就得按刘老板画得那样,第一次先将1号士兵出列,然后让其他士兵依次向前移动一个位置,最后再把1号士兵插入队尾,对于2号、3号士兵也当如此。忽然,他想到了一个问题,在点兵前为什么要进行左移这个活动呢?没什么意义呀。)
正当他想问刘邦,此时刘邦瞪了他一眼,于是他赶紧改变主意,回复遵命。毕竟,快过年了,年终奖要紧。
就这样,接下来的日子里,韩信在点兵前都要进行这样一项活动,可是,随着时间一天天流逝,韩信发现刘老板给他的兵越来越多了,兵少时没关系,进行左移活动也用不了多少时间,而兵多了就麻烦了,常常使自己加班加到很晚才能下班。
(PS:刘老板对韩信已有怀疑之心,可为什么还要给他越来越多的兵呢?没错,他在试探韩信,当韩信拥兵众多时会不会谋反。)
求助
无法忍受这样无休止的加班,韩信来拜访张良。见到张良,将自己的情况一五一十给张良道明。
张良:初创公司都这样,加班是常事,习惯就好了。
韩信:可我觉得不是加班那么简单,刘老板似乎故意在找我麻烦。
张良:你可知刘老板为何要找你麻烦呀?
韩信:实在是无所得知啊!
张良:当真不知?
韩信:不知。
张良:你可知功高盖主的道理呀?
韩信:你是指老板担心我取代他。
张良:是呀,外边都在说你“韩信点兵,多多益善”,有句话“狡兔死,走狗烹,飞鸟尽,良弓藏”,你不得不记在心上呀!
(韩信直冒冷汗)
韩信:谨记教诲,而当务之急是先把这个士兵左移问题解决了,否则,我可能因此而被杀头。
张良拿起木棍在地上画了起来,不一会儿,有了答案。
张良:还拿你刚刚说的例子为例,如下图,有7个士兵,循环左移3位,你可以将此问题分为3步:
-
将队列分为两部分,左移3位就从第三个士兵后面划分;
-
分别对左右两部分逆序,具体逆序过程:将第一个士兵与最后一个士兵交换位置,将第二个士兵与倒数第二个交换位置,以此类推。具体交换时,比如1号士兵与3号士兵,可以先让1号士兵出列,3号填补到1号位置上,再把1号入列到3号位置上,这样也满足了刘老板规定的每次只能出列一个士兵。
-
再对整个队列进行一次逆序,完毕。

韩信感激涕零,觉得张良的方法效率太高了,谢过张良后,告辞了。
(注:韩信原来的方法时间复杂度为O(nL),张良的方法时间复杂度为O(L),其中n为移动位数,L为数组长度)





