本文主要是介绍DataWhale-树模型与集成学习-Task03-集成模式-202110,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
一、侧边栏练习题
1. 练习1


解答:
由于是白噪声,所以
最后一项推导如下:
根据上面的推导,很容易看出第四个等号成立。
2. 练习2

解答:
(1) 如果一个模型预测值都与真实值一致,那么可以偏差方差都很小。
(2)
偏差度量了学习算法的期望预测与真实结果的偏离程度,刻画了学习算法本身的拟合能力。
方差度量了同样大小的训练集的变动所导致的学习性能的变化,刻画了数据扰动所造成的影响。
噪声表达了当前任务上任何学习算法所能达到的期望泛化误差的下界,也就是最小值。
泛化误差可以分解为偏差、方差和噪声之和。
1) 训练程度不足时,学习器的拟合能力不够强,训练数据的扰动不足以使学习器产生显著变化,偏差将主导泛化错误率。
2)训练程度加深,学习器的拟合能力逐渐增强,训练数据发生的扰动逐渐能够被学习器学到,方差将主导泛化错误率。
3)训练程度充足后,学习器的拟合能力已经非常强,训练数据发生的轻微扰动都会导致学习器发生显著变化。训练数据非全局的特征如果被学习器学到了,将发生过拟合。
3. 练习3

解答:(解答链接),假设T为所有n个样本都至少被抽出一次的轮数,表示已经抽到了i-1个不重复样本后,抽到第i个不重复样本所用的轮数。则有
,对于
,抽到一个新样本的概率为:
因此的期望为:
由此可以得到:
100个样本全部抽出期望次数为100*H(100)。
4.练习4
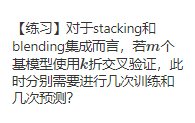
解答:对于stacking 需要训练m*k+1次,预测2m*k+1次。
对于blending需要训练m+1次,预测2m+1次。
二、知识回顾
1. 什么是偏差和方差分解?偏差是谁的偏差?此处的方差又是指什么?
解答:泛化误差可以分解为偏差、方差和噪声之和。偏差度量了学习算法的期望预测与真实结果的偏离程度,刻画了学习算法本身的拟合能力。方差度量了同样大小的训练集的变动所导致的学习性能的变化,刻画了数据扰动所造成的影响。
2. 相较于使用单个模型,bagging和boosting方法有何优势?
解答:bagging可以降低整体模型的方差,boosting可以降低整体模型的偏差。
3.请叙述stacking的集成流程,并指出blending方法和它的区别
解答:m个不同的基学习器。对于每个基模型,对数据集进行k折,k-1份做训练集,1份做验证集,依次取遍每1折做验证集其余做训练集,训练得到k个模型以及k份验证集上的相应预测结果,这些预测结果恰好能够拼接起来作为基模型在训练集上的学习特征,同时还要用这k个模型对测试集进行预测,并将结果进行平均作为该基模型的输出
。对每个基模型进行上述操作后,我们就能得到对应的训练集特征
, 以及测试集特征
。
此时,使用一个最终模型f, 以为特征,以训练集的样本标签为目标进行训练,在f完成训练后,以
为模型的输入,得到的输出结果作为整个集成模型的输出。
blending的区别就是不做k折,只按照一定比例划分出训练集和验证集。其缺陷在于不能使用全部的训练数据,稳健性较stacking差。
三、stacking代码实现
from sklearn.model_selection import KFold
from sklearn.neighbors import KNeighborsRegressor
from sklearn.tree import DecisionTreeRegressor
from sklearn.linear_model import LinearRegression
from sklearn.datasets import make_regressionimport numpy as np
import pandas as pdm1=KNeighborsRegressor()
m2=DecisionTreeRegressor()
m3=LinearRegression()models=[m1,m2,m3]#from sklearn.svm import LinearSVRfinal_model=DecisionTreeRegressor()k,m=4,len(models)if __name__=="__main__":X,y=make_regression(n_samples=1000,n_features=8,n_informative=4,random_state=0)final_X,final_y=make_regression(n_samples=500,n_features=8,n_informative=4,random_state=0)final_train=pd.DataFrame(np.zeros((X.shape[0],m)))final_test=pd.DataFrame(np.zeros((final_X.shape[0],m)))kf=KFold(n_splits=k)for model_id in range(m):model=models[model_id]for train_index,test_index in kf.split(X):X_train,X_test=X[train_index],X[test_index]y_train,y_test=y[train_index],y[test_index]model.fit(X_train,y_train)final_train.iloc[test_index,model_id]=model.predict(X_test)final_test.iloc[:,model_id]+=model.predict(final_X)final_test.iloc[:,model_id]/=kfinal_model.fit(final_train,y)res=final_model.predict(final_test)
四、blending代码实现
from sklearn.model_selection import KFold
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsRegressor
from sklearn.tree import DecisionTreeRegressor
from sklearn.linear_model import LinearRegression
from sklearn.datasets import make_regressionimport numpy as np
import pandas as pdm1=KNeighborsRegressor()
m2=DecisionTreeRegressor()
m3=LinearRegression()models=[m1,m2,m3]final_model=DecisionTreeRegressor()m=len(models)if __name__=="__main__":X,y=make_regression(n_samples=1000,n_features=8,n_informative=4,random_state=0)final_X,final_y=make_regression(n_samples=500,n_features=8,n_informative=4,random_state=0)X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.5)final_train=pd.DataFrame(np.zeros((X_test.shape[0],m)))final_test=pd.DataFrame(np.zeros((final_X.shape[0],m)))for model_id in range(m):model=models[model_id]model.fit(X_train,y_train)final_train.iloc[:,model_id]=model.predict(X_test)final_test.iloc[:,model_id]+=model.predict(final_X)final_model.fit(final_train,y_train)res=final_model.predict(final_test)这篇关于DataWhale-树模型与集成学习-Task03-集成模式-202110的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




