本文主要是介绍# [cs231n (八)神经网络总结:最小网络案例研究 ][1],希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
cs231n (八)神经网络总结:最小网络案例研究
标签(空格分隔): 神经网络
文章目录
- [cs231n (八)神经网络总结:最小网络案例研究 ][1]
- 同类文章
- 0.回顾
- 1. 引言
- 2. 生成一些数据
- 3. 训练一个softmax线性分类器
- 1. 初始化参数
- 2. 计算分数
- 3. 计算loss
- 4. 反向传播法计算梯度
- 6. 现在就可以合并一下得到softmax分类器
- 4. 训练神经网络
- 5. 总结
- 转载和疑问声明
- 我祝各位帅哥,和美女,你们永远十八岁,嗨嘿嘿~~~
同类文章
cs231n (一)图像分类识别讲了KNN
cs231n (二)讲了线性分类器:SVM和SoftMax
cs231n (三)优化问题及方法
cs231n (四)反向传播
cs231n (五)神经网络 part 1:构建架构
cs231n (六)神经网络 part 2:传入数据和损失
cs231n (七)神经网络 part 3 : 学习和评估
cs231n (八)神经网络总结:最小网络案例研究
cs231n (九)卷积神经网络
0.回顾
cs231n (一)图像分类识别讲了KNN
cs231n (二)讲了线性分类器:SVM和SoftMax
cs231n (三)优化问题及方法
cs231n (四)反向传播
cs231n (五)神经网络 part 1:构建架构
cs231n (六)神经网络 part 2:传入数据和损失
cs231n (七)神经网络 part 3 : 学习和评估
1. 引言
经过前面近七节课的学习训练,我们有了深厚理论基础,和毛毛草草的向量化编程基础、调优基础。。。这牛逼吹的怕了都。
那么现在我们应该开始自己动手解决一个实际问题吧:快来啊。
首先实现线性分类器,然后拓展到神经网络,只要线性网络构建好了,我们拓展到神经网络就会很简单很简单很jian。
2. 生成一些数据
先生成一个螺旋离散数据
N = 100 # number of points per class
D = 2 # dimensionality
K = 3 # number of classes
X = np.zeros((N*K,D)) # data matrix (each row = single example)
y = np.zeros(N*K, dtype='uint8') # class labels
for j in range(K):ix = range(N*j,N*(j+1))r = np.linspace(0.0,1,N) # radiust = np.linspace(j*4,(j+1)*4,N) + np.random.randn(N)*0.2 # thetaX[ix] = np.c_[r*np.sin(t), r*np.cos(t)]y[ix] = j
# lets visualize the data:
plt.scatter(X[:, 0], X[:, 1], c=y, s=40, cmap=plt.cm.Spectral)
plt.show()
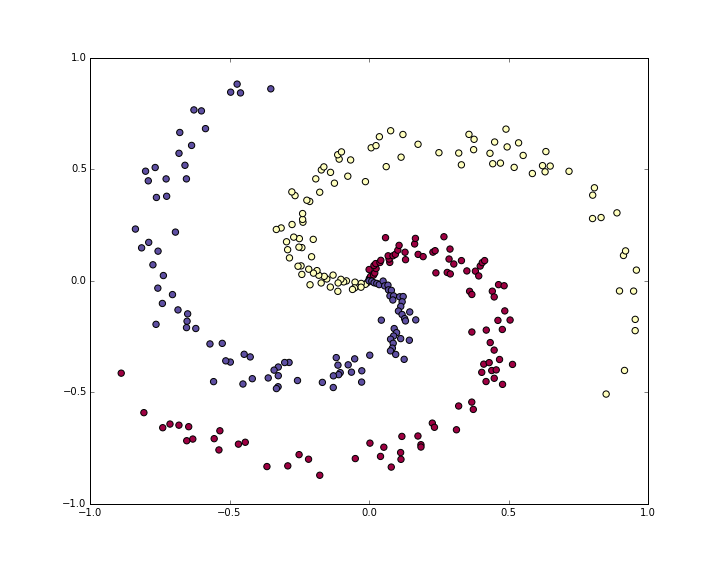
此时数据是非线性的, 对数据进行标准差标准化已经做过了。
3. 训练一个softmax线性分类器
1. 初始化参数
先在这个分类数据集上训练一个Softmax分类器,Softmax分类器具有线性分数函数,并使用交叉熵损失。
线性分类器的参数由每个类别的权重矩阵W和偏差矢量b组成,先将这些参数初始化为随机数:
# initialize parameters randomly
W = 0.01 * np.random.randn(D,K)
b = np.zeros((1,K))
W = DxC = 2x3
2. 计算分数
得到分数很简答啊:
# compute class scores for a linear classifier
scores = np.dot(X, W) + b
X = NxD = 300x2
scores = NxC
3. 计算loss
损失函数是得到区分目标的关键:其实就是正确的类得分是最高的,并且损失是最低的,如果分类正确。
这里使用的是softmax相关的交叉熵损失,损失函数应该是:
L i = − l o g ( e f y i ∑ j e f j ) \displaystyle Li=-log(\frac{e^{f_{y_i}}}{\sum_je^{f_j}}) Li=−log(∑jefjefyi)
softmax 函数把每一个数据得到三个分数,按照上述公式得到的是标准化概率,并且:
当正确类别概率很小,那么loss会趋近于无穷的。
当正确类别概率接近于1,那么loss会趋近于0的, 因为log(1)=0
$$L = \underbrace{ \frac{1}{N} \sum_i L_i }\text{data loss} + \underbrace{ \frac{1}{2} \lambda \sum_k\sum_l W{k,l}^2 }_\text{regularization loss} \\$$
我们计算得到了分数,那么损失可由上述狮子计算
num_examples = X.shape[0]
# get unnormalized probabilities
exp_scores = np.exp(scores)
# normalize them for each example
probs = exp_scores / np.sum(exp_scores, axis=1, keepdims=True)
现在得到的概率是:[300 x 3], 每行有三个数值,理论上最大的那个就是对应的正确分类的分数。
corect_logprobs = -np.log(probs[range(num_examples),y])
这里只分配概率给正确分类,损失就是这些对数概率和正则化损失的均值
# compute the loss: average cross-entropy loss and regularization
data_loss = np.sum(corect_logprobs)/num_examples
reg_loss = 0.5*reg*np.sum(W*W)
loss = data_loss + reg_loss
损失越低意味着正确分类的概率越高。
4. 反向传播法计算梯度
这里引入 p k = e f k ∑ j e f j L i = − log ( p y i ) p_k = \frac{e^{f_k}}{ \sum_j e^{f_j} } \hspace{1in} L_i =-\log\left(p_{y_i}\right) pk=∑jefjefkLi=−log(pyi),
可以使用链式法则:
∂ L i ∂ f k = p k − 1 ( y i = k ) \frac{\partial L_i }{ \partial f_k } = p_k - \mathbb{1}(y_i = k) ∂fk∂Li=pk−1(yi=k)
好简单哈 p = [0.2, 0.3, 0.5], 0.3是正确的分类, 那么 df = [0.2, -0.7, 0.5]
增加分数向量f的第一个或最后一个元素(不正确类别的分数)会增加损失(由于+0.2和+0.5的正号)增加损失是不好的分类。
然而,增加正确分数的分数对损失有负面影响。 -0.7的梯度告诉我们,增加正确的分数会导致损失 Li 的减少,这是合理的。
probs存储每个例子的所有类(作为行)的概率,为了获得分数上的梯度dscores。
dscores = probs
dscores[range(num_examples),y] -= 1
dscores /= num_examples
最后,我们得到的分数 s c o r e s = n p . d o t ( X , W ) + b scores = np.dot(X,W)+ b scores=np.dot(X,W)+b ,所以分数梯度保存在dscores中),我们现在可以反向传播到W和b:
dW = np.dot(X.T, dscores)
db = np.sum(dscores, axis=0, keepdims=True)
dW += reg*W # don't forget the regularization gradient
###5. 如何参数更新?
现在指导了梯度,指导参数如何影响损失函数,那么就开始更新梯度啦,就是稍微减少点梯度,其实就是迭代啦。
# perform a parameter update
W += -step_size * dW
b += -step_size * db
6. 现在就可以合并一下得到softmax分类器
#Train a Linear Classifier# initialize parameters randomly
W = 0.01 * np.random.randn(D,K)
b = np.zeros((1,K))# some hyperparameters
step_size = 1e-0
reg = 1e-3 # regularization strength# gradient descent loop
num_examples = X.shape[0]
for i in xrange(200):# evaluate class scores, [N x K]scores = np.dot(X, W) + b # compute the class probabilitiesexp_scores = np.exp(scores)probs = exp_scores / np.sum(exp_scores, axis=1, keepdims=True) # [N x K]# compute the loss: average cross-entropy loss and regularizationcorect_logprobs = -np.log(probs[range(num_examples),y])data_loss = np.sum(corect_logprobs)/num_examplesreg_loss = 0.5*reg*np.sum(W*W)loss = data_loss + reg_lossif i % 10 == 0:print "iteration %d: loss %f" % (i, loss)# compute the gradient on scoresdscores = probsdscores[range(num_examples),y] -= 1dscores /= num_examples# backpropate the gradient to the parameters (W,b)dW = np.dot(X.T, dscores)db = np.sum(dscores, axis=0, keepdims=True)dW += reg*W # regularization gradient# perform a parameter updateW += -step_size * dWb += -step_size * db
结果大概是这个样子的。
iteration 0: loss 1.096956
iteration 10: loss 0.917265
iteration 20: loss 0.851503
iteration 30: loss 0.822336
iteration 40: loss 0.807586
iteration 50: loss 0.799448
iteration 60: loss 0.794681
iteration 70: loss 0.791764
iteration 80: loss 0.789920
iteration 90: loss 0.788726
iteration 100: loss 0.787938
iteration 110: loss 0.787409
iteration 120: loss 0.787049
iteration 130: loss 0.786803
iteration 140: loss 0.786633
iteration 150: loss 0.786514
iteration 160: loss 0.786431
iteration 170: loss 0.786373
iteration 180: loss 0.786331
iteration 190: loss 0.786302
经过190次迭代,可以得到训练精度:
# evaluate training set accuracy
scores = np.dot(X, W) + b
predicted_class = np.argmax(scores, axis=1)
print 'training accuracy: %.2f' % (np.mean(predicted_class == y))
准确率是 49%, 看一下学习到边界
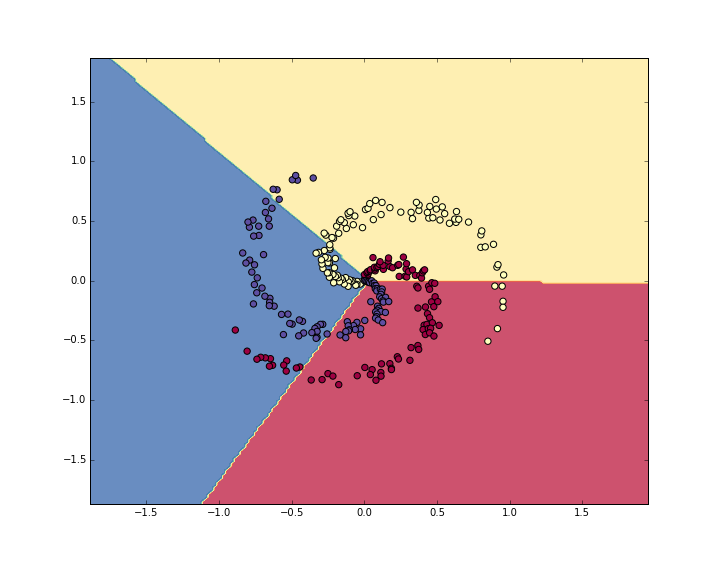
4. 训练神经网络
其实对于非线性边界用线性分类器确实有点难,现在我们构建一个简单的二层神经网络。
第一层第二层就是这么简单:
# initialize parameters randomly
h = 100 # size of hidden layer
W = 0.01 * np.random.randn(D,h)
b = np.zeros((1,h))
W2 = 0.01 * np.random.randn(h,K)
b2 = np.zeros((1,K))
前向传播的分数可以这样得到:
# evaluate class scores with a 2-layer Neural Network
hidden_layer = np.maximum(0, np.dot(X, W) + b) # note, ReLU activation
scores = np.dot(hidden_layer, W2) + b2
在隐含层添加非线性单元------ReLU。
然后计算loss,分数梯度dscores都和之前一样。
计算梯度的时候先BP到第二层网络,这里也和之前的softmax类似。
# backpropate the gradient to the parameters
# first backprop into parameters W2 and b2
dW2 = np.dot(hidden_layer.T, dscores)
db2 = np.sum(dscores, axis=0, keepdims=True)
由于中间加了一个隐含层,所以我们需要计算隐含层的梯度:
dhidden = np.dot(dscores, W2.T)
还需要回传ReLUd的非线性,很简答啊
r = m a x ( 0 , x ) , d r d x = 1 ( x > 0 ) r = max(0, x), \frac{dr}{dx} = 1(x > 0) r=max(0,x),dxdr=1(x>0)
可以知道梯度通过如果x > 0, 梯度为零如果x < 0
# backprop the ReLU non-linearity
dhidden[hidden_layer <= 0] = 0
那么计算第一层的权重和梯度就是:
# finally into W,b
dW = np.dot(X.T, dhidden)
db = np.sum(dhidden, axis=0, keepdims=True)
好了我们已经完成整个过程了,总结一下。
# initialize parameters randomly
h = 100 # size of hidden layer
W = 0.01 * np.random.randn(D,h)
b = np.zeros((1,h))
W2 = 0.01 * np.random.randn(h,K)
b2 = np.zeros((1,K))# some hyperparameters
step_size = 1e-0
reg = 1e-3 # regularization strength# gradient descent loop
num_examples = X.shape[0]
for i in xrange(10000):# evaluate class scores, [N x K]hidden_layer = np.maximum(0, np.dot(X, W) + b) # note, ReLU activationscores = np.dot(hidden_layer, W2) + b2# compute the class probabilitiesexp_scores = np.exp(scores)probs = exp_scores / np.sum(exp_scores, axis=1, keepdims=True) # [N x K]# compute the loss: average cross-entropy loss and regularizationcorect_logprobs = -np.log(probs[range(num_examples),y])data_loss = np.sum(corect_logprobs)/num_examplesreg_loss = 0.5*reg*np.sum(W*W) + 0.5*reg*np.sum(W2*W2)loss = data_loss + reg_lossif i % 1000 == 0:print "iteration %d: loss %f" % (i, loss)# compute the gradient on scoresdscores = probsdscores[range(num_examples),y] -= 1dscores /= num_examples# backpropate the gradient to the parameters# first backprop into parameters W2 and b2dW2 = np.dot(hidden_layer.T, dscores)db2 = np.sum(dscores, axis=0, keepdims=True)# next backprop into hidden layerdhidden = np.dot(dscores, W2.T)# backprop the ReLU non-linearitydhidden[hidden_layer <= 0] = 0# finally into W,bdW = np.dot(X.T, dhidden)db = np.sum(dhidden, axis=0, keepdims=True)# add regularization gradient contributiondW2 += reg * W2dW += reg * W# perform a parameter updateW += -step_size * dWb += -step_size * dbW2 += -step_size * dW2b2 += -step_size * db2## This prints:iteration 0: loss 1.098744
iteration 1000: loss 0.294946
iteration 2000: loss 0.259301
iteration 3000: loss 0.248310
iteration 4000: loss 0.246170
iteration 5000: loss 0.245649
iteration 6000: loss 0.245491
iteration 7000: loss 0.245400
iteration 8000: loss 0.245335
iteration 9000: loss 0.245292
训练精度是:98%! 厉害了,老铁
# evaluate training set accuracy
hidden_layer = np.maximum(0, np.dot(X, W) + b)
scores = np.dot(hidden_layer, W2) + b2
predicted_class = np.argmax(scores, axis=1)
print 'training accuracy: %.2f' % (np.mean(predicted_class == y))
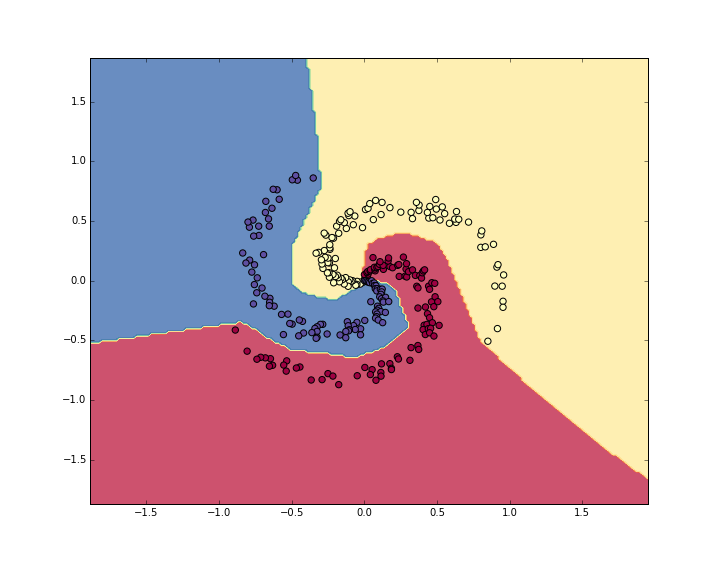
5. 总结
其实从线性到网络我们变化的代码很少,Loss只变了一行,反向传播只不过是加了“中间变量”。
转载和疑问声明
如果你有什么疑问或者想要转载,没有允许是不能转载的哈
赞赏一下能不能转?哈哈,联系我啊,我告诉你呢 ~~
欢迎联系我哈,我会给大家慢慢解答啦~~~怎么联系我? 笨啊~ ~~ 你留言也行
你关注微信公众号1.机器学习算法工程师:2.或者扫那个二维码,后台发送 “我要找朕”,联系我也行啦!

(爱心.gif) 么么哒 ~么么哒 ~么么哒
码字不易啊啊啊,如果你觉得本文有帮助,三毛也是爱!
我祝各位帅哥,和美女,你们永远十八岁,嗨嘿嘿~~~


这篇关于# [cs231n (八)神经网络总结:最小网络案例研究 ][1]的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





