# cs231n （四）反向传播

本文主要是介绍# cs231n （四）反向传播，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

cs231n （四）反向传播

标签（空格分隔）：神经网络

文章目录

cs231n （四）反向传播
0.回顾
1.引言
2. 通过简单表达式理解梯度
3. 链式法则计算复合函数
4. 如何理解反向传播
5. 模块化：Sigmoid
6. 实践反向传播：分段
7. 反向梯度流的模式
8. 向量化计算梯度啦
9. 总结一下呗
10 下节预告
转载和疑问声明
我祝各位帅哥，和美女，你们永远十八岁，嗨嘿嘿~~~

0.回顾

cs231n （一）图像分类识别讲了KNN
cs231n （二）讲了线性分类器：SVM和SoftMax
cs231n （三）优化问题及方法

回顾上次的内容，其实就会发现，虽然我们构造好了损失函数，可以简单使用导数的定义解决损失函数优化问题，但是并不高效啊，现在探索一下呗。

1.引言

其实这次呢，就是让你学会：

反向传播形成直观而专业的理解
利用链式法则递归计算表达式的梯度
理解反向传播过程及其牛逼之处

如果你想：理解、实现、设计和调试神经网络，请再看一遍哈哈！

目的： 给出 $f (x)$ （x是输入数据的向量），计算 $\nabla f(x)$ .
学生：如果我会了链式法则，或者偏微分是不是不用看了？
老师：你试试看啊，期末能不能过了。

2. 通过简单表达式理解梯度

先看看二元乘法函数： $f (x, y) = x y$ ,求一下偏头痛，不，偏导数

$\displaystyle f(x,y)=xy \to \frac {df}{dx}=y \quad \frac {df}{dy}=x$

啥意思嘞？

请记住导数的意义：函数变量在某个点周围的很小区域内变化，而导数就是—>变量变化导致的函数在该方向上的变化率

$\frac{df(x)}{dx}= \lim \limits_{h\to 0} \frac{f(x+h)-f(x)}{h}$

$\nabla f(x) = \lim \limits_{h\to 0} \frac{f(x+h)-f(x)}{h}$

对比一下，哎，高数没学好。
官方解释：若 $x = 4, y = - 3$ ，则 $f (x, y) = - 12$ ，x的导数 $\frac{\partial f}{\partial x}=-3$ ，意思就是x 变大多少，表达式值就会变小三倍，变形看看！！！
$\frac{df(x)}{dx}$

导数说明了你有多敏感，就是你是不是chu…级学者，（邪恶.gif）

常用的还有取最大值法：

$\displaystyle f(x,y)=max(x,y) \to \frac {df}{dx}=1 (x>=y) \quad\frac {df}{dy}=1 (y>=x)$

if 目前x是大于另一个变量y的，那么梯度是1，反之为0咯。

3. 链式法则计算复合函数

这个都要说？

发现cs23n 真的把大家当傻子养啊，中国大学把大家当爱因斯坦虐啊

比如复合函数:

$f (x, y, z) = (x + y) z$

$\displaystyle\frac{\partial f}{\partial x}=\frac{\partial f}{\partial q}\frac{\partial q}{\partial x}$

两个梯度数值相乘就好了，简单吧，链式法则嘛，示例代码如下：

x = -2; y = 5; z = -4# Forward propogation
q = x + y # q becomes 3
f = q * z # f becomes -12# BP
# 函数整体法： f = q * z
dfdz = q # df/dz = q, z的梯度是3
dfdq = z # df/dq = z, q的梯度是-4
# return到q = x + y
dfdx = 1.0 * dfdq # dq/dx = 1. 链式法则核心就是乘，整体思想
dfdy = 1.0 * dfdq # dq/dy = 1

看看计算流是怎么样子的：

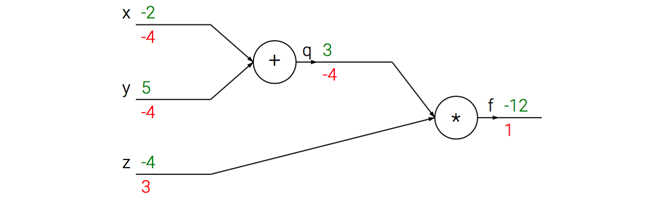
前向传播是输入到输出绿色，反向传播链式法则计算梯度是红色。

4. 如何理解反向传播

其实就是一个局部过程，每经过一个“神经元”-“节点”，可以得到两个东东：

此节点的输出值
局部梯度

咱么通过q = x+y 加法部分（类似电路中的门）：输入【-2，5】，输出【3】，其实你可以把整个过程想象成一个水流。

5. 模块化：Sigmoid

几乎任何微分的函数都可以看做门，不是门组合就是门拆分，看一个表达式：

$\displaystyle f(w,x)=\frac{1}{1+e^{-(w_0x_0+w_1x_1+w_2)}}$

如果只看做一个简单的输入为x和w，输出为一个值。

这个函数包含许多门，有加法、乘法、取最大值门，以及这4种：

$\displaystyle f(x)=\frac{1}{x} \to \frac{df}{dx}=-1/x^2$
$\displaystyle f_c(x)=c+x \to \frac{df}{dx}=1\displaystyle f(x)=e^x \to \frac{df}{dx}=e^x$
$\displaystyle f_a(x)=ax \to \frac{df}{dx}=a$

其中， $f_c$ 使用对输入值进行了常量c的平移， $f_a$ 将输入值扩大了a倍
我们看做一元门，因为要计算c,a的梯度。整个计算流如下：

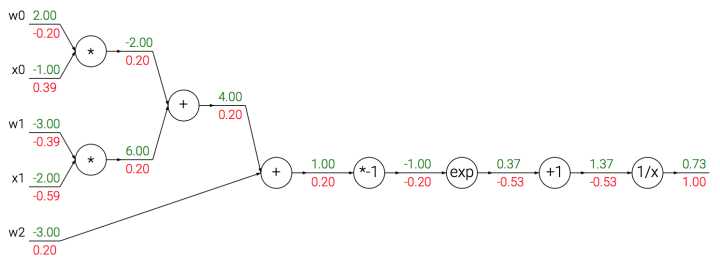
我们使用sigmoid函数的二维神经元例子：输入【x0, x1】得到权重【w0,w1,w2】

sigmoid函数也叫： $\sigma (x)$ ,其导数就是这样求的：

$\displaystyle\sigma(x)=\frac{1}{1+e^{-x}}$
$\displaystyle\to\frac{d\sigma(x)}{dx}=\frac{e^{-x}}{(1+e^{-x})^2}=(\frac{1+e^{-x}-1}{1+e^{-x}})(\frac{1}{1+e^{-x}})=(1-\sigma(x))\sigma(x)$

例子，sigmoid输入为1.0，则有输出0.73，那么局部梯度为(1-0.73)*0.73~=0.2
实际情况下就是封装到：一个单独的门单元中，实现代码：

w = [2,-3,-3] # 随机的初始值
x = [-1, -2]# 前向传播
dot = w[0]*x[0] + w[1]*x[1] + w[2]
f = 1.0 / (1 + math.exp(-dot)) # sigmoid# 对神经元BP
ddot = (1 - f) * f # sigmoid函数求导
dx = [w[0] * ddot, w[1] * ddot] # 回传到x
dw = [x[0] * ddot, x[1] * ddot, 1.0 * ddot] # 回传到w
# done

Hint：分段反向传播为了使反向传播更简单，因此把前向传播分成几个阶段。

6. 实践反向传播：分段

看！举个例子。

$\displaystyle f(x,y)=\frac{x+\sigma(y)}{\sigma(x)+(x+y)^2}$

我们不需要明确的函算梯度，如何使用反向传播计算梯度搞定就行。

x = 3 # 随机初始
y = -4
# 前向传播
sigy = 1.0 / (1 + math.exp(-y)) # 分子中的sigmoid        #(1)
num = x + sigy # 分子                                    #(2)
sigx = 1.0 / (1 + math.exp(-x)) # 分母中的sigmoid        #(3)
xpy = x + y                                              #(4)
xpysqr = xpy**2                                          #(5)
den = sigx + xpysqr # 分母                               #(6)
invden = 1.0 / den                                       #(7)
f = num * invden # done                                  #(8)

这样计算反向传播就简单了吧：前向传播时产生的变量(sigy, num, sigx, xpy, xpysqr, den, invden)进行反向传播，在反向传播的每一部分都包含表达式的local梯度.


# backprop f = num * invden
dnum = invden # gradient on numerator                             #(8)
dinvden = num                                                     #(8)
# backprop invden = 1.0 / den 
dden = (-1.0 / (den**2)) * dinvden                                #(7)
# backprop den = sigx + xpysqr
dsigx = (1) * dden                                                #(6)
dxpysqr = (1) * dden                                              #(6)
# backprop xpysqr = xpy**2
dxpy = (2 * xpy) * dxpysqr                                        #(5)
# backprop xpy = x + y
dx = (1) * dxpy                                                   #(4)
dy = (1) * dxpy                                                   #(4)
# backprop sigx = 1.0 / (1 + math.exp(-x))
dx += ((1 - sigx) * sigx) * dsigx # Notice += !! See notes below  #(3)
# backprop num = x + sigy
dx += (1) * dnum                                                  #(2)
dsigy = (1) * dnum                                                #(2)
# backprop sigy = 1.0 / (1 + math.exp(-y))
dy += ((1 - sigy) * sigy) * dsigy                                 #(1)
# done! phew

关于上述反向传播代码我说的一点就是链式法则：

$\displaystyle\frac{\partial f}{\partial x}=\frac{\partial f}{\partial num }\frac{\partial num}{\partial sigy}\frac{\partial sigy}{\partial x} ...$

说人话就是：

一个中间变量缓存
不同分支梯度要相加

7. 反向梯度流的模式

你把这个梯度流想象成水流
然后反向传播中的梯度可以直观化解释：加法就相当于两个相同的管子分流，乘法和取最大操作嘛，你也可以类比，什么例子呢？请私信告诉我吧、哈哈。

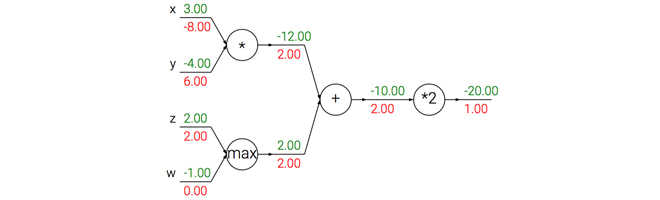
加法门：把输出的梯度相等地分发给它所有的输入
取最大：将梯度分配给最大的管子。
乘法门：得到输入激活数据，对它们进行交换，然后乘以梯度，上图中x的梯度是-4.00x2.00=-8.00 （好难理解喔~）

8. 向量化计算梯度啦

看看矩阵法（偷懒法）：


# FP
W = np.random.randn(5, 10)
X = np.random.randn(10, 3)
D = W.dot(X)# 假设D的梯度已知
dD = np.random.randn(*D.shape) # 初始化梯度
dW = dD.dot(X.T) 
dX = W.T.dot(dD)