算法43-欧拉信封问题

题目：

上面是著名的欧拉信封原题，我们将题目变化一下，假设有一个村庄，规定每个村民都要往外寄出一封信，但不能寄给自己，都要收到别人的一封信，假设有N位村民，有多少种寄法

分析：
从小样本开始枚举，看能不能递推出公式

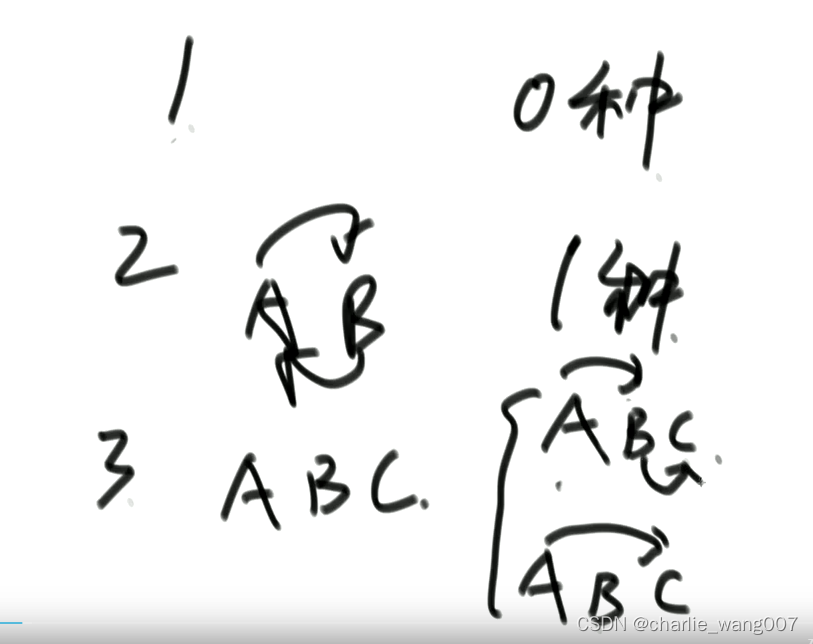
1个人----0种
2个人----互相寄，1种
3个人----2种

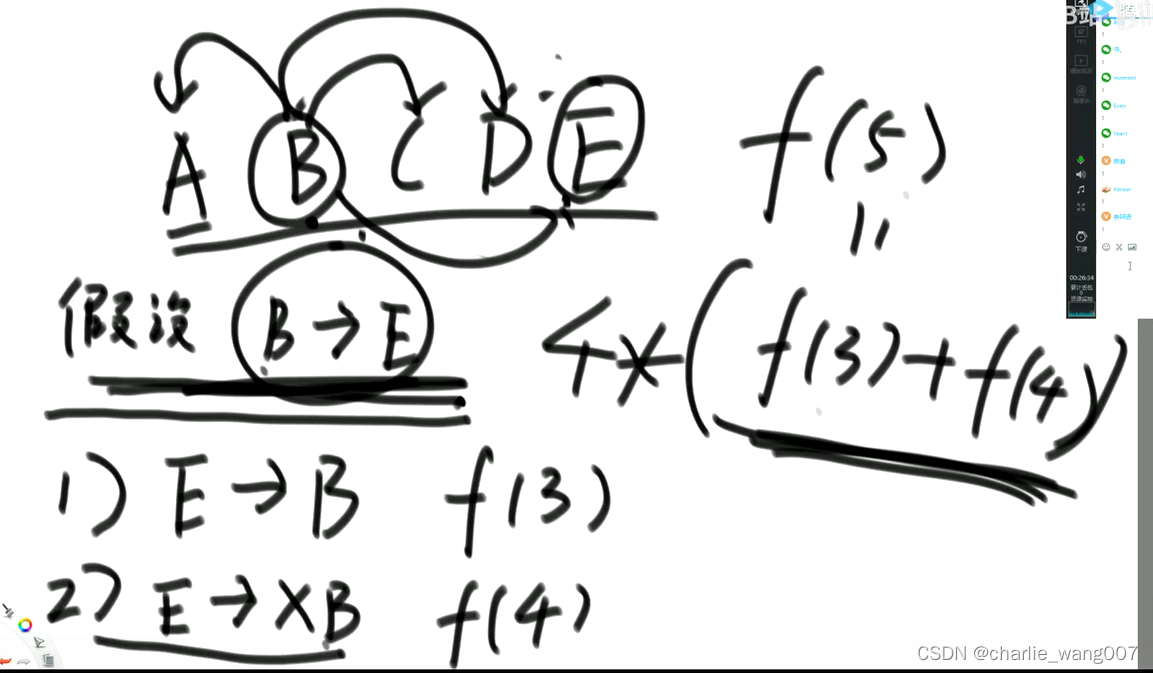
当n大于4，情况有如何呢

现在假设有五个人

1 假设B寄给E 有两种情况

1）E也寄给B，那么B和E完成寄和收，不会跟系统发生关系了，系统剩下三人
2）E寄出了但没有寄给B，B和E的动作完整一半，剩下一半，可以将他两个人合并为一个人，那么相当于剩下4个人

2 同B寄给E一样，B也可以寄给ACD，那么B寄出的情况就有4种

由此可以推导出当有5个人的时候

$f(5)=4\ast (f(3)+f(4))$

一般公式就是：

$f(n)=(n-1)\ast (f(n-1)+f(f-2))$

代码：

package main
import ("fmt"
)func mail(n int)int{if n==1{return 0}if n==2{return 1}if n==3{return 2}return (n-1)*(mail(n-1)+mail(n-2))
}func main(){fmt.Println(mail(6))
}