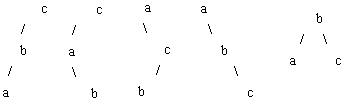本文主要是介绍NOIP 提高组 初赛 三、问题求解 习题集(二)NOIP2000-NOIP2005,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
NOIP 提高组 初赛 三、问题求解 习题集(二)NOIP2000-NOIP2005
1.第六届(NOIP2000)
问题:
1.已知,按中序遍历二叉树的结果为:abc
问:有多少种不同形态的二叉树可以得到这一遍历结果,并画出这些二叉树。
1.答:有 种不同形态的二叉树可以得到这一遍历结果; (1分)
可画出的这些二叉树为: (5分)
2.设有一个共有n级的楼梯,某人每步可走1级,也可走2级,也可走3级,用递推公式给出某人从底层开始走完全部楼梯的走法。例如:当n=3时,共有4种走法,即1+1+1,1+2,2+1,3。
2.用递推公式给出某人从底层开始走完全部楼梯的走法为(用F(N)记录不同方案数)
(6分)
问题解答:
1.先画出包含三个节点不同形态的二叉树5个,再根据中序遍历,在节点中填入相关数据。
(来自《算法竞赛入门经典》P155)
用递归定义 二叉树T 的先序遍历、中序遍历、后序遍历:
先序遍历 PreOrder(T)=T的根节点+PreOrder(T的左子树)+PreOrder(T的右子树)
中序遍历 InOrder(T)=InOrder(T的左子树)+T的根节点+InOrder(T的右子树)
后序遍历 PostOrder(T)=PostOrder(T的左子树)+PostOrder(T的右子树)+T的根节点2.看了答卷才知道,上面有提示(用F(N)记录不同方案数)。
F(1)=1
F(2)=2
F(3)=4
n=4有三种走法:
走1级,剩下的有F(4-1)走法;
走2级,剩下的有F(4-2)走法;
走3级,剩下的有F(4-3)走法;
F(4)=F(4-1)+F(4-2)+F(4-3)走法
归纳可得:F(N)=F(N-1)+F(N-2)+F(N-3)。
1.二叉树2.排列组合、递推
2.第七届(NOIP2001)
问题:
1.已知一棵二叉树的结点名为大写英文字母,其中序与后序遍历的顺序分别为:CBGEAFHDIJ与CGEBHFJIDA则该二叉树的先序遍历的顺序为:
2.平面上有三条平行直线,每条直线上分别有7,5,6个点,且不同直线上三个点都不在同一条直线上。问用这些点为顶点,能组成多少个不同四边形?
问题解答:
1.
(来自《算法竞赛入门经典》P155)
用递归定义 二叉树T 的先序遍历、中序遍历、后序遍历:
先序遍历 PreOrder(T)=T的根节点+PreOrder(T的左子树)+PreOrder(T的右子树)
中序遍历 InOrder(T)=InOrder(T的左子树)+T的根节点+InOrder(T的右子树)
后序遍历 PostOrder(T)=PostOrder(T的左子树)+PostOrder(T的右子树)+T的根节点 左 右 根
后:CGEB | HFJID | A
左 根 右
中:CBGE | A | FHDIJ
左 右 根
后:C | GE | B
左 根 右
中:C | B | EG
左 根
后:G | E
左 根
中:G | E
左 右 根
后:HF | JI | D
左 根 右
中:FH | D | IJ
右 根
后:H | F
根 右
中:F | H
左 根
后:J | I
左 根
中:I | J
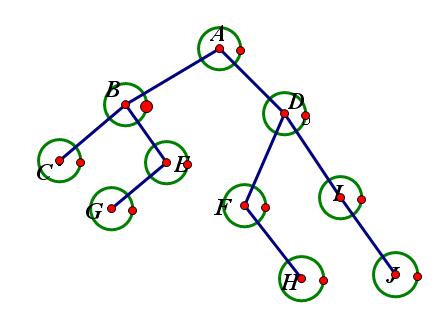
根据上述画出二叉树:
根据上述二叉树形态,前序遍历结果:ABCEGDFHIJ
2.
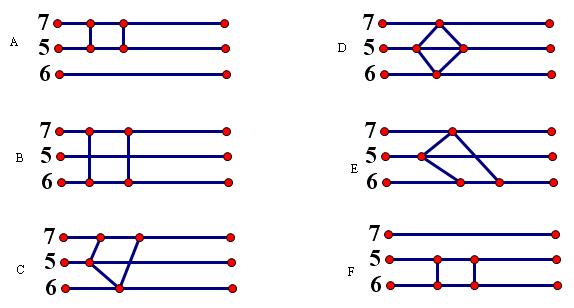
如上图所示,共有6种情况:
A(7选2,5选2) C(7,2)*C(5,2)=210
B(7选2,6选2) C(7,2)*C(6,2)=315
C(7选2,5选1,6选1) C(7,2)*C(5,1)*C(6,1)=630
E(7选1,5选1,6选2) C(7,1)*C(5,1)*C(6,2)=525
F(5选2,6选2) C(5,2)*C(6,2)=150
总数为210+315+630+420+525+150=2250
1.二叉树2.排列组合
3.第八届(NOIP2002)
问题:
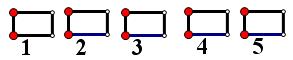
1. 在书架上放有编号为1 ,2,...,n的n本书。现将n本书全部取下然后再放回去,当放回去时要求每本书都不能放在原来的位置上。例如:n = 3时:
原来位置为:1 2 3
放回去时只能为:3 1 2 或 2 3 1 这两种
问题:求当n= 5时满足以上条件的放法共有多少种?(不用列出每种放法)
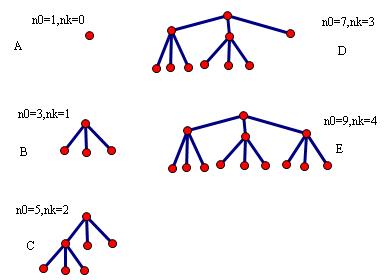
2. 设有一棵k叉树,其中只有度为0和k两种结点,设n 0 ,nk ,分别表示度为0和度为k的结点个数,试求出n0 和nk之间的关系(n0 = 数学表达式,数学表达式仅含nk 、k和数字)。
问题解答:
1.
考虑到P(5,5)=120,数量不大,决定
采用枚举的方式:盒1只能装(2,3,4,5),以以盒1装2为例,盒2只能装(1,3,4,5),以盒2装1为例,盒3只能装(4,5),
以盒3装4为例,盒4只能装(3,5),至此盒4装5,盒5装3,上述做法安放的是2 1 4 5 3。其他做法以次类推,统计如下:
盒1装2 共11种
盒1装3 共11种
盒1装4 共11种
盒1装5 共11种
总计44种。
上述方法成功率不高,费时费力,但这也是出题人所想。
寻求通法:
错排问题,通过三个页面找到。http://www.docin.com/p-723529192.html;http://max.book118.com/html/2016/0323/38491091.shtm;http://blog.csdn.net/liwen_7/article/details/7646451;最后找到了一个看懂的页面http://blog.sina.com.cn/s/blog_73e2747b0100ot5k.html;摘抄如下:
从中任取一个元素,不妨取1号元素,还剩n-1个元素,再从这n-1个元素对应的位置中选一个,共n-1种方法
第一种,1号元素放入2号位置且2号元素也放入1号位置,此时剩下n-2个元素继续错排,共F(n-2)种方法
第二种,1号元素放入2号位置但2号元素不放入1号位置,既然2号元素不放入1号位置,不妨把2号元素看作1号元
素,于是等价于新的1号元素不放入1号位置,那么剩下n-1个元素继续错排,共F(n-1)种方法
于是得到递推式F(n)=(n-1)*(F(n-2)+F(n-1))
点评:错排问题递推共识的学习,还是能上手的,但是,一张白纸,直接推到出递推公式,那是不可能的,与欧拉差距巨大啊。
2.查了二叉树度的概念https://zhidao.baidu.com/question/36114430.html:
子树就是二叉树的分支。度就是分支的数目。 没有分叉的二叉树节点的度就是0度。如果一个节点只有一个分叉就是1度。两个分叉就是2度的子树。
弄清了树 度 的概念。
假设k=3,画图找规律:
从上图可归纳:
有nk*k个度为0的节点,但其中有nk-1(这里的1是指根节点)个节点占用度为0节点的份额,故实际度为0的数目n0=nk*k-(nk-1)。
1.排列组合、递推2.二叉树
4.第九届(NOIP2003)
问题:
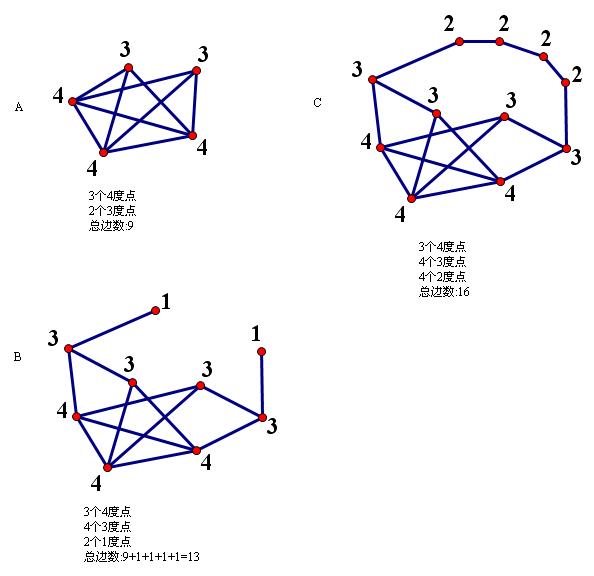
1. 无向图G有16条边,有3个4度顶点、4个3度顶点,其余顶点的度均小于3,则G至少_______个顶点。
2. 某年级学生共选修6门课程,期末考试前,必须提前将这6门课程考完,每人每天只在下午至多考一门课程,设6门课程为C1,C2,C3,C4,C5,C6,S(Ci)为学习Ci 的学生集合。已知S(Ci)∩S(C6)≠ф,i=1,2,...,5,S(Ci)∩S(Ci+1)≠ф,i=1,2,3,4,S(C5)∩S(C1)≠ф,问至少安排_____天才能考完这6门课程。
问题解答:
1.做完该题,对图的点线关系,有了进一步的了解:
无向图中的度是指该点的边数。
完全图概念如下https://zhidao.baidu.com/question/458296742266886405.html:
任意一个具有n个结点的无向简单图,其边数小于等于n*(n-1)/2;我们把边数恰好等于n*(n-1)/2的n个结点的无向图称为完全图。
最多4度,需5个点,最多边数C(5,2)=10。思考过程如下:
最后答案至少11个顶点
2.该题看似挺难,但结果是可以预计的,最多排6天,那就会很有信心做这道题,因为结果肯定是在1天到6天之间。
C6与所有课程都有交集,故C6单独排一天;交集第二多的是C5,C5与C4、C1冲突;C5排一天,C2或C3都可以与C5排一天,以排C2为例;C3与C4冲突,故C3与C1排一天;剩下C4单独排一天。上述思想布局如下:
C6;C5 C2;C3 C1;C4
还有其它类似排法,结果都是至少安排4天。
5.第十届(NOIP2004)
问题:
1.75名儿童到游乐场去玩。他们可以骑旋转木马,坐滑行铁道,乘宇宙飞船。已知其中20人这三种东西都玩过,55人至少玩过其中的两种。若每样乘坐一次的费用是5元,游乐场总共收入700,可知有 名儿童没有玩过其中任何一种。
2.已知a, b, c, d, e, f, g七个人中,a会讲英语;b会讲英语和汉语;c会讲英语、意大利语和俄语;d会讲汉语和日语;e会讲意大利语和德语;f会讲俄语、日语和法语;g会讲德语和法语。能否将他们的座位安排在圆桌旁,使得每个人都能与他身边的人交谈?如果可以,请以“a b”开头写出你的安排方案: 。
问题解答:
一度怀疑做的是普及组的题,翻出普及组,提高组试卷,才发现真是提高组,这年这两题是真的简单,小学生奥数应该能做的。
1.由题意得:
20人玩过三种东西,35人(55-20=35)只玩过其中两种。
20*5*3+35*5*2+x*5*1=700
x=10人只玩过其中一种,
剩下75-20-55-10=10人没玩过任何一种。
2.按题意排:
a(英)b(英汉)d(汉日)f(日俄法);排到目前比较简单
剩下:c(英意俄) e(意德) g(德法)
经观察c摆在a左边,上述顺序变为
c(意俄英)a(英)b(英汉)d(汉日)f(日俄法)
剩下:e(意德) g(德法)
经观察e摆在c左边,上述顺序变为
e(意德)c(意俄英)a(英)b(英汉)d(汉日)f(日俄法)
剩下: g(德法)
经观察e摆在c左边,上述顺序变为
g(德法)e(意德)c(意俄英)a(英)b(英汉)d(汉日)f(日俄法)
因ab开头,故答案为:
abdfgec
6.第十一届(NOIP2005)
问题:
1. 将数组{32, 74, 25,53, 28, 43, 86, 47}中的元素按从小到大的顺序排列,每次可以交换任
意两个元素,最少需要交换次。
2. 取火柴游戏的规则如下:一堆火柴有N根,A、B两人轮流取出。每人每次可以取1根或
2 根,最先没有火柴可取的人为败方,另一方为胜方。如果先取者有必胜策略则记为1,
先取者没有必胜策略记为0。当N分别为100,200,300,400,500时,先取者有无必
胜策略的标记顺序为(回答应为一个由0和/或1组成的字符串)。
问题解答:
1.最开始用快速排序做了一遍,但不放心,用自己的思路又做了一遍,发现结果是一致的。
方法一:快速排序
32 74 25 53 28 43 86 47
32 28 25 53 74 43 86 47 (交换74 28)
25 28|32|53 74 43 86 47 (交换32 25)
25 28|32|53 47 43 86 74 (交换74 47)
25 28|32|4347|53|86 74 (交换53 43)
25 28|32|4347|53|74 86 (交换86 74)
方法二:从结果出发,与结果对应位置相同的元素不动,交换最少的元素:
25 28 32 43 47 53 74 86
32 74 25 53 28 43 86 47
25 74 32 53 28 43 86 47(交换32 25)
25 74 32 43 28 53 86 47(交换53 43)
25 28 32 43 74 53 86 47(交换74 28)
25 28 32 43 47 53 86 74(交换74 47)
25 28 32 43 47 53 74 86(交换86 74)
有没有直接稳妥地方法,原理性的???
2.一度觉得该题,天马行空,考点在哪。当然,出发点是从头开始,思路全无。后转变思考角度,重结尾开始思考,在纸上写写画画,找到了思路。
核心思路:假定A是先取者,只要最后一轮轮到A剩下1或2根火柴,A就能获胜,以此为基础,向前推导。
A 1 2
B 3
A 4 5
B 6
A 7 8
B 9
A 10 11
B 12
A 13 14
B 15
A 16 17
B 18
通过上述推理,能得出规律:
N=100最初阶段
A 97 98
B 99
A 100 101
故A有必胜策略
N=200最初阶段
A 196 197
B 198
A 199 200
故A有必胜策略
N=300最初阶段
A 295 296
B 297
A 298 299
B 300
故A无必胜策略
N=400最初阶段
A 397 398
B 399
A 400 401
故A有必胜策略
N=500最初阶段
A 496 497
B 498
A 499 500
故A有必胜策略
答案:11011
这篇关于NOIP 提高组 初赛 三、问题求解 习题集(二)NOIP2000-NOIP2005的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!