本文主要是介绍蓝桥杯备赛 day 1 —— 递归 、递归、枚举算法(C/C++,零基础,配图),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
🌈前言
📁 枚举的概念
📁递归的概念
例题:
1. 递归实现指数型枚举
2. 递归实现排列型枚举
3. 递归实现组合型枚举
📁 递推的概念
例题:
斐波那契数列
📁习题
1. 带分数
2. 反硬币
3. 费解的开关
📁 总结
🌈前言:

这篇文章主要是准备蓝桥杯竞赛同学所写,为你更好准备蓝桥杯比赛涉及的算法知识点。不知道你是否苦恼于不知算法从何学起,苦恼于网上资料稀少,或者复杂难懂,这篇文章就是帮助这部分同学的。
这篇文章会将C平滑过度到C++,如果你只学过C语言的基本语法,也没必要担心不合适,涉及到的C++知识点会进行详细讲解。
📁 枚举的概念:
很多问题都可以" 暴力解决 " —— 不用太多脑筋,把所有可能性全部列举出来,然后一一市实验。尽管这样的方法显得很“笨”,但常常是行之有效的。
——《 算法竞赛入门经典(第2版) 》
简单的理解就是,列举出所有可能性,逐个实验,合适就留下,不合适就丢弃,看下一个,直到列举完全部数据。
这里为什么讲解枚举呢,因为在递归和递推的很多题中,常常结合枚举法,所以我们先讲解其概念,方便接下里更好的讲解递归和递推。
在算法竞赛中,对于大多数人来说,其实并不需要关注算法的优化和鲁棒性(健壮性),只需要AC(通过)即可,所以,在实际比赛中,往往通过暴力枚举的方法就可以获得大部分的分数,所以打好递归和枚举的基础,非常重要。
📁递归的概念:
递归的思想就是,将一个大问题化解成一个个子问题,直到化解成我们简单理解计算的数。放在C/C++语言中就是,1. 函数自己调用自己;2. 必须有函数调用结束条件;3. 每次调用越来越接近这个条件。
这个概念相信大家在C语言学习阶段都有学习过,所以我们简单提一下,我们通过例题来更好的理解。当然,如果你感觉一开始很难理解,这很正常,多看几遍思路,照着敲一遍,自己在写一遍(注意这里就不能照着超了,即便错了,也要自己调试,超过15分钟后依旧没思路再来看)。如果感觉头痛,休息一下,再回来敲代码,坚持不放弃就是胜利。
📁 例题:
我们先给出原题,如果你有思路,可以自己先写一遍。其次,在展示 思路,最后展示代码。
1. 递归实现指数型枚举
92. 递归实现指数型枚举 - AcWing题库
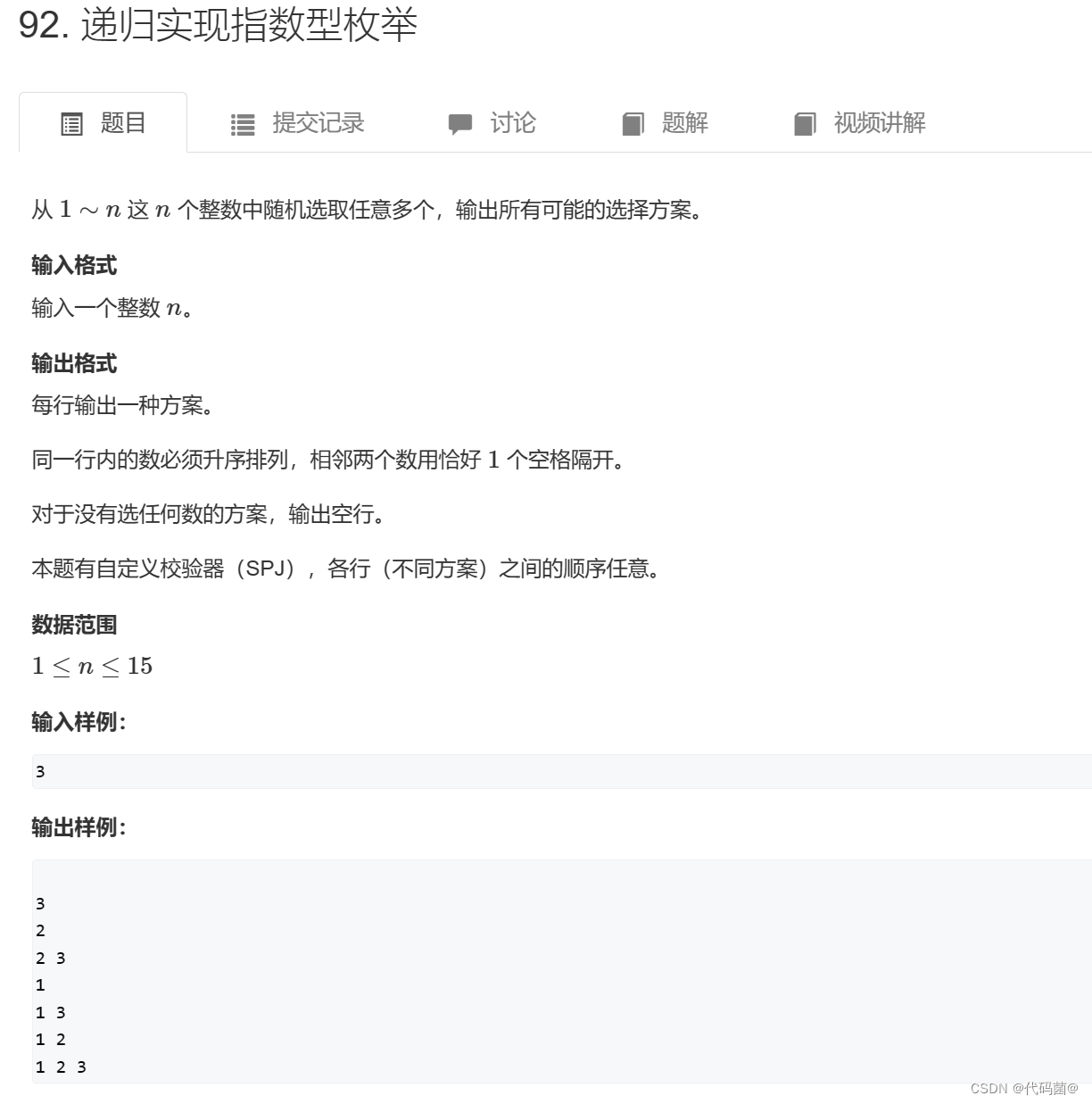
解题思路:
我们先创建一个数组,有N+1 个元素,我们使用下标1 ~ N 表示每个数,如果这个数被选择,放如数字1;如果没有被选择,就放入2。最后打印1~N被选择的数。
//引入C语言标准头文件stdio.h ,包含printf 和 scanf函数
//引入C语言标准头文件string.h ,包含字符串 和 内存 函数
#include <cstdio>
#include <cstring>//包含函数cin , cout 类似于 scanf 和 printf
#include <iostream>//C++STL算法,部分算法的使用
#include <algorithm>using namespace std;const int N = 15; //数组开辟的多一点,方便操作。int n;int st[N]; //每个数的状态,0代表未知 1代表选取 2代表未选取//u是下标
void dfs(int u)
{if (u > n){for (int i = 1;i <= n;i++){if(st[i] == 1)printf("%d ", i);}puts("");return;}st[u] = 1; //未选取dfs(u + 1);st[u] = 0; //还原现场,删掉也可以,下面会重置st[u] = 2; //选取dfs(u + 1);st[u] = 0; //还原现场}int main()
{cin >> n;dfs(1);return 0;
}2. 递归实现排列型枚举
94. 递归实现排列型枚举 - AcWing题库
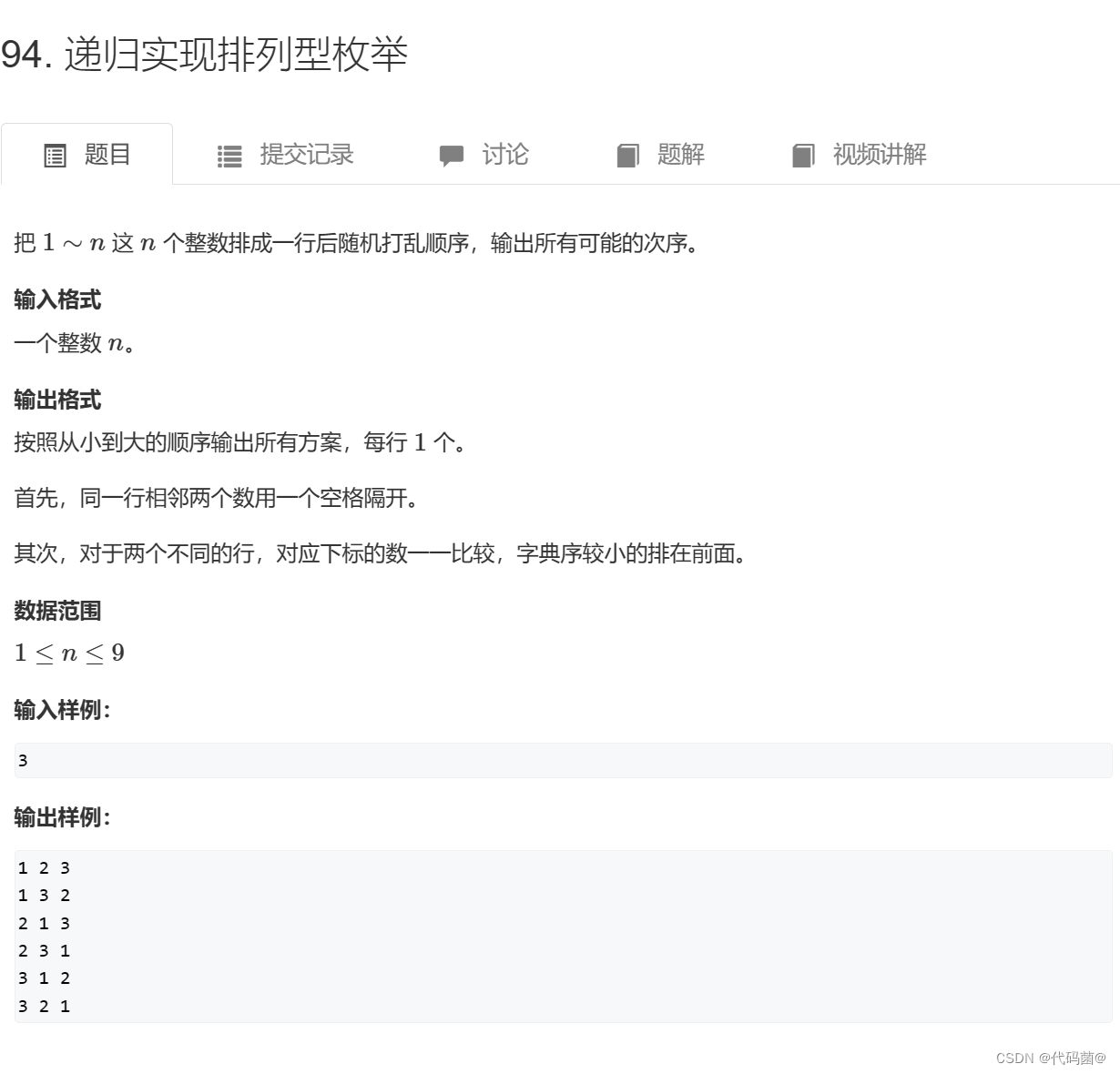
解题思路:
这里我们可以沿用上一个题解的思路,不过有了一点延伸。之前我们是对每个数进行枚举,选择或是不选择。
现在,我们对每个位置进行枚举,枚举出一个没有被选择的数,直到最后一个位置枚举结束,打印。
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>using namespace std;const int N=10; //为了方便理解,下标从1开始int n;
int stu[N]; //每个位置
bool used[N]; //每个数的状态,选择就是 true,没选择就是 false//u就是下标,代表哪一个位置
void dfs(int u)
{if (u > n){for (int i = 1;i <= n;i++){printf("%d ", stu[i]);}puts("");}for (int i = 1;i <= n;i++){if (!used[i]){stu[u] = i;used[i] = true;//递归到下一位置dfs(u + 1);//恢复现场used[i] = false;}}
}int main()
{cin >> n;dfs(1);return 0;
}3. 递归实现组合型枚举

解题思路:
什么组合呢,就是不管顺序,例如,{1,2,3} 和 {1,3, 2}若果是排列的话,就是不同的排列;如果是组合的话,就是同一个组合。
字典序是什么呢,例如 ab 和 ac 的ab字典序较小,比较的就是ASCII码值;abc 和 ab的字典序,ab在前面。
介绍了上面两个内容,已经有了做题的基础。其实这题也是非常好做的,就是排列型枚举的衍生,可以阅读样例,其实有一种规律就是,每一个位置的数据都比他前一个数据大,也就是我们从小到大依次枚举,得到的就是一个字典组较小的在前的组合。
1. 在每个位置枚举未出现的数字;
2. 每个位置的数据都比前一个位置的数据大
这里我们可以进行一个优化,例如,3个位置从1~3中进行组合,如第一个数是2 或者 3 就没必要枚举了,因为没有2 和 3 后面的数不能够填满剩余2 个位置。
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>using namespace std;const int N = 25;int n;
int m;
int ways[N]; //每个位置的数据,存放到数组ways中//u就是下标,start就是比前一个位置的数据大的那个数据
void dfs(int u,int start)
{//这里进行了优化,例如样例中,4和5放在第一个位置就没必要往下枚举了if (n - start < m - u){return;}//枚举完了m个位置,进行打印if(u > m){for(int i =1;i<=m;i++){printf("%d ",ways[i]);}puts("");return ;}//在每个位置上进行枚举操作,枚举没有出现的数字,并保持有序for(int i=start;i<=n;i++){ways[u] = i;dfs(u + 1 ,i + 1);}
}int main()
{cin>>n>>m;dfs(1,1); //下标从1开始;start = 1,即从1开始枚举return 0;
}📁 递推的概念:
递归的理解就是,先求出小问题,再由小问题求出大问题。下面就用斐波那契数列作为讲解,第三项就是前两项求和。
📁例题:
斐波那契数列
#include <iostream>using namespace std;int n,fib[50];int main(){cin >> n;feibo[0]=0;feibo[1]=1;for(int i=2;i<n;++i) fib[i]=fib[i-1]+fib[i-2];for(int i=0;i<n;++i) printf("%d ",fib[i]);return 0;
}📁习题:
1. 带分数
1209. 带分数 - AcWing题库
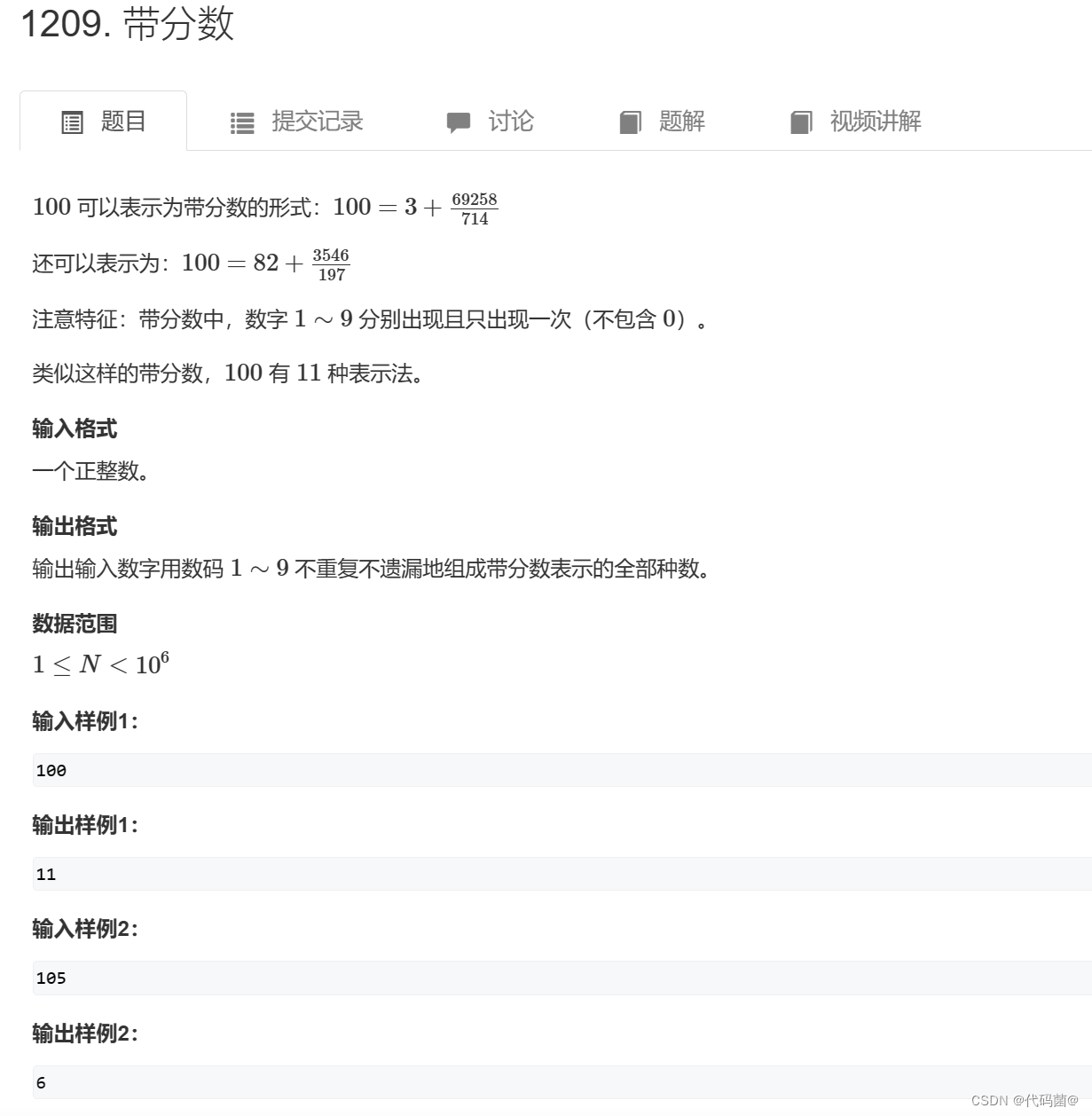
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>using namespace std;const int N = 20;bool used[10];int num;
int ans;bool check(int a, int c)
{long long b = num * (long long)c - a * c;if (!a || !b || !c){return false;}bool backup[N];memcpy(backup, used, sizeof used);while (b){int i = b % 10;b /= 10;if (!i ||backup[i]){return false;}backup[i] = true;}for (int i = 1;i < 10;i++){if (!backup[i]){return false;}}return true;
}void dfs_c(int u,int a, int c)
{if (u > 9){return;}if (check(a, c)){ans++;}for (int i = 1;i <= 9;i++){if (!used[i]){used[i] = true;dfs_c(u + 1, a, c * 10 + i);used[i] = false;}}
}void dfs_a(int u,int a)
{if (a >= num){return;}if (a){dfs_c(u, a, 0);}for (int i = 1;i <= 9;i++){if (!used[i]){used[i] = true;dfs_a(u + 1, a * 10 + i);used[i] = false;}}
}int main()
{cin >> num;dfs_a(0,0);cout << ans;return 0;
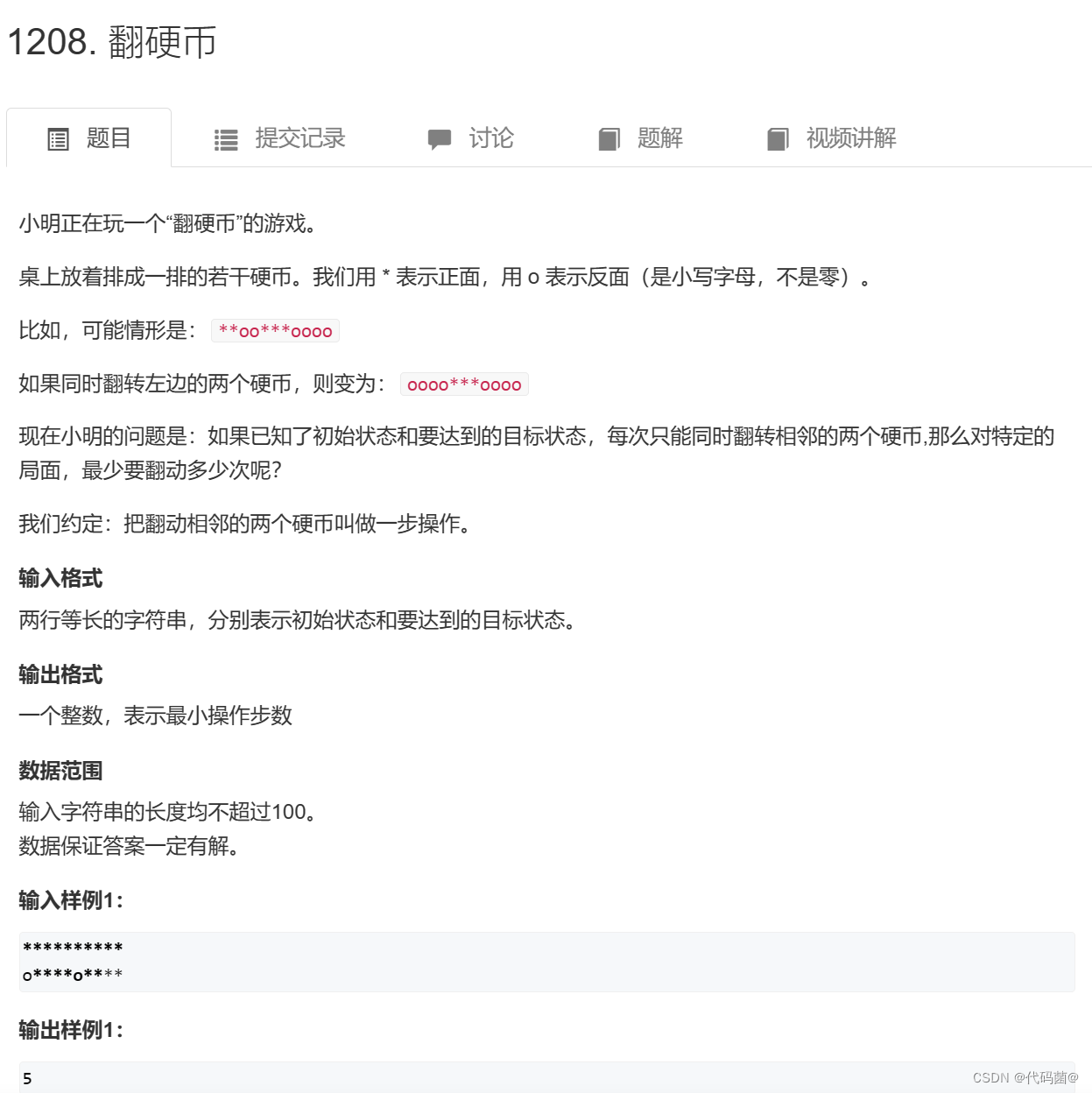
}2. 翻硬币
1208. 翻硬币 - AcWing题库
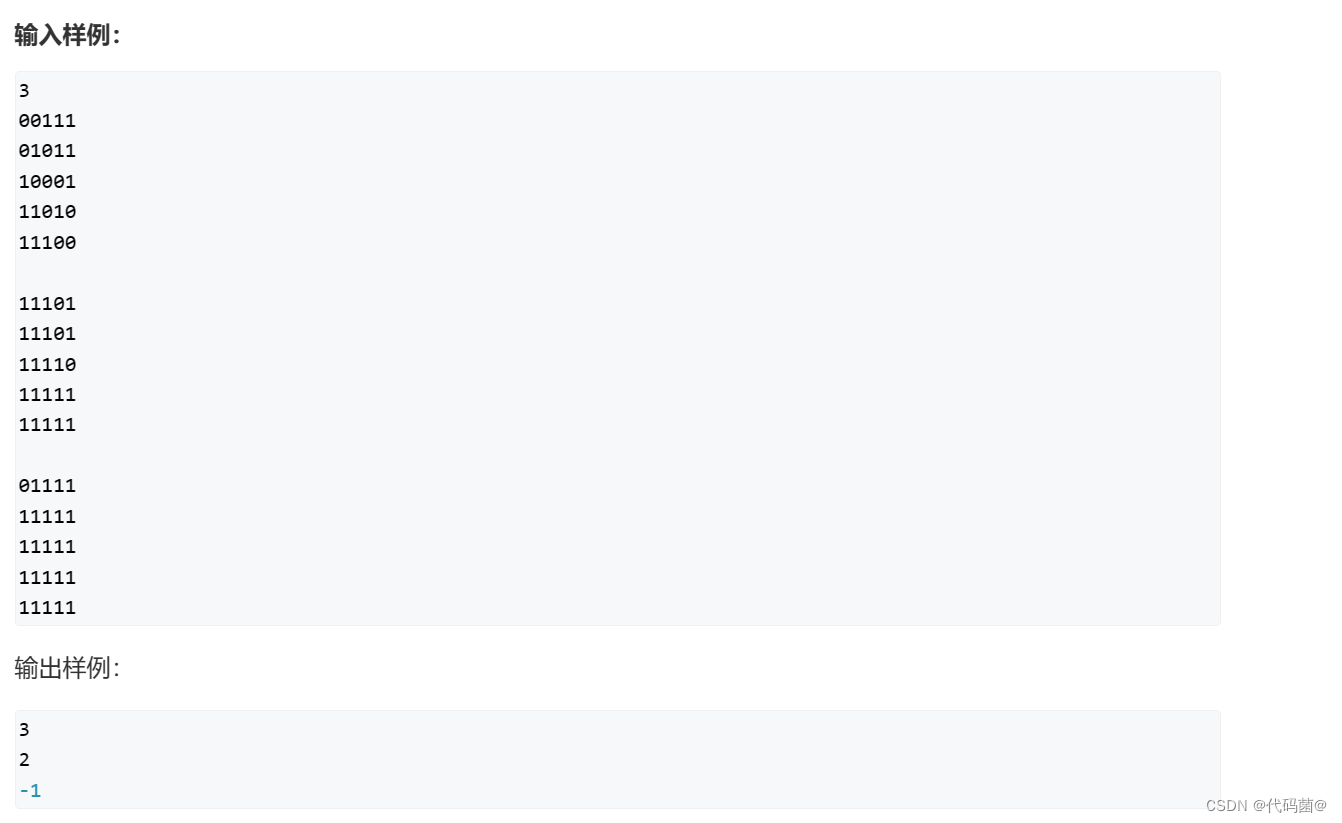
3. 费解的开关
95. 费解的开关 - AcWing题库

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>using namespace std;char g[6][6], back[6][6];
int T;
int dx[5] = { -1,0,1,0,0 }, dy[5] = { 0,1,0,-1,0 };void turn(int x,int y)
{for (int i = 0;i < 5;i++){int a = x + dx[i];int b = y + dy[i];if (a < 0 || a >= 5 || b < 0 || b >= 5){continue;}g[a][b] ^= 1;}
}int main()
{cin >> T;while (T--){//对每一行进行输入for (int i = 0;i < 5;i++){cin >> g[i];}int ret = 10;//枚举第一行的操作for (int op = 0;op < 32;op++){int step = 0;memcpy(back, g, sizeof g);//对第一行进行操作for (int i = 0;i < 5;i++){if (op >> i & 1){step++;turn(0, i);}}//对第2 - 4 行进行操作for (int i = 0;i < 4;i++)for (int j = 0;j < 5;j++){if (g[i][j] == '0'){step++;turn(i + 1, j);}}//对最后一行进行检查bool dark = false;for (int i = 0;i < 5;i++){if (g[4][i] == '0'){dark = true;break;}}if (!dark)ret = min(step, ret);memcpy(g, back, sizeof g);}if (ret > 6)ret = -1;cout << ret << endl;}return 0;
}
📁 总结:
以上,我们就对递归、递推和枚举在蓝桥杯中的知识点进行了讲解,并针对性的讲解了例题,当然这也只是帮你更好的理解这些算法知识,想要学好算法,还需要不断地刷题练习,这里推荐到洛谷,acwing等网站进行练习,比如你看完了这篇文章,做回了例题习题,就可以上这些网站进行想应的练习。

这篇关于蓝桥杯备赛 day 1 —— 递归 、递归、枚举算法(C/C++,零基础,配图)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!