本文主要是介绍团伙挖掘算法整理,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
团伙挖掘技术调研
文章目录
- 1. 模块度优化
- Louvain
- Leiden
- 2. 标号传播
- 3. DeepWalk
- 经典的Deepwalk
- GEMSEC
- 4. 频谱聚类
- 经典的频谱聚类
- 5. Multi-view clustering
- 经典的multi-view clustering
- GMC
- 6. GNN
- DMoN
- SDCN
- O2MAC
- LGNN
- 7. Matrix Factorization
- 经典的NMF (Nonnegative Matrix Factorization)
- NSED
- MNMF
- DANMF
- 8. Generative Model
- CommunityGAN
- Supplementary
- Ego-splitting Framework
1. 模块度优化
Louvain
Fast unfolding of communities in large networks[J]. Journal of
statistical mechanics: theory and experiment, 2008, 2008(10): P10008.
Pre-knowledge
模块度
度量社区划分优劣的指标,直观上表示某社团划分状态下,社团内部连边数量与该划分下随机连边数量的差值。
计算公式如下:
Q = 1 2 m ∑ i , j [ A i j − k i k j 2 m ] δ ( c i , c j ) Q=\frac{1}{2m}\sum_{i,j}[A_{ij}-\frac{k_ik_j}{2m}]\delta(c_i,c_j) Q=2m1i,j∑[Aij−2mkikj]δ(ci,cj)
模块度越大,说明社团内部联系越紧密,社团间联系越稀疏,社团划分效果越好
Overview
Louvain:启发式。两个步骤,①move nodes;②aggregate

Shortcoming
bad connected

Leiden
Paper:From Louvain to Leiden: Guaranteeing Well-connected Communities, 2019
C++ Reference
innovations
- 增加refine步骤→保证了社团的连接性(Louvain缺陷)
- 减少节点扫描次数→节省训练时间
Overview
Leiden: 三个步骤,①move nodes;②refine;③aggregate

- 增加refine步骤:
设move nodes后的划分为P,仍然按照P进行社团划分,
但对每个community内重新进行节点间的merge(半随机),merge出的划分记为 P r e f i n e d P_{refined} Prefined。(通常 P r e f i n e d P_{refined} Prefined会将P的每个社区细化为多个子社区。)根据 P r e f i n e d P_{refined} Prefined进行下一步的aggregate
假设图d中的红色社团bad-connected,由于内部有两个节点,后续仍然有机会划分到不同的社团中去,保证了最终的社团都well-connected。 - 减少节点扫描次数
Louvain对每个节点进行扫描,计算模块度增益,而Leiden只对邻居节点发生变化的节点进行扫描和计算,从而提高了运算效率。
Experiment
- dataset:DBLP、Amazon、IMDB、Live Journal、Web of Science、Web UK
- results:max modularity
2. 标号传播
Pre-knowledge
Soft label
对每个样本,保留它属于每个类类别的概率,而非互斥(最终用max确定类别)
Overview
Algorithm1(unsupervised):
初始化每个节点一个唯一标号
每个节点根据邻居中频率最高的标签,更新自身标签
迭代直至稳定
Algorithm2 (semi-supervised):
1. 首先计算权重矩阵,节点i,j之间的权重: w i , j = e x p ( − ∣ ∣ x i − x j ∣ ∣ 2 2 2 σ 2 ) w_{i,j}=exp(-\frac{||x_i-x_j||_2^2}{2\sigma^2}) wi,j=exp(−2σ2∣∣xi−xj∣∣22)
2. 概率转移矩阵P: P i j = P ( i → j ) = w i j ∑ k = 1 n w i k P_{ij}=P(i→j)=\frac{w_{ij}}{\sum_{k=1}^nw_{ik}} Pij=P(i→j)=∑k=1nwikwij
3. 构造标签矩阵F∈n*c,n为样本点数,c为社团数。
对于labeled data,对应标签列取1,其余取0;对于unlabeled data,随机取一个1。
4. 执行标签传播:重复以下两个步骤直至F收敛
- F=PF
- 重置F中labeled data的标签为真实标签
Algorithm3(异步更新):
同步更新遇到二分图容易产生振荡,因此提出异步更新策略
在Algorithm2的基础上,后更新的节点基于前面节点标签更新后的标签矩阵
此时受节点更新顺序影响大,一般采取随机顺序
3. DeepWalk
经典的Deepwalk
Pre-knowledge
word2vec
文本embedding的方法。
使用双层神经网络,输入层是word的one-hot编码,隐层权重W是embedding的训练目标,输出层Hierarchical Softmax作超大规模分类器。
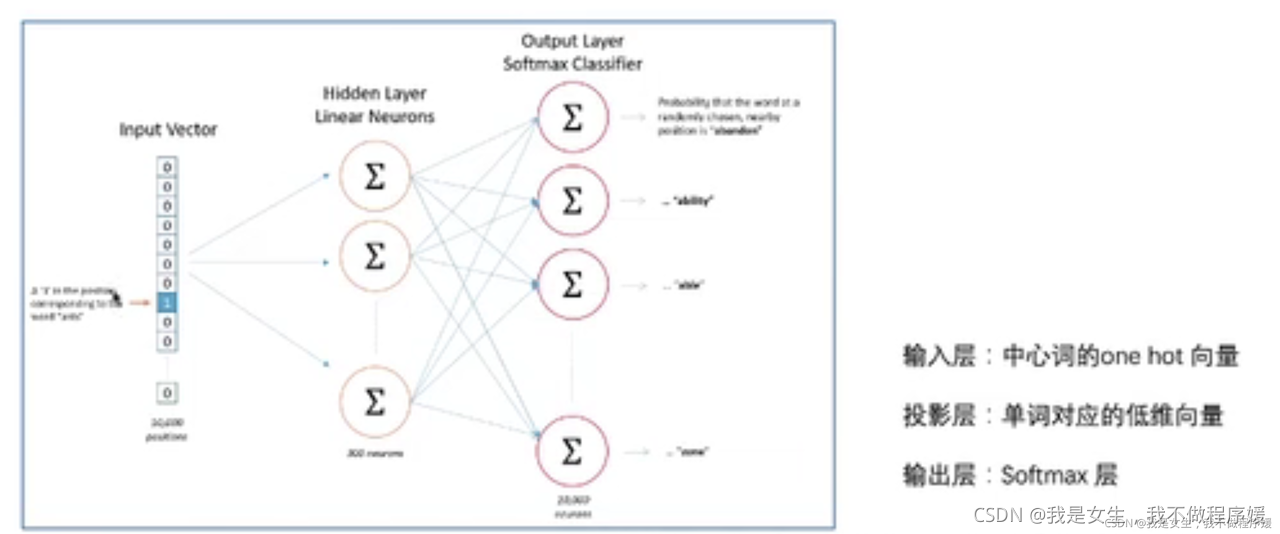
Overview
将Word2Vec应用于图,使用图中节点与节点的共现关系来学习节点的向量表示。
1. 构建同构网络,从网络中的每个节点开始分别进行Random Walk 采样,得到局部相关联的训练数据,将离散的网络节点表示成向量化;

RandomWalk是一种可重复访问已访问节点的深度优先遍历算法。给定当前访问起始节点,从其邻居中随机采样节点作为下一个访问节点,重复此过程,直到访问序列长度满足预设条件。
- 对采样数据进行SkipGram训练,最大化节点共现;使用Hierarchical Softmax来做超大规模分类的分类器。(同Word2vec)
GEMSEC
Paper:Graph Embedding with Self-Clustering, 2019
Python Reference
innovations
- 在DeepWalk基础上,增加目标函数项,使节点embedding分布在聚类中心周围;
- 引入平滑正则项来迫使具有高度重叠邻域的节点对有相似的节点表示。
Overview
-
基于DeepWalk,加入聚类相关的目标函数
f:节点的embedding,μ:聚类中心 第一项(公式中的Embedding
cost)为使用了Softmax的节点共现概率函数化简后的形式,主要作用是使得采样的序列中同一个窗口内的节点的表示向量具有相似的表示。
第二项(公式中的Clustering cost)为聚类的目标函数(类似Kmeans),旨在最小化节点与最近的聚类中心的距离。 -
引入平滑正则项来迫使具有高度重叠邻域的节点对有相似的节点表示
 w:两节点邻居重叠度,即
w:两节点邻居重叠度,即

Experiment
- dataset:Facebook,Deezer
- results:mean modularity和f1-score
(Smooth是应用了正则项平滑的方法,2是应用了二阶相似性的方法)
4. 频谱聚类
经典的频谱聚类
Pre-knowledge
如何构造相似度矩阵S
- ε-邻近法
使用欧氏距离计算相似性。
设定阈值ε,若相似性≥ε,则 s i j s_{ij} sij=ε;否则 s i j s_{ij} sij=0。
此方法计算出两点间的相似度要么是ε,要么是0,丧失了很多数据间相似性信息,适用于无权图。 - 近邻法(常用的稀疏相似矩阵)
使用高斯相似度进行度量 s i , j = e x p ( − ∣ ∣ x i − x j ∣ ∣ 2 2 2 σ 2 ) s_{i,j}=exp(-\frac{||x_i-x_j||_2^2}{2\sigma^2}) si,j=exp(−2σ2∣∣xi−xj∣∣22)。
设定近邻数k,对每个样本的k近邻,使用高斯相似度;非k近邻, s i j s_{ij} sij=0。 为避免造成不对称,有2种方法:两点互为k近邻才取 s i j s_{ij} sij>0;两点有一点是对方的k近邻即取 s i j s_{ij} sij>0。 - 全连接法
可选高斯核函数、多项式核函数、Sigmoid核函数等方法度量。
所有点之间的权重都大于0。
Overview
输入:样本集D=(𝑥1,𝑥2,…,𝑥𝑛),聚类个数k
输出: 簇划分𝐶(𝑐1,𝑐2,…𝑐k).
1. 样本相似度矩阵S:
我们有n个样本,计算样本的相似度矩阵,记为S。
2. 邻接矩阵A:
对每个样本点,取其k近邻作为其邻居节点,构造邻接矩阵A。
即如果i是j的k近邻且j是i的k近邻,则 A i , j = S i , j A_{i,j}=S_{i,j} Ai,j=Si,j ,否则 A i , j = 0 A_{i,j}=0 Ai,j=0
3. 度矩阵D:
D是一个对角阵,对角元是每个节点的度,其余元素为0.
4. 非标准化的拉普拉斯矩阵:
L=D-A
有一条重要的性质:拉普拉斯矩阵的0特征值重数r等于其对应的图中的连通分量的个数。
5. 求出 L 的特征值,取最小的k个特征值
求其对应的特征向量,组成一个n*k的矩阵,即降维后的特征矩阵,每行对应一个样本点。
6. 按行对标准化后的特征向量矩阵进行聚类(如k-means)
Shortcoming
- 谱聚类对相似图和聚类参数的选择非常敏感;
- 谱聚类适用于均衡分类问题,即簇之间点的个数差别不大,对于簇之间点的个数相差悬殊的问题不适用。
5. Multi-view clustering
经典的multi-view clustering
Overview
对同一数据集从多种角度(使用不同特征/加入不同噪声等)构造多个视图,所有视图生成一个融合图,再进行基于图的聚类
Shortcommings
- 没有考虑不同视图的重要性差异(权重问题)
- 需要额外的聚类方法(如k-means)
- 各视图和融合图的构造彼此孤立
GMC
Paper: GMC: Graph-based Multi-view Clustering, 2019
Matlab Reference
innovations
combines Multi-View clustering with spectral clustering
- 权重自动确定;
- 通过施加拉普拉斯秩约束,自动生成聚类结果
- 每个视图和融合图的构造improves simultaneously
Overview

Cost function:

- 第一项和第二项:由data matrix(X)计算similarity- induced graph(SIG),X是用向量表示样本点的矩阵,SIG是相似矩阵的稀疏表示(以增强鲁棒性),用于优化各视图的相似矩阵的表示;
- 第三项:U是融合图表示,w是权重,第三项用于优化融合图的表示,使其更接近每个视图;
- 第四项:拉普拉斯秩约束,根据拉普拉斯矩阵的性质,添加该约束后融合图U表示的图有c个连通分量,即被自动聚类为c类。F={f1,f2,…fc},由U的特征向量组成,每一列是聚类中心的向量表示
Output:
求出U,其包含c个连通分量,即c个聚类
Experiment
-
6. GNN
Pre-knowledge
GNN与GCN
假设图中有N个节点(node),每个节点都有自己的D维特征,这些节点的特征组成一个N×D维的矩阵X,然后各个节点之间的关系也会形成一个N×N维的矩阵A(邻接矩阵)(adjacency matrix)。
- 图神经网络(GNN):用多维向量(节点属性)表示图节点,学习过程将节点之间的关系加入节点向量。
- 图卷积神经网络(GCN):改进的GNN。
- input:X与A
- output:每个节点的embedding,既包含节点属性信息,又包含了关系信息(即相邻节点表示相似)。
DMoN
Paper:Graph Clustering with Graph Neural Networks, 2020
Code Reference
innovations
applying GCN to clustering by introducing modularity
Overview
聚类矩阵: C = s o f t m a x ( G C N ( A ~ , X ) ) C=softmax(GCN(\widetilde{A},X)) C=softmax(GCN(A ,X))
损失函数:

第一项:模块度的相反数;
第二项:F-范数,用于避免聚类方法将所有点划分到同一类别的天然倾向。无监督
Experiment
- dataset:Cora、Citeseer、Pubmed、Amazon PC、Amazon Photo、Coauthor CS、Coauthor PHY
- results:average cluster conductance、modularity、NMI、F1-score

SDCN
Paper: Structural Deep Clustering Network, 2020
Python Reference
Pre-knowledge
KL散度
即相对熵,用来度量两种概率分布P和Q之间的差异。
在聚类问题中,常用Q表示当前聚类结果下的实际分布;
P表示squared and normalized后的分布(此时的分布具有更高的confidence,即同簇节点分布更加集中);
通过优化KL散度,使得Q朝着P的方向优化,以达到data分布在聚类中心附近的效果
Innovations
- combines GCN with DNN
- Introduce KL divergence
Overview
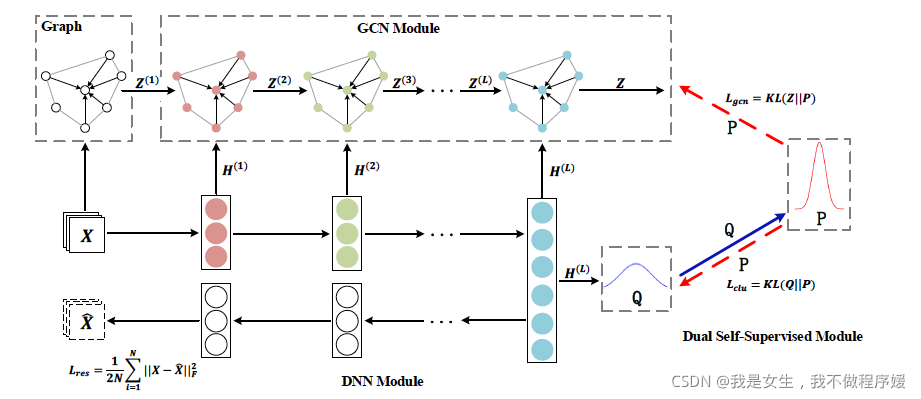
Input of GCN: raw data(X) and KNN graph(A)(or original graph);学习节点之间的高阶关系
Input of DNN(autoencoder): raw data;降维表示节点属性
KL divergence:使得data分布在聚类中心附近
联系:①GCN(Z)每轮迭代时融入DNN(H)
②dual self-supervised module:两个神经网络使用统一目标函数,使两个神经网络向着同一目标(优化结构表示并生成聚类)优化
Output:Z即最终的soft assignment
Experiment
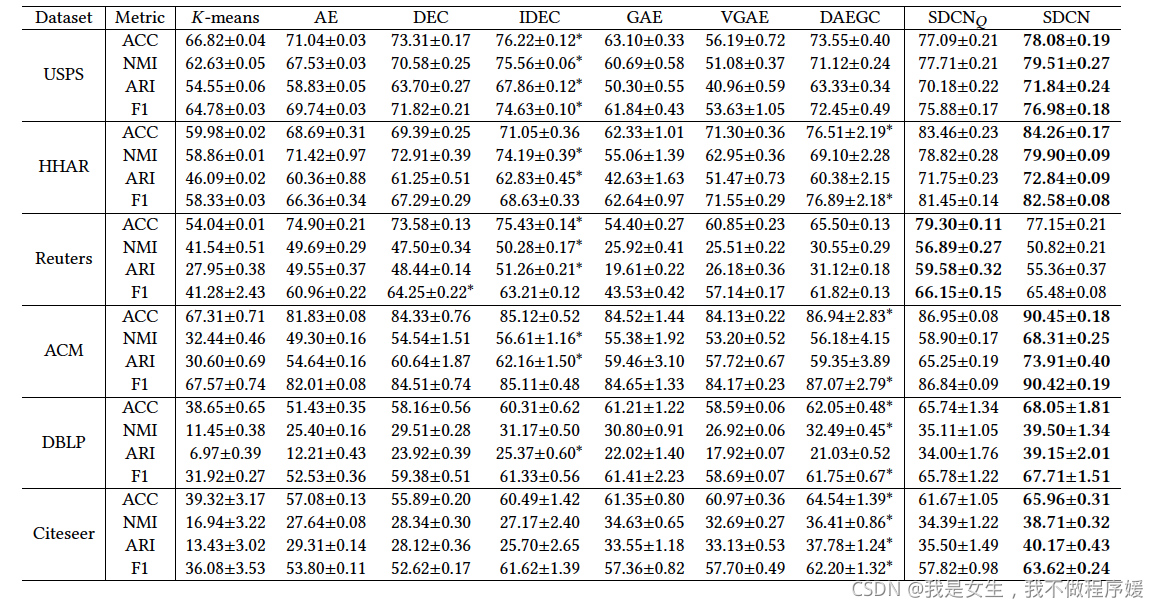
- dataset:USPS、HHAR、Reuters、ACM、DBLP、Citeseer.
- results:ACC、NMI、ARI、F1
O2MAC
Paper: One2Multi Graph Autoencoder for Multi-view Graph Clustering, 2020
Python Reference
innovation
combines graph deep learning with multi-view clustering
Overview

- For each A with X: input a GCN; use k-means and modularity to select A* with the most information to be the input
- one-encoder: Input A* and X into a 2-layer GCN
- Multi-decoder: use Z to reconstruct all views A1…Am
- Self-training clustering:加入KL散度的目标函数,使embedding data分布在聚类中心附近
Experiment
- dataset:ACM、DBLP、IMDB
- results:ACC、F1、NMI、ARI

LGNN
Supervised Community Detection with Line Graph Neural Networks, 2019
Python Reference
Pre-knowledge
线性图神经网络
LG(线图):将图中的边作为节点,相邻边相连,构造双向图

Innovation
使用线图神经网络(LGNN)进行社团检测
Overview

更新策略:(G and L(G) respectively)
其中,O为高阶(power)邻接矩阵;x、z为G的点向量;y、w为L(G)的点向量,θ为待训练参数。ρ为非线性激活函数。
可以表示features,可以overlap
输出:接一个softmax,表示某节点属于各个社团的概率
Loss function:

其中 o i , c o_{i,c} oi,c表示节点i属于社团c的概率。
Experiment
- dataset:Amazon、DBLP、YouTube
- results:node classification accuracy

7. Matrix Factorization
经典的NMF (Nonnegative Matrix Factorization)

input:A(feature×sample);
output:Z(community×sample),隐因子、列代表community;行代表node;值代表可能性; W:basis matrix
Shortcomings
- 不能保证W的稀疏性
- Comsuming for new samples
NSED
Paper: A Non-negative Symmetric Encoder-Decoder Approach for Community Detection,2017
Python Reference
Innovation
通过对称矩阵分解保证:
- 每个节点只属于一个或少数几个社团
- 更容易求解
Overview
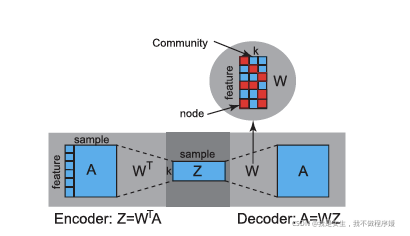

对称矩阵分解保证了W的软正交性
软正交性+非负性 → 稀疏性:每个节点只属于一个或少数几个社团
Experiment
- dataset:Amazon、DBLP
- Results:
1. Synthetic networks:
NMI:normalized mutual information
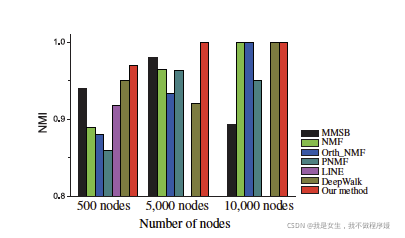
- Real world networks:


MNMF
Community Preserving Network Embedding, 2017
Python Reference
Pre-knowledge
网络节点的相似性
一阶相似性:即两节点直接相似性,可用边的权重表示;
二阶相似性:间接相似性,即两节点的邻接节点的相似性,可用邻接矩阵中两节点向量的余弦相似度表示
innovations
同时引入了节点结构和社区结构进行两个矩阵分解。

S:网络的节点结构,由一阶相似性和二阶相似性组成,
M:basis matrix;
U:节点表示矩阵,n×m,用m维向量(隐因子)表示一个节点;
H:网络的社区结构,n×k,每行一个1,其余都是0,表示节点属于社区;only disjoint
C:社区表示矩阵,k×m,用m维向量(隐因子)代表一个社团;
Q = t r ( H T B H ) Q=tr(H^TBH) Q=tr(HTBH),模块度。
Experiment
- dataset:WebKB、Political blog network、Facebook network、four socialnetworks
- Results:聚类和分类

Shortcomings
- 矩阵分解开销太大;
- only disjoint communities
DANMF
Paper: Deep Autoencoder-like Nonnegative Matrix Factorization for Community Detection, 2019
Python Reference
Innovation
deep learning in encoder and decoder to better learn the complicated structures
Overview
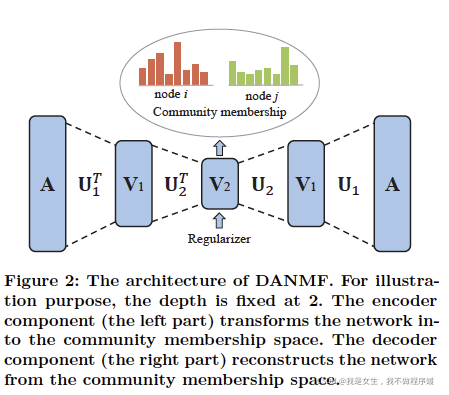
A ≈ U 1 U 2 . . . U p V p A≈U_1U_2...U_pV_p A≈U1U2...UpVp
V p ≈ U p T . . . U 2 T U 1 T A V_p≈U^T_p...U^T_2U^T_1A Vp≈UpT...U2TU1TA
Experiment
- dataset:
1. non-overlapped community detection:Email,Wiki,Cora,Citeseer,Pubmed
2. overlapped communities:synthetic networks
- results:Better than A Non-negative Symmetric Encoder-Decoder Approach for Community Detection(NSED) and Community Preserving Network Embedding(MNMF)
3. non-overlapped community:
ARI:Adjusted Rand Index
NMI:Normalized Mutual Information
ACC:Accuracy



4. Overlapping:
ONMI:Overlapping NMI
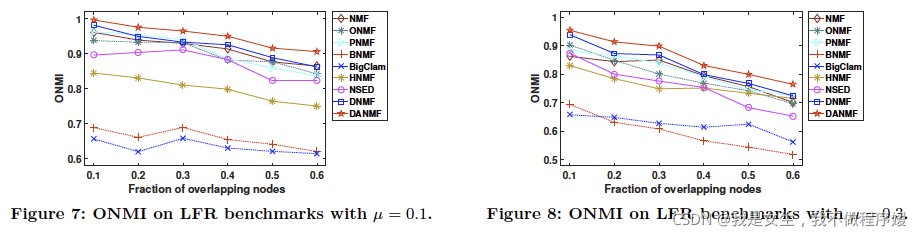
Shortcomings
harder to train
8. Generative Model
CommunityGAN
Paper: CommunityGAN: Community Detection with Generative Adversarial Nets, 2019 Python
Reference
Pre-knowledge
AGM
Affiliation Graph Model,一个典型的AGM网络包括(V, C, M, {Pc})四个参数,
V:节点; C:社团; M:节点的embedding,用非负矩阵表示节点对每个社团的隶属度(概率); {Pc}:两点间存在连边的概率。
由AGM网络可以等价地生成新图G’,节点u, v之间存在连边的概率为:
p ( u , v ) = 1 − e x p ( − F u T ⋅ F v ) p(u,v)=1-exp(-F_u^T·F_v) p(u,v)=1−exp(−FuT⋅Fv)


Pre-knowledge
GAN
Generative Adversarial Network,to optimize such embedding

Pre-knowledge
clique
a subset of vertices of an undirected graph ,where every two distinct vertices are adjacent.
innovations
combines AGM(representation) with GAN(learning method)
本文不仅考虑两个节点间的关系(as AGM does),还考虑motif(clique)
Overview
Input and output:

- 本文不仅考虑两个节点间的关系(as AGM does),还考虑motif(clique)
文章证明community和clique之间是正相关关系
上式扩展为“对于节点集v{1,…m},能形成clique的概率”: - combines AGM(representation) with GAN(learning method)
Train GAN via AGM’s representation
G用于生成最像clique的节点子集,D判别上述节点是否为clique;
D和G利用AGM的公式,不断学习更新Fv,计算得到p用以衡量学习结果。
最终得到各节点的Fv(c维)。大于一定阈值则认为属于该社团。
Experiment- dataset:Amazon、YouTube、DBLP
- result:

Supplementary
-
限制网络范围:极大连通子图
严格意义上,团伙挖掘不等于社区发现,我们的目标团伙实际上只是复杂网络中的一小部分节点。
为提高运算效率和准确度,可以首先使用极大连通子图将团伙挖掘限定在较小的范围内。 -
算法适用场景

-
从embedding的角度
feature作边的算法需要结合其他算法,进行不基于业务字段的特征提取和选择,并加权为一个维度构造网络图的边;
内含embedding的算法则不需要 -
从重叠与否的角度——重叠转化为非重叠的framework
Ego-splitting Framework
Ego-splitting Framework: from Non-Overlapping to Overlapping Clusters, 2018
Python Reference
Overview
transfer overlapping networks to non-overlapping networks
1. 重构网络:对每个node,只考虑其邻居组成的网络,根据连通性构建该节点的一或多个映像

- 进行非重叠社团划分(可使用任意non-overlapping clustering algorithm,文中使用label propagation)
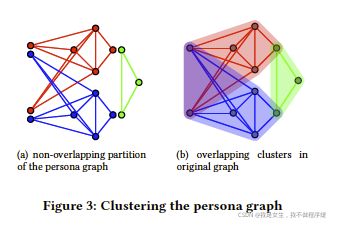
Experiment
- dataset:Amazon、DBLP、Live Journal、orkut、friendster、clueweb12
- results:F1、NMI、running time


这篇关于团伙挖掘算法整理的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








