本文主要是介绍王小草【机器学习】笔记--EM算法,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
标签(空格分隔): 王小草机器学习笔记
EM算法的英文全称是Expectation Maximization Algorithm,也就是求期望最大化,也就是我们常说的目标函数求最大值的算法。EM算法,直观的说,就是有一堆未知的数据(比如一些特征值),这些数据可能来自于不同的类别,而你想知道的是每一个数据都来自于哪个类别,并且知道来自于这个类别的概率是多少。而在EM算法看来,每一个类别中的数据必然服从了某个固有的分布(如二项分布,正态分布等),只要寻找它密度函数的参数,就能知道数据的分布,所以EM使用了极大似然估计的方法去估计了各个分布的参数,从而进行了无监督地聚类。
本文首先会回顾和复习一下EM算法中要涉及到的知识:Jensen不等式和最大似然估计;
然后介绍EM算法,并且会用混合高斯GMM来作为例子用EM算法求解。
最后,会给出一些实现EM算法的python实例。
1. 回顾
1.1 回顾Jensen不等式
Jensen不等式这个名字有点陌生,但是如果眼睁睁地看到这个不等式,你肯定会觉得特别特别熟悉,并且鼻尖传来阵阵数学考试卷的味道,它会出现在选择题填空题或者后面的大分推导题中。万万没想到,今天还会在那么重要的算法中遇到。
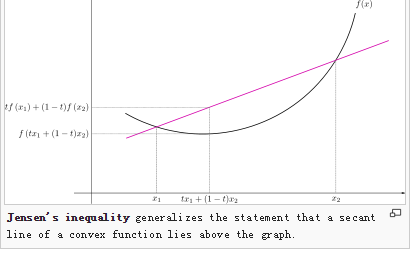
假设有两个变量x1,x2,有一个函数f(),并且函数f是凸函数,那么就肯定有以下不等式成立:
f(θx1 + (1-θ)x2) <= θf(x1) + (1-θ)f(x2)
在二维坐标中表示如下
同理,若有多个x,多个θ,只要满足f是凸函数,并且
θ1,θ2,…θk >= 0;且θ1+θ2+…+θk = 1
那么下面不等式肯定成立:
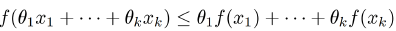
上面讲的是离散型的变量,针对连续型的变量,Jesen不等式也是成立的。
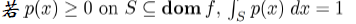

 中θ是随机变量,分别与xi相乘后相加,其实就是在求x的期望值,那么以上任何形式的不等式,都可以表示成如下:
中θ是随机变量,分别与xi相乘后相加,其实就是在求x的期望值,那么以上任何形式的不等式,都可以表示成如下:

1.2 回顾K-means算法
之所以要在EM算法中回顾K-means,是因为在迭代k-means中其实就是不断取均值点求期望的过程,于EM迭代求最大化期望类似。
先初始选择k个簇中心,然后根据各个样本点到中心的距离来分割,再对分割后的类找到这个类中所有样本点的中心点(均值点)作为新的簇中心,然后再进行聚类,再找新的中心,如此循环,直到满足终止条件而停止。
这里,通过各个样本的均值来确定新的中心点其实就是在求期望,其过程的大致思路其实与我们接下去要讲的EM算法是类似的。
k-means能够非常方便得将样本分成若干簇,但是由一个巨大的问题是,我们无法知道这个样本点属于这个簇的概率,我们只知道属于或不属于的布尔值,如此一来,就没那么好玩了。
那么如果想知道概率的话,就得去找到与样本分布最接近的概率分布模型,要得到概率分布模型,就得先将模型中的参数估计出来。EM算法所实现的就是这个功能。
2.最大似然估计求参数
2.1 小引子
先来看一个简单的例子。
简单的例子一般都离不开抛硬币来。
假设我们现在不知道抛硬币出现正反面的概率,然后设每抛一次出现正面的概率是p,这个p是我们想求得的。
现在我做一个实验,将硬币抛是10次,然后记录结果为:正正反正正正反反正正。
最大似然估计就是去求出现以上这10次结果的概率最大时候,去估计p的概率。
因为每次抛硬币是一个独立事件,所以每一次抛硬币的概率是可以相乘的,于是以上10次结果发生的概率可以写成:
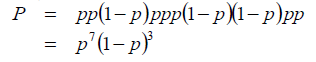
要求的P最大时p的值,其实就是对以上等式求目标函数最优化的过程,最后可以求出p=0.7。
当然,你肯定会义正言辞地说,不对!抛硬币的概率谁不知道呢,正反两面出现的概率都是0.5呀!
这是因为我们这个实验中只抛了10次,样本量太小存在的误差会偏大,如果抛100次,1000次,10000次,样本中正反两面出现的次数会越来越趋于1:1,那么求出来的p值肯定也会更接近与0.5了。
当然,你肯定还会义正言辞得说,可是这个极大似然估计有什么用吗,抛硬币的概率我本来就知道。嗯,对,抛硬币只是一个例子。假如我收集了上海9月份30天的天气数据,想知道9月份的上海下雨的概率p有多大;再假如我记录了今年我从东昌路上2号线有没有座位的数据,想知道上车后有座位的概率p是多少;再假如我有所有进入购物网站的行为数据样本,想知道首次进来的人会购买下单的概率;再假如二号店若推出新品促销的广告,用户看到会点击进入的概率…等等。这些概率我想你应该不知道,但作为商家也许会非常渴望知道。
2.2 二项分布的最大似然估计
抛硬币其实是一个二项分布,它有两个值,概率分别为p和1-p。
假设投掷N次硬币,出现正面朝上次数是n,反面朝上的次数是N-n。
并且设正面朝上的概率是p。
现在使用似然函数来求目标函数的最优化,为了计算方便,我们将函数取对数来求最大值,成为“对数似然函数”。
目标函数如下:
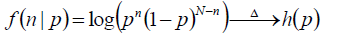
对目标函数中的p求导数,最后得到p = n/N
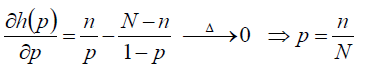
以上就是用最大似然函数估计二项分布参数的过程。
2.3 高斯分布的最大似然估计
现在我们来看一看高斯分布。
若给定一组样本X1,X2,X3…Xn,已知他们是来自于高斯分布N(μ,σ),即符合均值为μ,标准差为σ的正太分布。要根据这些样本点的分布去估计这个正态分布的参数μ,σ。
1.首先,要知道高斯分布的概率密度函数:
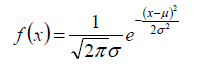
里面有两个参数,分别就是μ,σ。也是我们要求的参数。
2.要得到样本点那样分布的概率,假设每个样本都是独立的,所有总的概率就是每个样本的概率的乘积:
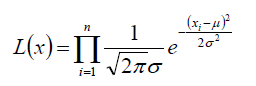
3.对上面的等式进行对数似然函数的化简:

4.得到化简后的目标函数:
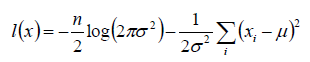
现在就是对这个目标函数求最大值时的参数μ,σ的值
5.将目标函数分别对参数μ,σ进行求导,就能求出μ,σ的公式:
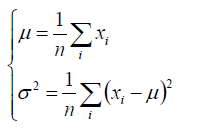
以上就是用最大似然函数估计高斯分布参数的过程。
3.EM算法
经过了冗长的铺垫终于到了本文的重点了–EM算法。在讲EM算法乏味难懂的定理前,我们先用高斯混合模型来走一遍它的参数估计
3.1 直观理解猜测GMM的参数估计
已知一个学校的所有学生的身高样本(X1,X2,X3…Xn),并且男生和女生都分别服从N(μ男,σ男)和N(μ女,σ女)的高斯分布。目的是要求出μ男,σ男,μ女,σ女这四个参数。
来来来理一下这个题目,与上文中的例子不同了,现在同时有两个高斯分布混合在一起,我们要去求出两个高斯分布各自的均值与标准差参数。那么问题来了…我怎么知道某个样本属于男高斯还是女高斯啊,现在我们只知道所有的身高值,并不知道这些身高背后的性别呀。恩恩,这是一个混合高斯模型,简称GMM(随机变量是由2个高斯分布混合而成)。在GMM中,有一个隐藏的随机变量我们没法看到,那就是性别,因为无法知道性别的概率,也就无法知道某个样本属于哪个高斯分布的了。所以这个隐藏的概率π男,π女也是我们需要估计的,它表示某个样本属于某个高斯分布的概率。
将上面的例子扩展地表示出来:随机变量X是由K个高斯分布混合而成,取各个高斯分布的概率为π1,π2,π3…πk;第i个高斯分布的均值为μi,方差为Σi。若观测到随机变量X的一系列样本X1,X2,X3…Xn,试估计参数π,μ,Σ。
1.建立目标函数
同样的,我们使用对数似然函数来建立目标函数
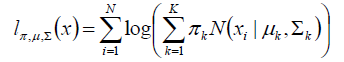
由于对数函数里面又有加和,无法直接用求导解方程的方法来求最大值。为了解决这个问题,接下来分两步走。
2.第一步:估计数据来自哪个组(也就是说来自哪个高斯分布)
首先我们根据经验随便给定π,μ,Σ的先验值。
然后求r(i,k),表示,样本i 由高斯分布k生成的概率。公式如下:
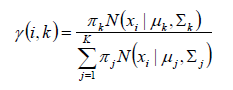
根据这个公式,我们可以求得样本X1分别属于K1,K2,K3..的概率
3.第二步:估计每个高斯分布中的参数
对于高斯分布k来说,它说生成的点可看成是{r(i,k)*xi|i-=,1,2,3..N},就是所有原来的样本点乘以它属于高斯分布k的概率,从而得到了新的样本点,这些样本点应是服从高斯分布k的。因此高斯分布k的样本个数不再是原来的N,而是所有样本属于它的概率的加和: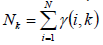
同理,π,μ,Σ都可以因此重新计算:
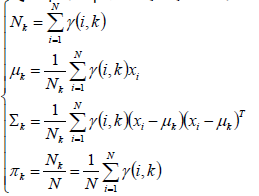
4.重复第一步,第二步
我们用先验的π,μ,Σ计算出来新
这篇关于王小草【机器学习】笔记--EM算法的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








