本文主要是介绍读算法霸权笔记01_数学杀伤性武器,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
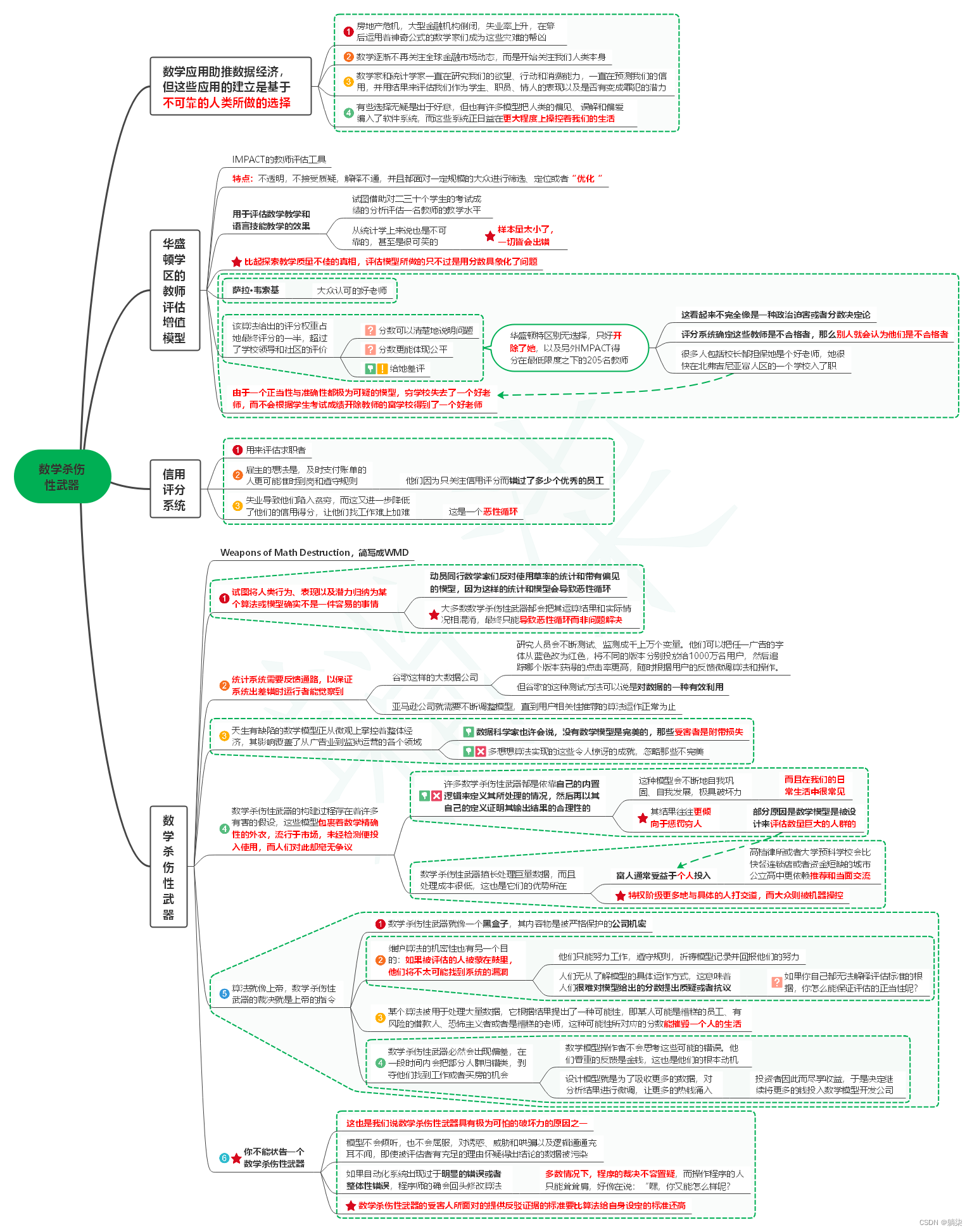
1. 数学应用助推数据经济,但这些应用的建立是基于不可靠的人类所做的选择
1.1. 房地产危机,大型金融机构倒闭,失业率上升,在幕后运用着神奇公式的数学家们成为这些灾难的帮凶
1.2. 数学逐渐不再关注全球金融市场动态,而是开始关注我们人类本身
1.3. 数学家和统计学家一直在研究我们的欲望、行动和消费能力,一直在预测我们的信用,并用结果来评估我们作为学生、职员、情人的表现以及是否有变成罪犯的潜力
1.4. 有些选择无疑是出于好意,但也有许多模型把人类的偏见、误解和偏爱编入了软件系统,而这些系统正日益在更大程度上操控着我们的生活
2. 华盛顿学区的教师评估增值模型
2.1. IMPACT的教师评估工具
2.2. 特点:不透明,不接受质疑,解释不通,并且都面对一定规模的大众进行筛选、定位或者“优化“
2.3. 用于评估数学教学和语言技能教学的效果
2.3.1. 试图借助对二三十个学生的考试成绩的分析评估一名教师的教学水平
2.3.2. 从统计学上来说也是不可靠的,甚至是很可笑的
2.3.2.1. 样本量太小了,一切皆会出错
2.4. 比起探索教学质量不佳的真相,评估模型所做的只不过是用分数具象化了问题
2.5. 萨拉·韦索基
2.5.1. 大众认可的好老师
2.6. 该算法给出的评分权重占她最终评分的一半,超过了学校领导和社区的评价
2.6.1. 分数可以清楚地说明问题
2.6.2. 分数更能体现公平
2.6.3. 给她差评
2.6.4. 华盛顿特区别无选择,只好开除了她,以及另外IMPACT得分在最低限度之下的205名教师
2.6.4.1. 这看起来不完全像是一种政治迫害或者分数决定论
2.6.4.2. 评分系统确定这些教师是不合格者,那么别人就会认为他们是不合格者
2.6.4.3. 很多人包括校长都担保她是个好老师,她很快在北弗吉尼亚富人区的一个学校入了职
2.7. 由于一个正当性与准确性都极为可疑的模型,穷学校失去了一个好老师,而不会根据学生考试成绩开除教师的富学校得到了一个好老师
3. 信用评分系统
3.1. 用来评估求职者
3.2. 雇主的想法是,及时支付账单的人更可能准时到岗和遵守规则
3.2.1. 他们因为只关注信用评分而错过了多少个优秀的员工
3.3. 失业导致他们陷入贫穷,而这又进一步降低了他们的信用得分,让他们找工作难上加难
3.3.1. 这是一个恶性循环
4. 数学杀伤性武器
4.1. Weapons of Math Destruction,简写成WMD
4.2. 试图将人类行为、表现以及潜力归纳为某个算法或模型确实不是一件容易的事情
4.2.1. 动员同行数学家们反对使用草率的统计和带有偏见的模型,因为这样的统计和模型会导致恶性循环
4.2.2. 大多数数学杀伤性武器都会把其运算结果和实际情况相混淆,最终只能导致恶性循环而非问题解决
4.3. 统计系统需要反馈通路,以保证系统出差错时运行者能觉察到
4.3.1. 谷歌这样的大数据公司
4.3.1.1. 研究人员会不断测试、监测成千上万个变量。他们可以把任一广告的字体从蓝色改为红色,将不同的版本分别投放给1000万名用户,然后追踪哪个版本获得的点击率更高,随时根据用户的反馈微调算法和操作。
4.3.1.2. 但谷歌的这种测试方法可以说是对数据的一种有效利用
4.3.2. 亚马逊公司就需要不断调整模型,直到用户相关性推荐的算法运作正常为止
4.4. 天生有缺陷的数学模型正从微观上掌控着整体经济,其影响覆盖了从广告业到监狱运营的各个领域
4.4.1. 数据科学家也许会说,没有数学模型是完美的,那些受害者是附带损失
4.4.2. 多想想算法实现的这些令人惊讶的成就,忽略那些不完美
4.5. 数学杀伤性武器的构建过程存在着许多有害的假设,这些模型包裹着数学精确性的外衣,流行于市场,未经检测便投入使用,而人们对此却毫无争议
4.5.1. 许多数学杀伤性武器都是依靠自己的内置逻辑来定义其所处理的情况,然后再以其自己的定义证明其输出结果的合理性的
4.5.1.1. 这种模型会不断地自我巩固、自我发展,极具破坏力
4.5.1.1.1. 而且在我们的日常生活中很常见
4.5.1.2. 其结果往往更倾向于惩罚穷人
4.5.1.2.1. 部分原因是数学模型是被设计来评估数量巨大的人群的
4.5.2. 数学杀伤性武器擅长处理巨量数据,而且处理成本很低,这也是它们的优势所在
4.5.2.1. 富人通常受益于个人投入
4.5.2.1.1. 高档律所或者大学预科学校会比快餐连锁店或者资金短缺的城市公立高中更依赖推荐和当面交流
4.5.2.2. 特权阶级更多地与具体的人打交道,而大众则被机器操控
4.6. 算法就像上帝,数学杀伤性武器的裁决就是上帝的指令
4.6.1. 数学杀伤性武器就像一个黑盒子,其内容物是被严格保护的公司机密
4.6.2. 维护算法的机密性也有另一个目的:如果被评估的人被蒙在鼓里,他们将不太可能找到系统的漏洞
4.6.2.1. 他们只能努力工作,遵守规则,祈祷模型记录并回报他们的努力
4.6.2.2. 人们无从了解模型的具体运作方式,这意味着人们很难对模型给出的分数提出质疑或者抗议
4.6.2.2.1. 如果你自己都无法解释评估标准的根据,你怎么能保证评估的正当性呢?
4.6.3. 某个算法被用于处理大量数据,它根据结果提出了一种可能性,即某人可能是糟糕的员工、有风险的借款人、恐怖主义者或者是糟糕的老师,这种可能性所对应的分数能摧毁一个人的生活
4.6.4. 数学杀伤性武器必然会出现偏差,在一段时间内会把部分人群归错类,剥夺他们找到工作或者买房的机会
4.6.4.1. 数学模型操作者不会思考这些可能的错误。他们看重的反馈是金钱,这也是他们的根本动机
4.6.4.2. 设计模型就是为了吸收更多的数据,对分析结果进行微调,让更多的热钱涌入
4.6.4.2.1. 投资者因此而尽享收益,于是决定继续将更多的钱投入数学模型开发公司
4.7. 你不能状告一个数学杀伤性武器
4.7.1. 这也是我们说数学杀伤性武器具有极为可怕的破坏力的原因之一
4.7.2. 模型不会倾听,也不会屈服,对诱惑、威胁和哄骗以及逻辑通通充耳不闻,即使被评估者有充足的理由怀疑得出结论的数据被污染
4.7.3. 如果自动化系统出现过于明显的错误或者整体性错误,程序师的确会回头修改算法
4.7.3.1. 多数情况下,程序的裁决不容置疑,而操作程序的人只能耸耸肩,好像在说:“嘿,你又能怎么样呢?
4.7.4. 数学杀伤性武器的受害人所面对的提供反驳证据的标准要比算法给自身设定的标准还高
这篇关于读算法霸权笔记01_数学杀伤性武器的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








