本文主要是介绍五分钟学完DBSCAN算法,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
基础概念
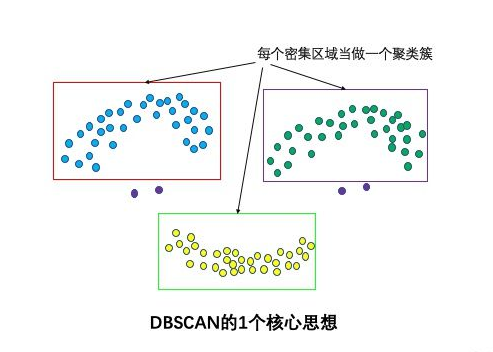
邻1个核心思想:基于密度,依据密度的连通性分析增长聚类
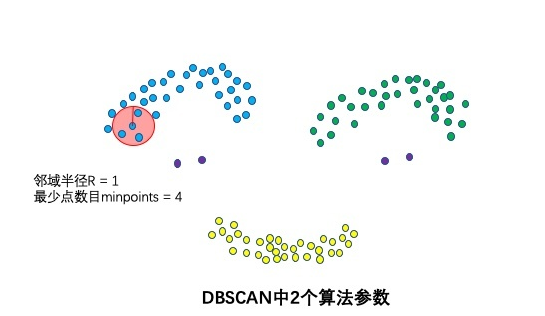
2个算法参数:邻域半径R和最少点数目minpoints
这两个算法参数实际可以刻画什么叫密集——当邻域半径R内的点的个数大于最少点数目minpoints时,就是密集。
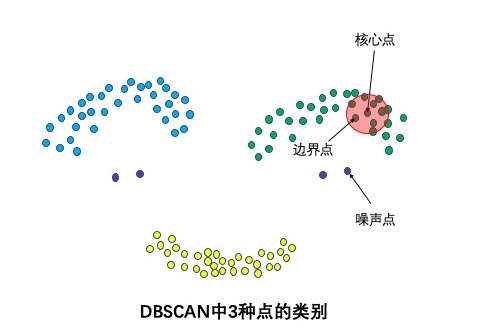
3种点的类别:核心点,边界点和噪声点
邻域半径R内样本点的数量大于等于minpoints的点叫做核心点。不属于核心点但在某个核心点的邻域内的点叫做边界点。既不是核心点也不是边界点的是噪声点。
4种点的关系:密度直达,密度可达,密度相连,非密度相连
密度直达(直接密度可达): 给定一个对象集合 D,如果 p在q 的邻域内,而 q 是一个核心对象(核心点),则我们说对象 p 从对象 q 出发是直接密度可达的。
ps:根据定义,出发的点必须是核心点,如果P为核心点,Q在P的R邻域内,那么称P到Q密度直达。任何核心点到其自身密度直达,密度直达不具有对称性,如果P到Q密度直达,那么Q到P不一定密度直达。
密度可达:如果存在核心点P2,P3,……,Pn,且P1到P2密度直达,P2到P3密度直达,……,P(n-1)到Pn密度直达,Pn到Q密度直达,则P1到Q密度可达。密度可达也不具有对称性。其中Q为非核心点。
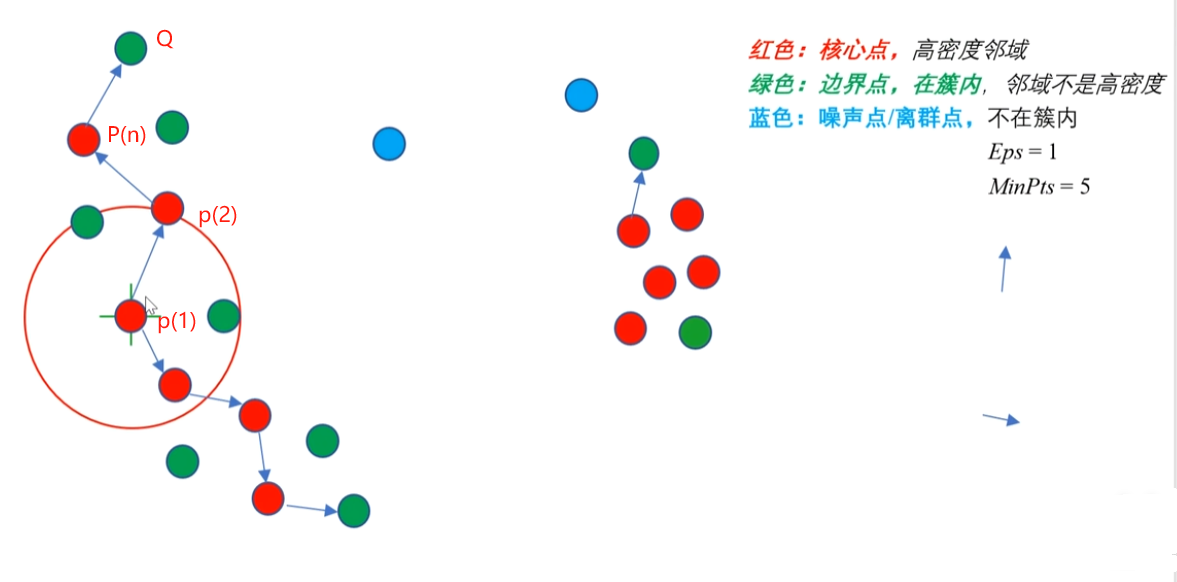
解释:p1密度直达p2,p2直达p(n),红色点都是核心点,但是Q是非核心点,所以p1密度直达Q。
如下图所示,如果存在核心点S(图中箭头指向的点),使得S到Q1和Q2都密度可达,则Q1和Q2密度相连。密度相连具有对称性,如果Q1和Q2密度相连,那么Q2和Q1也一定密度相连。密度相连的两个点属于同一个聚类簇。
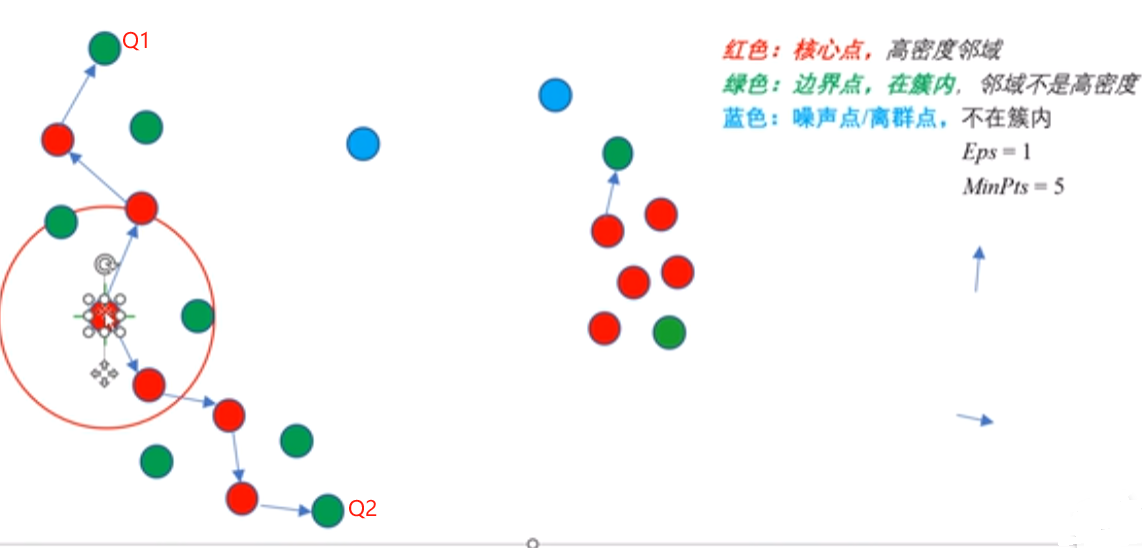
如果两个点不属于密度相连关系,则两个点非密度相连。非密度相连的两个点属于不同的聚类簇,或者其中存在噪声点。
算法实例
下面给出一个样本数据集,如表 1 所示,并对其实施 DBSCAN 算法进行聚类,取 Eps=3,MinPts=3。
数据集中的样本数据在二维空间内的表示如图 3 所示。
图 3 直接密度可达和密度可达示意
第一步,顺序扫描数据集的样本点,首先取到 p1(1,2)。
1)计算 p1 的邻域,计算出每一点到 p1 的距离,如 d(p1,p2)=sqrt(1+1)=1.414。
2)根据每个样本点到 p1 的距离,计算出 p1 的 Eps 邻域为 {p1,p2,p3,p13}。
3)因为 p1 的 Eps 邻域含有 4 个点,大于 MinPts(3),所以,p1 为核心点。
4)以 p1 为核心点建立簇 C1,即找出所有从 p1 密度可达的点。
5)p1 邻域内的点都是 p1 直接密度可达的点,所以都属于C1。
6)寻找 p1 密度可达的点,p2 的邻域为 {p1,p2,p3,p4,p13},因为 p1 密度可达 p2,p2 密度可达 p4,所以 p1 密度可达 p4,因此 p4 也属于 C1。
7)p3 的邻域为 {p1,p2,p3,p4,p13},p13的邻域为 {p1,p2,p3,p4,p13},p3 和 p13 都是核心点,但是它们邻域的点都已经在 Cl 中。
8)P4 的邻域为 {p3,p4,p13},为核心点,其邻域内的所有点都已经被处理。
9)此时,以 p1 为核心点出发的那些密度可达的对象都全部处理完毕,得到簇C1,包含点 {p1,p2,p3,p13,p4}。
第二步,继续顺序扫描数据集的样本点,取到p5(5,8)。
1)计算 p5 的邻域,计算出每一点到 p5 的距离,如 d(p1,p8)-sqrt(4+1)=2.236。
2)根据每个样本点到 p5 的距离,计算出p5的Eps邻域为{p5,p6,p7,p8}。
3)因为 p5 的 Eps 邻域含有 4 个点,大于 MinPts(3),所以,p5 为核心点。
4)以 p5 为核心点建立簇 C2,即找出所有从 p5 密度可达的点,可以获得簇 C2,包含点 {p5,p6,p7,p8}。
第三步,继续顺序扫描数据集的样本点,取到 p9(9,5)。
1)计算出 p9 的 Eps 邻域为 {p9},个数小于 MinPts(3),所以 p9 不是核心点。
2)对 p9 处理结束。
第四步,继续顺序扫描数据集的样本点,取到 p10(1,12)。
1)计算出 p10 的 Eps 邻域为 {p10,pll},个数小于 MinPts(3),所以 p10 不是核心点。
2)对 p10 处理结束。
第五步,继续顺序扫描数据集的样本点,取到 p11(3,12)。
1)计算出 p11 的 Eps 邻域为 {p11,p10,p12},个数等于 MinPts(3),所以 p11 是核心点。
2)从 p12 的邻域为 {p12,p11},不是核心点。
3)以 p11 为核心点建立簇 C3,包含点 {p11,p10,p12}。
第六步,继续扫描数据的样本点,p12、p13 都已经被处理过,算法结束。
我们通过这个算法,得到了3个簇和一个噪声点。
这篇关于五分钟学完DBSCAN算法的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








