Python科学计算学习：从入门到放弃系列（2）用scipy解常微分方程组（涉及解释蝴蝶效应现象）

前言

Python 科学计算，接下来重点是三个，分别是1）解微分方程，2）画图和3）数值优化。前两者是相互关联的，因为对于微分方程的求解，如果不进行绘图展示，是很难直观理解解的含义的。另外，这部分的学习，对我来说有点困难，只能一步一步，慢慢前进了。

1. 问题描述（来自教材）

现在有一组常系数微分方程组（洛伦兹吸引子，这是混沌里面的内容）

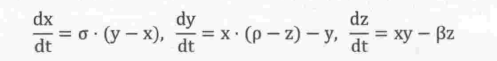
三个方程表示了粒子在空间三个方向上的速度，求解这个方程组，也就是要在给定起点 $(x_0,y_0,z_0)$ 和常数 $(\sigma ,\rho ,\beta )$ 情况下，求出一系列的坐标点 $(x_i,y_i,z_i)$ (即粒子的空间轨迹。)

敲黑板重点：上面的方程，都是一阶的，就是每个变量，只是对时间 $t$ 求一阶微分，这种情况下，才是我们今天介绍的函数能解的。如果是二阶及以上，需要进行转化才能求解(这部分内容暂时不会涉及）。

2. 解决步骤

1. 写目标函数，其返回值是待求解的常微分方程组，该函数的自变量，包括微分方程组的自变量，还有待求值的时间片，方程常数
2. 运行时间片调用 numpy.arange()，进行切片（计算机数值求解均是离散的）
3. 调用 scipy,integrate.odeint() 进行求解，返回结果应该是与t时间片对应的各个状态
4. 绘图即可展示给定时间里面的解！

3. 编程实现

3.1 实现代码

#!/usr/bin/env python
# -*- coding: utf-8 -*-
# @Date    : 2019-04-09 16:10:50
# @Author  : Promise (promise@mail.ustc.edu.cn)
# @Link    : ${link}
# @Version : $Id$from scipy.integrate import odeint  # 用from语法的，直接调用，不需要前面的包
import numpy as np
from mpl_toolkits.mplot3d import Axes3D
import pylab as pl  # pylab 和 pyplot 有相近的功能
from scipy import integrate
import matplotlib.pyplot as pltdef lorenz(w, t, p, r, b):# w 是矢量，包含（x, y, z）, 三个参数 p,r,b# 计算微分量？x, y, z = w.tolist()# 返回量是lorenz的计算公式return p*(y-x), x*(r-z)-y, x*y - b*zt = np.arange(0, 30, 0.02)  # 时间点
# 调用 ode 对 lorenz进行求解
track1 = odeint(lorenz, (0.0, 1.00, 0.0), t, args=(10.0, 28.0, 3.0))  # odeint,函数名后面的位置，是传入自定义函数的参数
track2 = odeint(lorenz, (0.0, 1.01, 0.0), t, args=(10.0, 28.0, 3.0))
print(track1)
print(track1[:, 0])  # 取出第0列的意思，因为数组的每一行分别是 x,y,z; 取第0列就是把所有x取出来# 画图fig = pl.figure()
ax = Axes3D(fig)
ax.plot(track1[:, 0], track1[:, 1], track1[:, 2], lw=1)
ax.plot(track2[:, 0], track2[:, 1], track2[:, 2], lw=1)  # 用同一个ax,说明两幅图画在同一幅图
# 最后的show()不能忘
pl.show()

3.2 运行效果

微分方程的计算机求解，本质上是把微分方程离散成差分方程（离散才是计算机的本质，就像或许量子的离散才是我们这个连续物质世界的本质，一切都是这么奇妙~）

求解过程，是以初始条件为起点，计算给定时间内每一个位置$(x,y,z)$，因此，odeint()函数，返回的是一系列数据点，如果仅是数值输出，是看不出什么规律的，只有画成上图，我们才能直观把握整个系统是如何运动的。上图两个线，是两条轨迹图。

洛伦兹吸引子是混沌理论里面的一个例子，讲的是，即使对于有确定描述的运动方程，只要初始条件有稍微的不同（如程序中，初始条件，(0.0, 1.00, 0.0) 和 (0.0, 1.01, 0.0)，仅相差0.01), 也会导致后期的运动轨迹完全不同，用大家熟悉的话来说，就是蝴蝶效应。

3.3 代码分析

1. 需要调用的程序包，照着上面程序导入即可
2. 时间分片函数，t = np.arange(0, 30, 0.02) # 时间点, 这是图中轨迹的来源，因为有这么多时间片段，才有那么多点让我们刻画轨迹
3. odeint()的调用，track1 = odeint(lorenz, (0.0, 1.00, 0.0), t, args=(10.0, 28.0, 3.0)) # odeint,函数名后面的位置，是传入自定义函数的参数, 第一个参数，是我们要求解的微分方程组对应函数的函数名（有点绕），后面的所有参数，其实都是该函数定义过程中，使用的参数，请仔细阅读上面的代码
4. odeint() 的返回值，是一个 $m$ 行 $n$ 列的矩阵，$n$ 对应我们定义的函数 $lorenz(w,t,p,r,b)$ 返回值的个数，这个例子是3个($(x,y,z)$)， 因此$n=3$； $m$行对应时间片的数量，多少片，多少行。
5. track1[:, 0], 对应第4的分析，每一列对应一个返回值，这里表示取出第0列，也就是把所有$x$的值取出来，因为要画图。

4. 总结

在Python科学计算这里，是相对简单的，只要懂得基本的求解原理，照着说明使用求解函数，就可以了。